664A - Сложный НОД

Идея задачи — GlebsHP

В этой задачи нужно было рассмотреть два случая:

1. a = b — отрезок состоит из одного числа, следовательно все числа из этого отрезка делятся на a и не делятся ни на какое число большее, чем a.
2. a < b — в этом случае НОД(a, a + 1, a + 2, ..., b) = НОД(НОД(a, a + 1), a + 2, ..., b) = НОД(1, a + 2, ..., b) = 1.

#include <bits/stdc++.h>

using namespace std;

int main() {
    string a, b;
    cin >> a >> b;

    if (a == b) cout << a;
    else cout << 1;

    return 0;
}

663A - Ребус

Идея задачи — gen

Для начала давайте определим, существует ли решение ребуса. Для этого достаточно знать только количество положительных элементов (первый элемент всегда положительный и все знаки вопроса, перед которыми стоит  + ) и количество отрицательных элементов (все знаки вопроса, перед которыми стоит  - ). Обозначим эти количества как pos и neg, тогда минимальная сумма, которую мы можем получить — это min = (1 · pos - n · neg) (все положительные вопросики заменяем на минимальное значение 1, а все отрицательные — на максимальное n), аналогично, максимальная сумма равна max = (n · pos - 1 · neg). Тогда решение существует тогда и только тогда, когда min ≤ n ≤ max.

Пусть мы определили, что решение существует, теперь будем будем постепенно заменять вопросики числами. Пусть мы уже заменили некоторый префикс вопросиков на числа и получили там сумму S, текущий вопросик имеет знак sgn ( + 1 или  - 1) и справа (но не считая текущий) осталось pos_left положительных и neg_left отрицательных элементов. Текущий элемент мы заменим на число x. Как проверить, что мы можем заменить текущий вопросик на x? Точно так же, как мы вначале определяли, существует ли решение вообще. Мы можем найти минимальную и максимальную суммы, которые мы сможем получить — min_left = (S + sgn · x + pos_left - n · neg_left) и max_left = (S + sgn · x + n · pos_left - neg_left) соответственно, тогда мы можем заменить текущий вопросик на число x, если min_left ≤ n ≤ max_left. Как найти подходящее значение x? Можно честно решить систему неравенств, а можно просто перебрать все n значений.

BONUS Пусть k — количество знаков вопроса в ребусе. Докажите, что асимптотика решения с перебором (для примера, смотрите реализацию ниже) — O(k² + n), а не O(k · n).

#include<bits/stdc++.h>

using namespace std;

char s[100];

int main() {
    int k = 0, n, pos = 1, neg = 0;
    while (true) {
        char c;
        scanf(" %c", &c);
        scanf(" %c", &c);

        if (c == '=') break;
        if (c == '+') pos++;
        if (c == '-') neg++;

        s[k++] = c;
    }

    scanf("%d", &n);

    if (pos - n * neg > n || n * pos - neg < n) {
        printf("Impossible\\n");

        return 0;
    }

    printf("Possible\\n");

    int S = 0;
    for (int i = 0; i < k; i++) {
        int sgn = 1;
        if (i > 0 && s[i - 1] == '-') sgn = -1;

        if (sgn == 1) pos--;
        if (sgn == -1) neg--;

        for (int x = 1; x <= n; x++)
            if (S + x * sgn + pos - n * neg <= n && S + x * sgn + n * pos - neg >= n) {
                printf("%d %c ", x, s[i]);

                S += x * sgn;

                break;
            }
	}

    printf("%d = %d\\n", abs(n - m), n);

    return 0;
}

662D - Международная олимпиада

Идея задачи — Alex_2oo8

Давайте посмотрим на сокращения, которые получают первые олимпиады. Первые 10 олимпиад (с 1989 до 1998 года соответственно) получают сокращение из одной цифры (IAO'9, IAO'0, ..., IAO'8) — на данный момент все одноцифренные сокращения заняты. Следующие 100 олимпиад (1999 - 2098) получат скоращение из двух цифр (так как последние две цифры у 100 подряд идущий чисел попарно различны). Аналогично, следующие 1000 олимпиад получат сокращения из трех цифр и так далее.

Теперь решим задачу в обратную сторну (по сокращению определим год). Пусть данное сокращение имеет длину k цифр, тогда мы знаем, что до нашей олимпиады прошли все олимпиады с сокращениями длины (k - 1), (k - 2), ..., 1, то есть 10^k - 1 + 10^k - 2 + ... + 10¹ = F олимпиад и наша олимпиада была одна из 10^k следующих. То есть наша олимпиада проходила в один из годов между (1989 + F) и (1989 + F + 10^k - 1), так как мы получили отрезок из 10^k подряд идущих чисел, то ровно одно число из этого отрезка будет иметь последние k цифр совпадающие с нашим сокращением, этот год и будет соответствовать нашему сокращению.

#include <bits/stdc++.h>

using namespace std;

char s[42];

int main() {
    int n;
    scanf("%d", &n);
    while (n--) {
        scanf(" %s", s);
        
        int k = strlen(s + 4), year = atoi(s + 4), F = 0, tenPow = 10;
        for (int i = 1; i < k; i++) {
            F += tenPow;
            tenPow *= 10;
        }
        
        while (year < 1989 + F) year += tenPow;
        
        printf("%d\\n", year);
    }

    return 0;
}

662B - Покраска графа

Идея задачи — gen

Решим задачу отдельно для перекраски всего в красный и перекраски всего в синий, и выберем лучший из этих двух вариантов. Далее рассмотрим задачу для перекраски всех ребер в красный.

Понятно, что бессмысленно выбирать одну и ту же вершину дважды, так как во второй раз мы просто поменяем цвета назад, поэтому наша задача — разбить вершины на два множества S и T, где S — это вершины, которые мы выберем для перекраски, а T — вершины, которые мы не будем трогать (все оставшиеся). Пусть вершины u и v соеденены красным ребром, тогда, чтобы цвет ребра остался красным, обе вершины u и v должны принадлежать одному множеству (обе S или обе T). Если же вершины u' и v' соеденены синим ребром, то они должны принадлежать разным множествам (мы хотим поменять цвет этого ребра ровно один раз, значит одна из вершин принадлежит S, а вторая — T).

Теперь наша задача — это 0-1 покраска графа, которую можно решить, к примеру, DFS-ом или BFS-ом. Так как граф может быть несвязный, то необходимо обрабатывать компоненты по одной. Если для какой-то компоненты 0-1 покраски не существует, то получить все ребра красного цвета мы не сможем. Если же для каждой компоненты у нас нашлась 0-1 покраска, то в множество S нам следует добавить меньшую из 0-1 долей, так как мы хотим минимизировать размер множества S.

#include<bits/stdc++.h>

using namespace std;

const int MX = 100000;

int n, vis[MX];
vector<pair<int, char>> G[MX];
vector<int> part[3];

bool dfs(int v, int p, char c) {
    if (vis[v] != 0) {
        return vis[v] == p;
    }

    vis[v] = p;
    part[p].push_back(v);

    for (auto x : G[v]) {
        if (dfs(x.first, x.second == c ? p : p ^ 3, c) == false)
            return false;
    }

    return true;
}

vector<int> solve(char c) {
    memset(vis, 0, sizeof vis);

    vector<int> ans;
    for (int i = 0; i < n; i++)
        if (vis[i] == 0) {
            part[1].clear();
            part[2].clear();

            if (dfs(i, 1, c) == false) {
                for (int j = 0; j < n + 1; j++) ans.push_back(-1);

                return ans;
            }

            int f = 1;
            if (part[2].size() < part[1].size()) f = 2;

            ans.insert(ans.end(), part[f].begin(), part[f].end());
        }

    return ans;
}

int main() {
    int m;
    scanf("%d %d", &n, &m);
    for (int i = 0; i < m; i++) {
        int u, v;
        char c;
        scanf("%d %d %c", &u, &v, &c);
        u--;
        v--;

        G[u].emplace_back(v, c);
        G[v].emplace_back(u, c);
    }

    auto f = solve('R');
    auto g = solve('B');

    if (g.size() < f.size()) f = g;

    if (f.size() > n) {
        printf("-1\\n");

        return 0;
    }

    printf("%d\\n", (int)f.size());
    for (int x : f) printf("%d ", x + 1);
    printf("\\n");

    return 0;
}

662A - Азартный Ним

Идея задачи — GlebsHP

Первый игрок не может выиграть только если xor-сумма всех чисел равна 0. То есть задача состоит в том, чтобы посчитать количество способов разложить карточки так, чтобы xor-сумма верхних чисел равнялась нулю.

Пусть 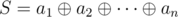, a 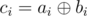. Пусть карточки с номерами j₁, j₂, ..., j_k лежат числами b вверх, а все остальные — числами a, тогда xor-сумма такой концигурации равна 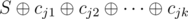, то есть 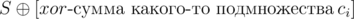. То есть мы хотим посчитать количество подмножеств c_i с xor-суммой S.

Заметим следующую особенность — если мы заменим в нашем множестве c₁ на , то ответ не изменится. Вместо {c₁, c₂} мы теперь можем взять , а вместо c₂ — 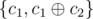. Поэтому мы можем выполнить следующие преобразования и ответ не изменится:

1. Выберем число c_f, в котором старший бит — еденица, если все элементы нули, то завершаемся
2. Заменим все остальные c_i, в которых старший бит тоже еденица на
3. Удалим число c_f из множество
4. Повторим действия 1-5 для оставшегося множества
5. Добавим c_f обратно в множество

После такого преобразования мы получим множество из k нулей и n - k чисел со свойством, что старший еденичный бит в этих счилах строго убывает. Как теперь проверить, можем ли получить xor-сумму S? Так как у нас осталось только одно число со старшим битом равным еденице, то старший бит зависит только от того, возьмем мы это число или нет. Так как мы знаем, каким этот бит должен получится в нашей xor-сумме, то мы можем однозначно определить, берем мы это число или нет. Аналогично продолжаем по всем следующим битам. Если в конце мы не получим подмножество с xor-суммой S, то эту xor-сумму получить невозможно (то есть второй игрок не может победить). Если же мы получили xor-сумму ровно S, то количество таких подмножеств будет 2^k, так как про n - k ненуллевых чисел мы уже однозначно определили, которые из них нам нужно взять, а из оставшихся k нулей мы можем выбрать произвольное подмножество и xor-сумму это не изменит. В данном случае вероятность победы второго игрока составляет 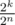, то есть ответ равен .

#include <bits/stdc++.h>

using namespace std;

const int size = 1000 * 1000 + 1;
const int ssize = 100;

int n;
long long a[size], b[size];
long long ort[ssize];
long long p[ssize];

int main() {
    long long cur = 0ll;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%lld%lld", &a[i], &b[i]);
        cur ^= a[i];
        a[i] ^= b[i];
    }
    a[n] = cur;

    int len = 0;
    for (int i = 0; i <= n; i++) {
        for (int j = 0; j < len; j++) {
            if (a[i] & p[j])
                a[i] ^= ort[j];
        }
        if (a[i]) {
            ort[len++] = a[i];
            p[len - 1] = ((a[i] ^ (a[i] - 1)) + 1) >> 1;
        }        
    }
    if (a[n]) {
        printf("1/1\\n");
    } else {
        printf("%lld/%lld\\n", (1ll << len) - 1, (1ll << len));
    }

    return 0;
}

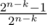662C - Двоичная табличка

Идея задачи — Alex_2oo8

Для начала рассмотрим медленное решение за O(2ⁿ · m). Давайте переберем все варианты по строчкам, каждую строчку мы либо будем инвертировать, либо не будем. Всю эту информацию можно сжать в битмаску — число от 0 до (2ⁿ - 1), где i-тый бит равен 1, если мы будем инвертировать i-тую строчку и 0, если не будем. Каждую из m колонок мы тоже можем сжать в битмаску над n битами (биты соответствуют значению в данной колонке на каждой из n строчек), обозначим битмаску для i-той колонки как col_i. Пусть маска строчек, которые мы будет инвертировать — это mask, тогда после того, как мы инвертируем все соответствующие строчки, в i-той колонке битмаска изменится на 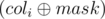. Пусть 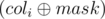содержит 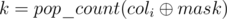еденичек, тогда мы можем получить в этой колонке либо (n - k) еденичек (если инвертируем i-тую колонку), либо k (если не будем инвертировать). Тогда для зафиксированной маски строчек mask минимальное количество еденичек, которое может остаться в табличке, равно .

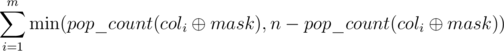Теперь мы хотим научиться считать последнюю сумму быстрее, чем за O(m). Заметим, что нас не интересует само значение маски 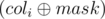, а только количество еденичек в ней (от 0 до n). Поэтому мы можем сгруппировать все колнки по значению 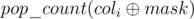, пусть dp[k][mask] — это количество таких i, что 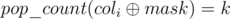, тогда мы можем посчитать сумму для фиксированной маски mask за O(n) — .

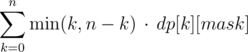Осталось только научиться быстро считать значения dp[k][mask]. Эти значение можно считать при помощи динамического программирования. dp[0][mask] можно легко посчитать за O(m) для всех mask — просто пробегаемся по всем колонкам и увеличиваем соответствующее значение dp[0][col_i] на 1. Для k > 0, col_i и mask отличаются ровно в k битах, переберем один из этих битов (бит, в котором будет отличие) и обозначим его за p. Тогда col_i и 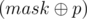отличаются ровно в (k - 1) битах. Казалось бы, количество таких колонок равно 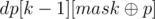, но нет, так как мы лишними учли все колонки, в которых col_i и 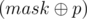отличаются в бите p (то есть бит p совпадает у mask и col_i). Снова, последнее количество почти равно dp[k - 2][mask], за исключением тех колонок, которые отличаються в бите p от mask. Пусть 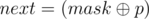, продолжая (что-то вроде принципа включений/исключений) мы получим, что количество, которое нас интересует равно dp[k - 1][next] - dp[k - 2][mask] + dp[k - 3][next] - dp[k - 4][mask] + dp[k - 5][next] - .... Что мы получим просуммировав такие значения по всем битам p? Мы получим dp[k][mask] · k, так как каждую колонку мы посчитаем ровно k раз (в каждом из битов, где есть отличие).

Таким образом, мы научились считать все значения dp[k][mask] за O(2ⁿ · n³) следующим образом:

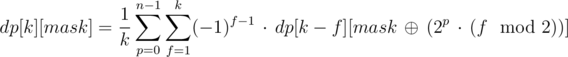
Это все еще слишком медленно, но пересчет динамики можно ускорить до O(2ⁿ · n²), к примеру, следующим образом:

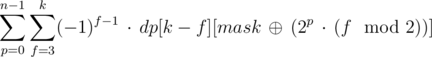
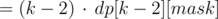
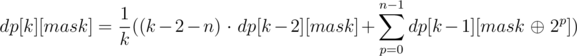
BONUS А вы можете решить эту задачу еще быстрее?

#include<bits/stdc++.h>

using namespace std;

char s[100000];
int col[100000], dp[21][1 << 20];

int main() {
    int n, m;
    scanf("%d %d", &n, &m);
    for (int i = 0; i < n; i++) {
        scanf(" %s", s);

        for (int j = 0; j < m; j++) col[j] |= (s[j] - '0') << i;
    }

    for (int i = 0; i < m; i++) dp[0][col[i]]++;

    for (int k = 1; k <= n; k++)
        for (int mask = 0; mask < (1 << n); mask++) {
            int sum = k > 1 ? (k - 2 - n) * dp[k - 2][mask] : 0;
            for (int p = 0; p < n; p++) sum += dp[k - 1][mask ^ (1 << p)];

            dp[k][mask] = sum / k;
        }

    int ans = n * m;
    for (int mask = 0; mask < (1 << n); mask++) {
        int cnt = 0;
        for (int k = 0; k <= n; k++) cnt += min(k, n - k) * dp[k][mask];

        ans = min(ans, cnt);
    }

    printf("%d\\n", ans);

    return 0;
}

662E - Взламывать или не взламывать

Идея задачи — Alex_2oo8

Первое наблюдение — так как взламывать можем только мы, то суммарный балл любого другого участника не может превышать 9000 (3 задачи по 3000 баллов), поэтому, если мы можем взломать как минимум 90 решений, то мы гарантированно можем занять первое место (только от взломов мы уже получаем 9000 баллов).

Теперь давайте решать задачу, зная, что количество потенциальных взломов не превосходит 90. Для начала — переберем конечную разбалловку (все 6³ вариантов). Теперь для каждой из задач мы можем однозначно определить, сколько взломов по ней мы сделаем (максимальное количество, после которого стоимость задачи будет такой, какую мы сейчас зафиксировали). Зная и конечную разбалловку, и количество наших взломов, мы можем посчитать свой суммарный балл. Теперь у нас есть участники, у которых мы ничего не можем взломать, на них мы уже никак повлиять не можем, поэтому можем уже посчитать, сколько из них нас обгоняют. Осталось не более 90 участников, у которых мы можем что-то взломать. Нас интересуют только те из них, кто на данный момент (пока мы у них ничего не взломали) нас обгоняют. Мы хотим как можно больше из них "скинуть" вниз. Эту задачу можно решать при помощи динамического программирования:

dp[p][i][j][k] — максимальное количество учасников среди первых p, которых мы можем "скинуть" вниз, взломав суммарно i раз по первой задаче, j по второй и k по третьей.

Переходы — перебираем множество задач, которые мы взломаем у следующего участника, и, если после этих взломов мы действительно "скинем" его вниз, то обновляем соответствующее значение ДП. К примеру, если достаточно взломать первую и третью задачи, то:

dp[p + 1][i + 1][j][k + 1] = max(dp[p + 1][i + 1][j][k + 1], dp[p][i][j][k] + 1)

BONUS А вы можете решить эту задачу, если за каждый успешный взлом дают 10 баллов, а не 100?

#include<bits/stdc++.h>

#define time ololo

using namespace std;

int time[5000][3], n, solved[3], canHack[3], score[3], willHack[3], bestPlace, dp[2][90][90][90], ci, li;

int submissionScore(int sc, int tm) {
    if (tm == 0) return 0;

    return sc * (250 - abs(tm)) / 250;
}

int calcScore(int p) {
    int sum = 0;
    for (int i = 0; i < 3; i++) sum += submissionScore(score[i], time[p][i]);

    return sum;
}

int countHacks(int p) {
    int cnt = 0;
    for (int i = 0; i < 3; i++) cnt += time[p][i] < 0;

    return cnt;
}

int solve() {
    memset(dp, 0, sizeof dp);

    int myScore = 0;
    for (int i = 0; i < 3; i++) myScore += 100 * willHack[i] + submissionScore(score[i], time[0][i]);

    ci = 0;
    li = 1;
    for (int p = 1; p < n; p++)
        if (countHacks(p) > 0 && calcScore(p) > myScore) {
            ci ^= 1;
            li ^= 1;

            for (int i = 0; i <= willHack[0]; i++)
                for (int j = 0; j <= willHack[1]; j++)
                    for (int k = 0; k <= willHack[2]; k++)
                        dp[ci][i][j][k] = dp[li][i][j][k];

            for (int ii = 0; ii < 2; ii++)
                for (int jj = 0; jj < 2; jj++)
                    for (int kk = 0; kk < 2; kk++) {
                        if (ii == 1 && time[p][0] >= 0) continue;
                        if (jj == 1 && time[p][1] >= 0) continue;
                        if (kk == 1 && time[p][2] >= 0) continue;

                        int s = submissionScore(score[0], time[p][0]) * (ii ^ 1)
                              + submissionScore(score[1], time[p][1]) * (jj ^ 1)
                              + submissionScore(score[2], time[p][2]) * (kk ^ 1);

                        if (s > myScore) continue;

                        for (int i = ii; i <= willHack[0]; i++)
                            for (int j = jj; j <= willHack[1]; j++)
                                for (int k = kk; k <= willHack[2]; k++)
                                    dp[ci][i][j][k] = max(dp[ci][i][j][k], dp[li][i - ii][j - jj][k - kk] + 1);
                    }
        }

    int res = 1 - dp[ci][willHack[0]][willHack[1]][willHack[2]];
    for (int p = 1; p < n; p++) if (calcScore(p) > myScore) res++;

    return res;
}

void brute(int p) {
    if (p == 3) {
        int res = solve();

        bestPlace = min(bestPlace, res);

        return;
    }

    for (int i = 0; i < 6; i++) {
        int mn = i == 5 ? 0 : (n >> (i + 1)) + 1;
        int mx = (n >> i);

        if (solved[p] >= mn && solved[p] - canHack[p] <= mx) {
            score[p] = 500 * (i + 1);
            willHack[p] = min(canHack[p], solved[p] - mn);

            brute(p + 1);
        }
    }
}

int main() {
    memset(solved, 0, sizeof solved);
    memset(canHack, 0, sizeof canHack);
    
    scanf("%d", &n);
    for (int i = 0; i < n; i++)
        for (int j = 0; j < 3; j++) {
            scanf("%d", &time[i][j]);

            solved[j] += time[i][j] != 0;
            canHack[j] += time[i][j] < 0;
        }

    if (canHack[0] + canHack[1] + canHack[2] > 89) {
        printf("1\\n");

        return 0;
    }

    bestPlace = n;
    brute(0);

    printf("%d\\n", bestPlace);

    return 0;
}