665A - Автобусы между городами
Задачу предложил Сергей Эрлих unprost.
Рассмотрим интервал времени, когда Симион будет находиться на трассе строго между городами (x1, y1), (x1 = 60h + m, y1 = x1 + ta). Переберём встречный автобус. Пусть (x2, y2) — это интервал времени, когда встречный автобус будет находиться строго между городами. Если пересечение этих интервалов (x = max(x1, x2), y = min(y1, y2)) не пусто, то Симион посчитает этот автобус.
Сложность: O(1).
665B - Покупки
Задачу предложил Ayush Anand JeanValjean01.
В этой задаче нужно было сделать ровно то, что написано в условии. Никаких хитростей и подвохов.
Сложность: O(nmk).
665C - Простые строки
Задачу предложил Zi Song Yeoh zscoder.
Для решения этой задачи есть два подхода: жадность и динамическое программирование.
Первый подход: Рассмотрим некоторый отрезок из подряд идущих одинаковых букв. Пусть длина отрезка k. Очевидно мы должны изменить хотя бы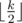 
букв в ней, чтобы не было одинаковых букв подряд. С другой стороны мы можем изменить второй, четвёртый и т.д. символы на букву, которая не равна букве слева и справа от нашего отрезка.
Второй подход: Пусть zka — наименьшее количество изменений, чтобы на префиксе длины k не было двух подряд идущих одинаковых букв и при этом символ s'k был равен букве a. Переберём букву, которую поставим на k + 1-й позиции и если она не равна a сделаем переход. Цена перехода равна 0, если мы поставили ту же букву, что стояла в исходной строке s на k + 1-й позиции. В противном случае цена равна 1.
Сложность: O(n).
665D - Красивое подмножество
Задачу предложил Zi Song Yeoh zscoder.
Рассмотрим подмножество A, являющееся ответом на задачу. Пусть a, b, c — три произвольных элемента из A и пусть не более чем один из них равен 1. По принципу Дирихле среди этих трёх чисел обязательно найдется пара чисел с одинаковой чётностью. Поскольку в этой паре только одно может быть равно 1, то их сумма чётна и больше 2. Значит подмножество A не является простым. Таким образом, A состоит либо из двух чисел больших единицы (с простой суммой), либо из некоторого количества единиц и возможно одной не единицы (если она равна простому минус один). Первый случай легко обработать за O(n2). Второй случай легко обрабатывается за линейное время. Среди двух ответов, конечно, нужно просто выбрать лучший.
Проверять на простоту числа порядка 2·106 за O(1) можно с помощью обычного или линейного решета Эратосфена.
Сложность: O(n2 + X), где X — максимальное среди заданных чисел.
665E - Красивые подмассивы
Задачу предложил Zi Song Yeoh zscoder.
Знак 
в разборе обозначает бинарную операцию побитового исключающего или.
Пусть si — xor первых i чисел на префиксе. Тогда полуинтервал (i, j] красивый если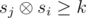 
. Будем перебирать j от 1 до n. Будем рассматривать значения sj как битовые строки. На каждой итерации к ответу нам нужно прибавить величину zj — количество чисел si (i < j) таких, что 
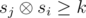. Для этого воспользуемся структурой данных бор. Будем хранить в боре все si для i < j. Кроме самой структуры бора будем в каждой вершине хранить количество листьев в поддереве этой вершины (это легко делать при добавлении новой строки). Для вычисления значения zj будем спускаться по бору, начиная из корня. Будем накапливать число cur равное префиксу ксора числа sj с путём по которому мы спустились по бору. Пусть текущий бит в sj равен b, а i — это глубина вершины в боре в которой мы находимся. Если число cur + 2i ≥ k, то мы сразу можем прибавить к zj количество листьев вершины 
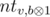, поскольку все эти листья соответствуют si-м гарантированно дающим 
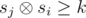. После этого мы должны спуститься в поддерево b. Если же cur + 2i < k, то мы должны просто спуститься в поддерево 
, пересчитав значение cur = cur + 2i.
Сложность по времени и памяти: O(nlogX), где X — наибольший из ксоров на префиксах.
665F - Четыре делителя
Разбор этой задачи является небольшой модификацией материалов лекции, прочитанной Михаилом Тихомировым Endagorion осенью 2015-го года в МФТИ. Большое спасибо Endagorion-у за предоставленные материалы.
Легко видеть, что только числа вида p·q и p3 (для различных простых p, q) имеют ровно четыре положительных делителя.
Посчитать количество чисел вида p3 можно просто за время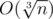 
, где n — это число из условия задачи.
Пусть теперь p < q и π(k) — это количество простых от 1 до k. Переберём значение p. Легко видеть, что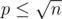 
. Таким образом, для фиксированного p мы должны увеличить ответ на значение 
.
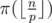Таким образом задача свелась к подсчёту значений 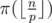— количество простых, не превосходящих величины 
для всех p.
Введём обозначение pj — j-е простое число. Пусть dpn, j — это количество k таких, что 1 ≤ k ≤ n и все простые делители k не меньше pj (заметим, что число 1 будет учтено во всех dpn, j, поскольку оно не имеет простых делителей). dpn, j удовлетворяет реккурентному соотношению:
dpn, 1 = n (поскольку $p_1$=2).
dpn, j = dpn, j + 1 + dp⌊ n / pj⌋, j, следовательно dpn, j + 1 = dpn, j - dp⌊ n / pj⌋, j.
Пусть pk — это наименьшее простое большее 
. Тогда π(n) = dpn, k + k - 1 (по определению первое слагаемое учитывает все простые не меньшие k).
Если вычислять реккурентность dpn, k напрямую, то все достижимые состояния будут иметь вид dp⌊ n / i⌋, j. Также можно заметить, что если pj и pk оба больше , то dpn, j + j = dpn, k + k. Поэтому, для всех ⌊ n / i⌋ нам достаточно хранить только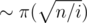 
значений dp⌊ n / i⌋, j.
Вместо прямого подсчёта всех состояний динамики, будем осуществлять двухшаноговый процесс:
Выберем K.
Запустим рекурсивное вычисление dpn, k. Если при этом в какой-то момент мы захотим посчитать значение для состояние n < K, запомним запрос ``посчитать количество чисел не больше n с простыми делителями не меньше k''.
Посчитаем ответы на все запросы в off-line: вычислим решето для чисел до K, отсортируем все числа по наименьшему простому делителю. Теперь мы можем ответить на все запросы, используя структуру данных на прибавление в точке и взятие суммы на отрезке (например, дерево Фенвика). Запомним все ответы глобально.
Снова запустим рекурсивное вычисление dpn, j. Но в этот раз если мы захотим посчитать значение для состояния n < K, мы можем использовать уже вычисленное значение.
Эффективность этой идеи сильно зависит от величины Q — количество запросов, которые нам придётся обработать.
Утверждение.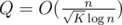 
.
Доказательство:
Каждое состояние для предпосчёта получено из dp⌊ n / pj⌋, j переходом из большего состояния. Из этого следует, что величина Q не превосходит общего количества состояний для n > K.
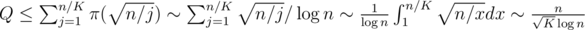
Предпосчёт ответов для Q запросов может быть выполнен за время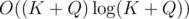 
и это наиболее ёмкая часть вычислений. Выбирая оптимальным образом значение 
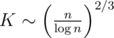, мы получаем сложность всего решения 
.
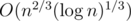Сложность: .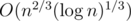
Автокомментарий: текст был обновлен пользователем Edvard (предыдущая версия, новая версия, сравнить).
Auto comment: topic has been updated by Edvard (previous revision, new revision, compare).
This problem is also an easier version of This Problem !
That's why you were able to solve it?
Yeah!
Cool. :)
Endagorion told me that there are something very similar at Project Euler. Also the problem to count semiprimes was last year at MIPT camp (the editorial from there). Anyway I think it's very good problem for Educational Round.
Funny:
A bit harder maybe, but all the same.
Can you explain your solution or provide some link to the theory behind it? It looks much simpler than author's.
Let S(v,m) be the count of integers in the range 2..v that remain after sieving with all primes smaller or equal than m. That is S(v,m) is the count of integers up to v that are either prime or the product of primes larger than m.
S(v, p) is equal to S(v, p-1) if p is not prime or v is smaller than p2. Otherwise (p prime, p2<=v) S(v,p) can be computed from S(v,p-1) by finding the count of integers that are removed while sieving with p. An integer is removed in this step if it is the product of p with another integer that has no divisor smaller than p. This can be expressed as
S(v,p)= S(v,p−1)− ( S(v/p, p−1)− S(p−1,p−1) ).
During computation of S(N,p) it is sufficient to compute S(v,p) for all positive integers v that are representable as floor(N/k) for some integer k and all p ≤ v1/2.
NOTE: Pi(N) = S(N,N). When you call S(N,N) it will need to compute S(N/k,N/k) in its lower substate. Hence you can have all required values of Pi(N/k).
In my code DSUM(N,P) do the job of calculating S(N,P).
I used two arrays H[] and L[] for storing the values of S(N/k,p) in H[k] for k<=N1/2 and for k>=N1/2 I stored the values of S(N/k,p) in L[N/k].
For computation I started with p=2 and changed the values of all the state which is going to be affected by this particular prime. Continue doing this for all prime till N1/2 and at the end for k<=N1/2, H[k] will contain the values of Pi(N/k) and L[k] will contain the values of Pi(k).
PS: My complexity is O(N3/4).
Idea: This Post!
Can I get your code please ???
Can you explain why the time complexity of your solution is O(N3 / 4)
(I find it difficult to calculate it)
Let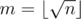
.
Notice that v could only be i or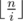
, where 1 ≤ i ≤ m, and for each S(v, v) we would enumerate 
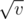values to calculate it. So the time complexity of the above algorithm is
The former part is always smaller than the latter, so we could only analysis the complexity of the latter part, which would be same order as
and it's $O(n^{3/4})$ .
By the way, if you preprocess the π(m) for m ≤ n2 / 3, you could find that the integral becomes
and it's $O(n^{2/3})$ . :)
I got AC there with the simple modification of the solution described in editorial:
В E есть еще другое решение.
Посчитаем количество подмассивов, xor которых строго больше k на 31м бите, затем на 30м бите (на 31м равно 31му биту числа k), затем на 29м (30й и 31й бит должны быть равны битам k) и т.д. Будем считать ответ для каждого бита, проходя слава-направо, и поддерживая количество xor'a равных x на префиксе. Решая задачу для 31..6 будем поддерживать количество xor'ов в обычном массиве
int cnt[1<<26], а для оставшихся 5..0 битов решим задачу с помощью хеш-мепа.Итого 1.4 сек на MSC++. 17408761
Мне кажется, что в E неудачно подобраны ограничения.
Если отказываться от C-style массивов и использовать
std::vector, то программа не влезает из-за оверхеда по памяти. Если переходы в боре делать с помощьюstd::map, то не проходит ещё и по времени.Is it possible to find these materials?
I think he means to refer to this http://www.ams.org/mcom/1996-65-213/S0025-5718-96-00674-6/S0025-5718-96-00674-6.pdf
In problem F, how the recurrence dp(n, j) = dp(n, j + 1) + dp(⌊ n / pj⌋, j) is being derived?
Here's what i think:
dp(n,j) counts all positive integers k with the properties:
Now we can split this set into 2 disjoint subsets:
k2 = pjar1a1r2a2... rvav = pj * k3,
where pj is the j-th prime number and r1, r2, ..., rv are all primes bigger than or equal to pj.
k3 is a number obviously in the range [1...⌊ n / pj⌋] with every factor in its PPF (Prime Power Factorization) being at least pj.There are dp(⌊ n / pj⌋,j) such numbers,so the recursion is correct.
в задача F для фиксированного p мы должны посчитать сколько простых чисел есть от 1 до n, которые большие чем p. т.к. мы берем что p<q.
Разве отсюда не получается что для фиксированного p мы должны взять pi(n/p)-pi(p)? Или я что-то неправильно понимаю
In problem D, "Let's define a subset of the array a as a tuple that can be obtained from a by removing some (possibly all) elements of it ". Is there exists any case where (possibly all) all elements will be removed,i can`t fix it..
No.
What is the best approach for B if the constraints were higher (10^5 instead of 100 ) ?
I have only one idea to optimise it to O(n*k*log(m)) using segment tree.
using penwick tree , we can solve O(n*m*log(k+n*m))
first we set the value Position[i] = position
a1 , a2 ,a3 ,.... an
Position[a1]= n*m+1, Position[a2]= n*m+2,... Position[ak] = n*m+k
and make variable pos = n*m;
and initialize penwick tree using Position[i] .
if we find item X, then add penwick_query(Position[x]) to return value.
and decrease_penwick(Position[x],-1) , Position[x]= pos--, penwick_increase(Position[x],1);
above action's time complexity is O(log(n*m+k) ).
do you mean fenwick tree?
also you can write an O(n*m*log(k)) solution with ordered set.
http://codeforces.net/contest/665/submission/19748159
In problem F, can someone explain the two-step process of evaluating the DP States better?
Can someone explain me the condition cur+2^i >=k in problem E?
A question regarding problem E. When I was solving the problem, instead of writing
int b = (x >> i) & 1;, I wroteint b = x & (1 << i). This change gave me AC (iwas in the same bounds as in the c++ solution).What's the difference?
Good day to you :)
It returns different value:
int b = (x >> i) & 1;Returns 1, if ith bit is 1int b = x & (1 << i);Returns 2^i, if ith bit is 1Hard to say, what happened next (for futher investigation, more code would be needed)
Hope it helped a bit ~ Good Luck :)
can anyone plz explain D in detail !
unable to grab it!
thnxxxx
1.If there's multiple ones in original set, we should choose them, because 1+1=2, 2 is a prime number.
2.Now consider what are the extra elements we should insert into the answer. I donate the answer is {1,1,....,1,A,B,C,....}, look at the {1,A,B}, there are three elements, each of them must be odd or even, so there must be two element have the same parity, so add them together will get a even number larger than 2, that is definitely not a prime number.
3.So you see, if we exclude all the ones in the answer, the answer size must less or equal to 2.
ans(Problem E) == (n * (n + 1) / 2) — ans(http://www.spoj.com/problems/SUBXOR/)
Hey guys, I use the DFS to solve problem D. I'm confused why my code passed test 11 only used 78ms where n equals to 1000, but get a TLE at test 12? here's my solution:code
Thanks
For E: Can someone please explain why we have to flip the bit b in function get()?
Thank you.
Так как это Educational round, то, возможно, для задачи 665A - Автобусы между городами будет не лишним упомянуть про альтернативное аналитическое решение без циклов. Нам нужно найти количество встречных автобусов, которые вышли из B до прибытия нашего автобуса в B. И найти количество встречных автобусов, которые прибыли в A до выхода нашего автобуса из A. Разница между этими числами и будет ответ. Пример: 17490212
Can someone explain what is RSQ structure? It is mensioned in problem F. Had no idea what it is. Thanks.
Could somebody explain me in problem E, why do we have to go down to the subtree (b xor 1) when (cur + 2^i) < k ?
In problem E , L can equal to R . So I think we should check each elements of the array if it >= k
mạnh
Now we can simply solve the problem F with min_25 sieve in $$$O(\frac{n^{\frac{3}{4}}}{\log n} + \sqrt n)$$$ !!
I sincerely agree with you. :)
And notice that you need to calculate $$$\pi(\lfloor\frac n x\rfloor)$$$, choose Meissel-Lehmer and combine with min-25 can you reach a more efficient solution.