Добрый день, Codeforces!
Меня интересует, умеет ли кто-нибудь считать такую сумму 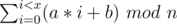 . Или такую сумму (они друг через друга выражаются)
. Или такую сумму (они друг через друга выражаются) 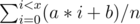 (деление целочисленное).
(деление целочисленное).
Буду очень признателен любым методам подсчета быстрее чем линия (или около-линия).
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
Добрый день, Codeforces!
Меня интересует, умеет ли кто-нибудь считать такую сумму 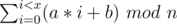 . Или такую сумму (они друг через друга выражаются)
. Или такую сумму (они друг через друга выражаются) 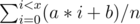 (деление целочисленное).
(деление целочисленное).
Буду очень признателен любым методам подсчета быстрее чем линия (или около-линия).
| Название |
|---|



Правильно понимаю, что модуль находится под суммой?
Да, правильно. Иначе тривиал =)
Дак модуль суммы равен сумме модулей же)
К.О.
Я не силен в математике, но разве по правилам не надо левую часть всю тоже по модулю взять? Тогда ведь все получается.
К.О. Так в условии этого mod нету, вот в чём прикол.
И вся сумма модулей берется по модулю, так что мы недалеко ушли.
ага)
Гер, скачай разбор отсюда. Задача aladin.
O(n), где n — размер модуля. Или это тоже имелось ввиду под линией?
Да это тоже слишком долго.
Вот в этой статье в разделе 3 эта сумма считается за .
.
Получается x*b+a*((x*(x-1)/2) (mod n). Но это слишком просто, чтобы писать пост; что я понял не так? :) upd: упс, надо было читать комментарии перед написанием своего.
как я понял, фича в том, что мы берем по модулю каждое слагаемое, но не берем сумму
На онсайте Opencup'а летом 2011 года была задача — посчитать количество целых точек в прямоугольном треугольнике. И решалась она за . Эта задача достаточно просто к ней сводится. Алгоритм решения примерно тот же самый, что и алгоритм из статьи из комментария выше.
. Эта задача достаточно просто к ней сводится. Алгоритм решения примерно тот же самый, что и алгоритм из статьи из комментария выше.
Коротко, и по русски ^_^
Научимся решать задачу для случая, когда a>=b.
Есть такое k, что a=k*b+c, где c<b.
Ответ, следовательно — [(k*b+c)/b]+[2(k*b+c)/b]+[3(k*b+c)/b]...+[n(k*b+c)/b].
Где [x] — то же самое, что и trunc(x).
На самом деле ответ состоит из двух частей — k+2k+3k+4k...+nk — это легко посчитать и [c/b]+[2c/b]+[3c/b]...+[nc/b] — это та же задача, только уже с новыми a,b,n.
Чтобы ее решить, просто как-бы мысленно повернем треугольник на 90 градусов и мы получим новые a,b,n для этого повернутого прямоугольника, хотя все равно понятно, что это будет одно и то же.
И эти a,b,n можно получить такими, чтобы выполнялось a>=b и опять решить задачу, которую мы научились решать.
И там еще надо будет немного повозиться с точками лежащими на гипотенузе.
На самом деле, все будет изменяться так же, как и в алгоритме Евклида. Так что мы получим решение за сложность, за которую работает Евклид, то есть за быстро.
Это примерные намеки на решение.
Мой код — решение задачи SPOJ GPINTRI.