Let's learn about Staircase Nim by solving move the coins problem that appeared in HackerRank April World Codesprint. Among the problems I have ever created, its one of my favorites. If you don't want to solve that problem but want to learn about staircase-nim, just read the first part of this blog.
Let's start with some backgrounds.
Staircase Nim
This problem is a variation of Staircase Nim problem, which is a not-very-well-known variation of classic Nim problem. If you don't know what Nim Game is, I suggest you first to learn about it.
In Staircase Nim, there is a staircase with n steps, indexed from 0 to n - 1. In each step, there are zero or more coins. See the figure below:
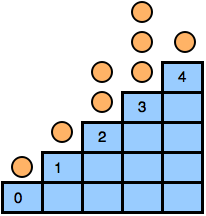
Two players play in turns. In his/her move a player can choose a step i > 0 and move one or more coins to step i - 1. The player who is unable to make a move lose the game. That means the game ends when all the coins are in step 0.
Now you have to decide who will win the game if both players play optimally.
Observation
We can divide the steps into two types, odd steps, and even steps. Now let's think what will happen if a player A move a coin from an even step to an odd step. Player B can move those coins to an odd position and the state of the game won't change.
But if A move a coin from an odd step to an even step, similar logic won't work. Because there can be situation where player B won't be able to move those coins to another odd step to restore the state.
From this we can agree that coins in even steps are useless, they don't affect game state. If I am in a winning position and you move a coin from an even step, I will move those coins again to another even step and will remain in a winning position.
Determine Winning Position
Now we agreed that only coins to odd steps count. If you take one or more coins from an odd step and move them to an even step, the coins become useless! Remember even steps are useless, So moving to even step is just like throwing them away. Now we can imagine coins in an odd-step as a pile of stones in a standard Nim game.
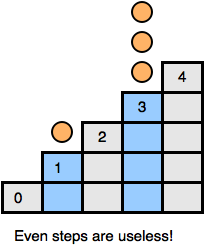
Now its easy, just find the xorsum of all odd steps and we are done!
Move the Coins
In the HackerRank problem, there is a tree and each node can contain zero or more coins.
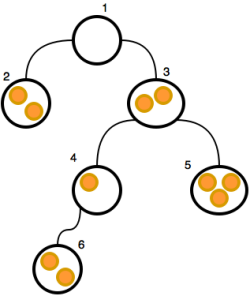
In each move, a player can move one or more coin from a node (which is not the root) to its parent node. If a player can't make a move, he/she loses the game.
This is same as Staircase nim but on a tree. You just need to calculate the distance between each node and the root. Now find the xorsum of all odd distance nodes. This can be done using a dfs, complexity O(V + E).
How to answer Alice's Questions?
Now, let's discuss updating the xorsum for each question. Suppose d1 is the distance between 1 and u. For node u, you must remove the edge between u and p(u) and add an edge between u and v. Suppose d2 is the new distance between u and 1; if d1%2 = d2%2, it won't change the xorsum because odd distance nodes still have odd distances (the same is true for even distance nodes).
If d1%2! = d2%2, all the odd distance nodes in subtree u will become even distance nodes, and all the even distance nodes in subtree u will become odd distance nodes. If you save the xorsum of odd and even distance nodes separately, you can easily update it for each question.
A question will be invalid if u and v belong to the same subtree. You can then easily find that using the finishing time in depth-first-search. Some did it by finding LCA but that's too much.
The complexity of answering each question is O(1).
That's all! I will be grateful if you point out the mistakes.
A Game Theory Contest
There will be a multi-day Game Theory Contest in HackerRank on 13th May, targeted mainly to the one who just started learning game theory but last two days will contain some harder problems.
The contest is prepared by allllekssssa, forthright48 and me (with the help of wanbo, as always). Hope to see you in the contest!











Nice, thanks!
Thanks for reading :).
Good tutorial !
We disscussed this by chat, but I read it again and now it is even more clear :)
I would like to call, once more, to game contest. It will be at least 15 tasks (I said 'at least' because only I wish one task, but rest of team thinks that is not good for educational round :P ). For my opinion contest will be interesting and useful for all participants. During preparation process I learnt several new things and I believe everyone also can find something new and at least a little exciting.
There are t-shirs for top 10 winners:) Maybe I will make some fake profile and got my first HR t-shirt ( I am joking :P ).
Good work!
By the way, the test data in the contest was quite weak. I implemented the "INVALID" check in O(n) time using a simple loop and got full score.
Thanks for pointing out. The main focus was on the game part, thats why may be I missed that INVALID check part. But I believe if someone can solve the main part, that part is easy :).
Thanks for reading.
I know I am a bit late, but there is a typo in the observation, the second line should be " B can move those coins to an even position", instead of " odd position"
Hello! Sorry for necroposting! I know this comment might be longer than the rest,but please read it! Something is not clear to me about the equivalence of the staircase nim and the game on the tree. In the tree version of the game,i think of each level of the tree as being a "stair". But unlike the staircase nim game,the maximum number of coins you can move down from that "stair" is the maximum number of coins in a single vertex. I fail to see how this games are equivalent,since in one version you are restricted on the number of coins you can move down. If someone could point out the mistake in my train of thought,I would greatly appreciate it.
Each level of the tree is not the stair. Each vertex is a stair, and you can think of the whole tree as being multiple branching staircases that all lead to the same root node.
Hi again! Thanks for your response,I did not expect to get one so quickly! I understood the solution now,you were of great help!