Editorial was created by Errichto, but he said that he has enough contribution, so I'm posting it for you. ;)
1 673A - Bear and Game
(invented by GlebsHP — thanks!)
You are supposed to implement what is described in the statement. When you read numbers ti, check if two consecutive numbers differ by more than 15 (i.e. ti - ti - 1 > 15). If yes then you should print ti - 1 + 15. You can assume that t0 = 0 and then you don't have to care about some corner case at the beginning. Also, you can assume that tn + 1 = 91 or tn + 1 = 90 (both should work — do you see why?). If your program haven't found two consecutive numbers different by more than 15 then print 90. If you still have problems to solve this problem then check codes of other participants.
2 673B - Problems for Round
(invented by Errichto)
Some prefix of problems must belong to one division, and the remaining suffix must belong to the other division. Thus, we can say that we should choose the place (between two numbers) where we split problems. Each pair ai, bi (let's say that ai < bi) means that the splitting place must be between ai and bi. In other words, it must be on the right from ai and on the left from bi.
For each pair if ai > bi then we swap these two numbers. Now, the splitting place must be on the right from a1, a2, ..., am, so it must be on the right from A = max(a1, a2, ..., am). In linear time you can calculate A, and similarly calculate B = min(b1, ..., bm). Then, the answer is B - A. It may turn out that A > B though but we don't want to print a negative answer. So, we should print max(0, B - A).
3 673C - Bear and Colors
(invented by Errichto)
We are going to iterate over all intervals. Let's first fix the left end of the interval and denote it by i. Now, we iterate over the right end j. When we go from j to j + 1 then we get one extra ball with color cj + 1. In one global array cnt[n] we can keep the number of occurrences of each color (we can clear the array for each new i). We should increase by one cnt[cj + 1] and then check whether cj + 1 becomes a new dominant color. But how to do it?
Additionally, let's keep one variable best with the current dominant color. When we go to j + 1 then we should whether cnt[cj + 1] > cnt[best] or (cnt[cj + 1] = = cnt[best] and cj + 1 < best). The second condition checks which color has smaller index (in case of a tie). And we must increase answer[best] by one then because we know that best is dominant for the current interval. At the end, print values answer[1], answer[2], ..., answer[n].
4 673D - Bear and Two Paths
(invented by Errichto)
There is no solution if n = 4 or k ≤ n. But for n ≥ 5 and k ≥ n + 1 you can construct the following graph:
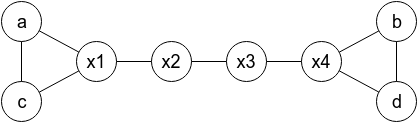
Here, cities (x1, x2, ..., xn - 4) denote other cities in any order you choose (cities different than a, b, c, d). You should print (a, c, x1, x2, ..., xn - 4, d, b) in the first line, and (c, a, x1, x2, ..., xn - 4, b, d) in the second line.
Two not very hard challenges for you. Are you able to prove that the answer doesn't exist for k = n? Can you solve the problem if the four given cities don't have to be distinct but it's guaranteed that a ≠ b and c ≠ d?
5 673E - Levels and Regions
(invented by Radewoosh)
When we repeat something and each time we have probability p to succeed then the expected number or tries is  , till we succeed. How to calculate the expected time for one region [low, high]? For each i in some moment we will try to beat this level and then there will be S = tlow + tlow + 1 + ... + ti tokens in the bag, including ti tokens allowing us to beat this new level. The probability to succeed is
, till we succeed. How to calculate the expected time for one region [low, high]? For each i in some moment we will try to beat this level and then there will be S = tlow + tlow + 1 + ... + ti tokens in the bag, including ti tokens allowing us to beat this new level. The probability to succeed is 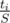 , so the expected time is
, so the expected time is 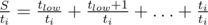 . So, in total we should sum up values
. So, in total we should sum up values 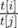 for i < j. Ok, we managed to understand the actual problem. You can now stop and try to find a slow solution in O(n2·k). Hint: use the dynamic programming.
for i < j. Ok, we managed to understand the actual problem. You can now stop and try to find a slow solution in O(n2·k). Hint: use the dynamic programming.
- Let dp[i][j] denote the optimal result for prefix of i levels, if we divide them into j regions.
- Let pre[i] denote the result for region containing levels 1, 2, ..., i (think how to calculate it easily with one loop).
- Let sum[i] denote the sum of tj for all 1 ≤ j ≤ i.
- Let rev[i] denote the sum of
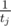 for all 1 ≤ j ≤ i.
for all 1 ≤ j ≤ i.
Now let's write formula for dp[i][j], as the minimum over l denoting the end of the previous region:
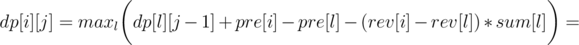
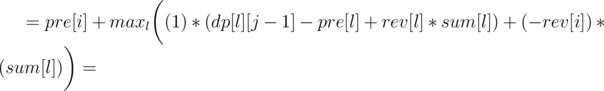
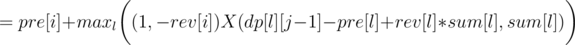
So we can use convex hull trick to calculate it in O(n·k). You should also get AC with a bit slower divide&conquer trick, if it's implemented carefully.
6 673F - Bearish Fanpages
(invented by Radewoosh)
Let's say that every company has one parent (a company it follows). Also, every copmany has some (maybe empty) set of children. It's crucial that sets of children are disjoint.
For each company let's keep (and always update) one value, equal to the sum of:
- the income from its own fanpage
- the income from its children's fanpages
It turns out that after each query only the above sum changes only for a few values. If a starts to follows b then you should care about a, b, par[a], par[b], par[par[a]]. And maybe par[par[b]] and par[par[par[a]]] if you want to be sure. You can stop reading now for a moment and analyze that indeed other companies will keep the same sum, described above.
Ok, but so far we don't count the income coming from parent's fanpage. But, for each company we can store all its children in one set. All children have the same "income from parent's fanpage" because they have the same parent. So, in set you can keep children sorted by the sum described above. Then, we should always puts the extreme elements from sets in one global set. In the global set you care about the total income, equal to the sum described above and this new "income from parent". Check codes for details. The complexity should be 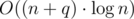 , with big constant factor.
, with big constant factor.
7 674E - Bear and Destroying Subtrees
(invented by Errichto)
Let dp[v][h] denote the probability that subtree v (if attacked now) would have height at most h. The first observation is that we don't care about big h because it's very unlikely that a path with e.g. 100 edges will survive. Let's later talk about choosing h and now let's say that it's enough to consider h up to 60.
When we should answer a query for subtree v then we should sum up h·(dp[v][h] - dp[v][h - 1]) to get the answer. The other query is harder.
Let's say that a new vertex is attached to vertex v. Then, among dp[v][0], dp[v][1], dp[v][2], ... only dp[v][0] changes (other values stay the same). Also, one value dp[par[v]][1] changes, and so does dp[par[par[v]]][2] and so on. You should iterate over MAX_H vertices (each time going to parent) and update the corresponding value. TODO — puts here come formula for updating value.
The complexity is O(q·MAX_H). You may think that MAX_H = 30 is enough because 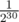 is small enough. Unfortunately, there exist malicious tests. Consider a tree with
is small enough. Unfortunately, there exist malicious tests. Consider a tree with 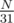 paths from root, each with length 31. Now, we talk about the probability of magnitude:
paths from root, each with length 31. Now, we talk about the probability of magnitude:
which is more than 10 - 6 for d = 30.
http://www.wolframalpha.com/input/?i=1+-+(1-(1%2F2)%5Ed)%5E(N%2Fd)+for+N+%3D+500000+and+d+%3D+30
8 674F - Bears and Juice
(invented by Radewoosh)
Let's start with O(q·p2) approach, with the dynamic programming. Let dp[days][beds] denote the maximum number of barrels to win if there are days days left and beds places to sleep left. Then:
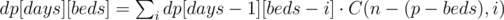
Here, i represents the number of bears who will go to sleep. If the same i bears drink from the same X barrels and this exact set of bears go to sleep then on the next day we only have X barrels to consider (wine is in one of them). And for X = dp[days - 1][beds - i] we will manage to find the wine then.
And how to compute the dp faster? Organizers have ugly solution with something similar to meet in the middle. We calculate dp for first q2 / 3 days and later we use multiply vectors by matrix, to get further answers faster. The complexity is equivalent to O(p·q) but only because roughly q = p3. We saw shortest codes though. How to do it guys?
You may wonder why there was 232 instead of 109 + 7. It was to fight with making the brute force faster. For 109 + 7 you could add sum + = dp[a][b]·dp[c][d] about 15 times (using unsigned long long's) and only then compute modulo. You would then get very fast solution.
9 674G - Choosing Ads
(invented by qwerty787788)
Let's first consider a solution processing query in O(n) time, but using O(1) extra memory. If p = 51%, it's a well known problem. We should store one element and some balance. When processing next element, if it's equal to our, we increase balance. If it's not equal, and balance is positive, we decrease it. If it is zero, we getting new element as stored, and setting balance to 1.
To generalize to case of elements, which are at least 100/k%, we will do next. Let's store k elements with balance for each. When getting a new element, if it's in set of our 5, we will add 1 to it's balance. If we have less, than 5 elements, just add new element with balance 1. Else, if there is element with balance 0, replace it by new element with balance one. Else, subtract 1 from each balance. The meaning of such balance becomes more mysterious, but it's not hard to check, that value is at least 100/k% of all elements, it's balance will be positive.
To generalize even more, we can join two of such balanced set. To do that, we sum balances of elements of all sets, than join sets to one, and then removing elements with smallest balance one, by one, untill there is k elements in set. To remove element, we should subtract it's balance from all other balances.
And now, we can merge this sets on segment, using segment tree. This solution will have complexity like n * log(n) * MERGE, where MERGE is time of merging two structures. Probably, when k is 5, k2 / 2 is fastest way. But the profit is we don't need complex structures to check which elements are really in top, so solution works much faster.










Why is there no solution if n = 4 in Div. 2 D?
Consider all possible graphs with 4 vertices. None of them satisfies the given conditions.
thanks.
If you got 4 vertices, for example A=1 B=4 C=2 D=3 , you will find out that from A to B you must pass the road C-D , however according to the problem statement, there should be no road between C and D.
Notice there should not be an edge between (a,b) and (c,d)! Then I think you can find it out by simple discussion. :D
I hadn't noticed that :'(
Question : for problem C, I got TLE by using this method. Can someone explain me why ?
http://codeforces.net/contest/673/submission/17783685
Thanks in advance.
I think it's just because of python :P
So, no hope for me to get AC ? :( Seriously, is it possible that some problems cannot be solved with all languages ?
I think the method you use is correct. (Same as mine and the one mentioned in editorial)
But I'm not sure if there is a better implementation in python to pass this problem.
Oh rip, i took MAX_H = 23 in the expected height problem...
In problem F it can easily be seen that R(i) is a polynomial of i with degree P. I wish modulo was prime, so we could interpolate the polynomial easily. Anyway, I had to look for patterns and it seems that polynomial is: R(i) = C(N, 0) + C(N, 1)*i + .. + C(N, P)*i^P.
What is the convex hull trick to speed up Div 2 E?
Blog
Which problems did each of the setters contribute?
We will put this info in the editorial.
I read your original comment before you erased it, but okay, thanks. =)
1) It wasn't correct (Mateusz told me that after a moment). Now you may wonder what was wrong.
2) It turns out I shouldn't give this info before the system testing. Let's pretend you haven't seen it.
EDIT — updated :)
Some source for improving on probability concepts?
I was unable to take out probability for a segment though I thought of trying dp with exactly same state(I didn't knew the convex hull trick though(Saw it somewhere but didn't knew much about it)).
Here is a solution to problem F. Associate to each barrel a n-tuple of integers (a1, a2, ..., an) where at most min(n - 1, p) of the ai are nonzero. On day r have bear k drink from a barrel if and only if ak for that barrel is equal to r.
Then no matter what barrel contains wine, it will make at most min(n - 1, p) bears die, and you can figure out the barrel uniquely from which bears and days died since all the n-tuples are distinct.
Therefore the maximum number of barrels is the number of such n-tuples which is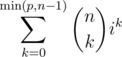 , if there are i days.
, if there are i days.
Alternatively, I noticed that the answer is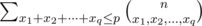 by a similar argument to above. The sum indeed simplifies to the above without too much work, but I did something a lot stupider. Instead, only compute the answer for the cases where xi > 0 for all i. After that, for large q note that most of the xi have to equal 0, so we can compute a lot of binomial coefficients to do this correctly.
by a similar argument to above. The sum indeed simplifies to the above without too much work, but I did something a lot stupider. Instead, only compute the answer for the cases where xi > 0 for all i. After that, for large q note that most of the xi have to equal 0, so we can compute a lot of binomial coefficients to do this correctly.
Mine is something like O(p3 + pq).
I think solution on "Choosing Ads" described shouldn't pass.
As I know, authors solution in following:
Let's first consider a solution processing query in O(n) time, but using O(1) extra memory. If p = 51%, it's a well known problem. We should store one element and some balance. When processing next element, if it's equal to our, we increase balance. If it's not equal, and balance is positive, we decrease it. If it is zero, we getting new element as stored, and setting balance to 1.
To generalize to case of elements, which are at least 100/k%, we will do next. Let's store k elements with balance for each. When getting a new element, if it's in set of our 5, we will add 1 to it's balance. If we have less, than 5 elements, just add new element with balance 1. Else, if there is element with balance 0, replace it by new element with balance one. Else, subtract 1 from each balance. The meaning of such balance becomes more mysterious, but it's not hard to check, that value is at least 100/k% of all elements, it's balance will be positive.
To generalize even more, we can join two of such balanced set. To do that, we sum balances of elements of all sets, than join sets to one, and then removing elements with smallest balance one, by one, untill there is k elements in set. To remove element, we should subtract it's balance from all other balances.
And now, we can merge this sets on segment, using segment tree. This solution will have complexity like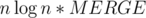 , where MERGE is time of merging two structures. Probably, when k is 5, k2 / 2 is fastest way. But the profit is we don't need complex structures to check which elements are really in top, so solution works much faster.
, where MERGE is time of merging two structures. Probably, when k is 5, k2 / 2 is fastest way. But the profit is we don't need complex structures to check which elements are really in top, so solution works much faster.
This is a great explanation of my solution :)
If somebody wants to know details or wants to know why does this work, I can answer all the questions.
Also I really want solution like "pick 50 random numbers on segment, check them, add some breaks" not to pass, but I'm not sure if I succeeded in generating good tests.
Why does my solution 17788912 in O(n^2*logn) fail with TL on the problem C? I suppose 5000*5000*log5000 should be fast enough for 2secs, no ?
Codeforces servers do 10^8 operations in one sec.Your algorithm does ~3*10^8
No,they can do 109 simple operations in ~300-500 ms or less but here it's just because STL is slow.BTW,if they would put n <= 1000 then O(n^3) would pass.
The fact is that localy it works for 20secs for max test. Is that really a problem of STL?
If it takes 20 secs in your machine maybe you shouldn't have submitted it.
I couldn't believe that n^2logn may be TL with n = 5000 so much that hadn't done max test before submitting.
Its happened first time with me this is my Div2 D soln which was hacked — > http://codeforces.net/contest/673/submission/17796235 after contest i submitted this code again — > http://codeforces.net/contest/673/submission/17798097
( which got accepted ! and the test case on which my code was hacked seems to give correct result ) Am i missing some thing or is it just my hard — luck ???
You submitted 2 solutions that passed pretests, and that correct one was your first, but your second was incorrect! When your most recent solution is hacked, it seems all previous submissions (that also pass pretests) also appear as hacked. That's unfortunate...
can i do anything about it ??
I don't think so, as the rules suggest only the last solution that passes pretests is considered. Yet I believe they should make it so that the submissions other than the hacked ones don't appear as hacked but something like Skipped instead to avoid misunderstandings.
My solution to G is different.
To answer a query of type 2, let's choose 500 random positions from the segment [l, r]. The probability that some number that needs to be printed is not present in the chosen set is negligibly low. Now, let's sort all chosen numbers by the number of times they were chosen (among 500 random positions) in descending order. For every number we can find how many times it is present in the segment [l, r] in with SQRT decomposition (all update queries of type 1 can be also done in
with SQRT decomposition (all update queries of type 1 can be also done in  ). If we met a number that's present in <=10% positions 11 times in a row, stop the procedure (as it's very unlikely that we'll meet a number with >=20% presence after this, the exact probability is of the order of 1e-10).
). If we met a number that's present in <=10% positions 11 times in a row, stop the procedure (as it's very unlikely that we'll meet a number with >=20% presence after this, the exact probability is of the order of 1e-10).
Overall complexity is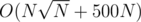 .
.
Could you please elaborate on "as it's very unlikely that we'll meet a number with >=20% presence after this"?
How can we calculate a probability of this?
Well, if a number A with percentage >=20% occurs exactly X times among 500 chosen numbers, then the probability of this is at least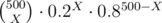 . This probability is >= 10 - 12 when 43 ≤ X ≤ 166 (if the percentage is greater than 20%, then both of these boundaries will only increase). So if we want the remaining 11 integers to be more frequent than A, then each of them has to occur at least 43 times among 500 chosen ones which is impossible because 12·43 > 500. As for the remaining cases when X < 43 or X > 166, the probability of this is < 10 - 12 and the probability that there will be 11 integers among the remaining ones which are more frequent than A is clearly less than 1, which means overall probability of all these scenarios is less than 10 - 12·500 < 10 - 10.
. This probability is >= 10 - 12 when 43 ≤ X ≤ 166 (if the percentage is greater than 20%, then both of these boundaries will only increase). So if we want the remaining 11 integers to be more frequent than A, then each of them has to occur at least 43 times among 500 chosen ones which is impossible because 12·43 > 500. As for the remaining cases when X < 43 or X > 166, the probability of this is < 10 - 12 and the probability that there will be 11 integers among the remaining ones which are more frequent than A is clearly less than 1, which means overall probability of all these scenarios is less than 10 - 12·500 < 10 - 10.
Fucking convex hull trick!!!
IMHO, it's a vulgar manners to give a DP problem, which could not be solved without it.
Throw out your emotions and note that CHT is just a standart well-known algorithm. Are you crying this way if you can't solve, for example, shortest path without Djkstra? (:
Comparing convex hull to Dijkstra is like comparing half-planes intersection to merge sort, as for me
Ehm, or like comparing banana with a helicopter. Just another bad comparison.
The convex hull trick is a popular and useful (and really easy!) concept that a competitor should know in order to succeed in contests. After all, that's one of the most powerful instruments to reduce magnitude of an optimizational DP complexity.
Helicopter is much better than banana because there you can't say that your gender is banana.
It became popular only 1-2 years ago, so many people who stopped competing before that time don't know it.
It was already very popular in 2012-2013 season, and it even appeared in WF 2011.
2012-2013 is the season when our team went to World Finals, and I still don't remember any CHT problem. Probably only high-level red teams were solving these problems then.
Some old problems on CHT:
Problem B here (May 2012).
Problem C of CF Round #189 (June 2013).
I'm sure that there was at least one problem on CHT in Petrozavodsk Winter camp 2013, but I can't prove it easily since the statements are not available in public.
The PEGWiki article gives sample problems from 2008 and 2010.
It was also used at CEOI 2009,problem Harbinger(CHT on tree).
Here you can submit it
... if you are IGM :)
Why do you think it's not easy? :( I wrote N^2*K solution and submitted it to see is there any bugs, then I added CHT and got accepted. You can look my submissions, there's only 10 minutes between them and just a few lines of code. If you know what is CHT and how to implement it, it becomes really easy.
Thanks! I'll take a look at your submissions, it should be very useful.
It's about comparing it to other tricks/algorithms, not about how strong someone is. Also, Zlobober's comment explains why one should learn CHT. So, maybe spend some time and learn it, instead of complaining and swearing.
Yes, I should spend some time to learn and deeply understand CHT.
But in this round, taking in attention the gap between B and C, it was excessive to require CHT or other optimization.
:) Yeah, you are right about shortest path.
But the C problem was nice enough and difficult enough (at least for 1500 in comparison with B for 1000) without requiring CHT skill.
P.S. Do you like problems, which main idea is based on some known, but not trivial algorithm?
Write a segment tree — and you can answer the questions.
Write a bitmask DP — and you can split anything.
Write a Z-function — and you can find the most common prefix.
I don't tell about DIV2A/B.
One could argue that whenever we solve problems, we do that by applying a series of previously learnt tricks. (Even a solution from first principles is based on tricks learnt in early childhood. What are "first principles" anyway? Nobody knows; otherwise they could write software to solve arbitrary algorithmic contests.)
But here's a conjecture: that whenever the difficulty of inventing a trick independently is much greater than giving up and learning it from the editorial, such a trick is likely to have a name.
I solved this problem without using convex hull trick, so maybe you could too.
I was trying it about 2 hours.. Could you decribe your solution?
You can use an divide and conquer approach to optimize your dp in a more simple way than with the CHT. Even n * log n * k is about 3*10^8, which easily fits in 3 seconds.
The key is that during the transition, e.g. during calculating a state, you don't need to loop through the entire previous dp[][] row, you can already know exactly where you need to look.
The concept is explained really well here: http://codeforces.net/blog/entry/8192 , and can be used in the identical way for this task. The explanation is in the bottom, for the task Ciel and Gondolas.
How long have you typically coded it?
I figured out the n^2*k in the end, and then convert it to convex hull form, and until now I haven't finished the code. How can div-1 coders code so fast?
(I am not the only one, in our division only ten or so can code it successfully)
I copied my CHT code from some past APIO problem and slightly modified it.
Really, it's not that much to type: the entire solution can fit in a screen. Most of the time is spent actually inventing the solution, and to do this quickly, you need to know many algorithms and techniques. For example, I already knew how to code the divide-and-conquer method to optimize the dynamics from O(n2) to , so I didn't have to engineer the code, just type it (and the code is short, so this doesn't take much time).
, so I didn't have to engineer the code, just type it (and the code is short, so this doesn't take much time).
Can someone explain how to recalculate the probabilities in "Bear and Destroying Subtrees"? I tried to understand people's code, but it is not very intuitive.
For Bear and Two Paths (Div 2. D), how to prove that for k<=n there is no answer?
n-1 roads are required to go from a to b. now since there is no road between a and b to go from c to d you cannot use all the previous n-1 roads. after little bit of thinking you can prove that you need at least two more roads.
There must be a hamiltonian path from a to b so n — 1 edges are needed for that. Now there must exist another path from c to d without using ( a — b ) ( c — d ) edge. Any path going from c to d involve going in & out of node a and b, so there must be at least two incident edge on both nodes. None of this edge may be the same due to the restriction mention earlier, so you need n — 1 edge from the original path + 2 new edge incidents to a and b respectivily. This implies that at least n + 1 edges are needed. Note that we are using the fact that none of a, b, c & d are the same.
Could you describe a DIV1-C solution based on Command and Conquer?
A little bit of feedback about editorial: please do not skip a non-obvious solution steps.
Dp can be formulated like this: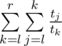 and can be calculated in O(1) using formulas from editorial. Now, we need to check sufficient condition for divide-and-conquer optimization : optimal i (where minimum is achieved in dp recalculation formula) is non-decreasing function of n for fixed k. It is true, because if i2 < i1, n2 > n1, then
and can be calculated in O(1) using formulas from editorial. Now, we need to check sufficient condition for divide-and-conquer optimization : optimal i (where minimum is achieved in dp recalculation formula) is non-decreasing function of n for fixed k. It is true, because if i2 < i1, n2 > n1, then 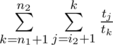 , second is
, second is 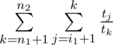 , which is smaller, because i2 < i1). So actually, i1 was not optimal for n1. So we see that divide-and-conquer optimization is applicable.
, which is smaller, because i2 < i1). So actually, i1 was not optimal for n1. So we see that divide-and-conquer optimization is applicable.
dp[k][n] = min(dp[k - 1][i] + cost(i + 1, n)), wheredp[k][n]is minimum expected time over all splittings first n levels in k areas.cost(l, r)isdp[k - 1][i_2] + cost(i_2 + 1, n_2) < dp[k - 1][i_1] + cost(i_1 + 1, n_2)leads todp[k - 1][i_2] + cost(i_2 + 1, n_1) < dp[k - 1][i_1] + cost(i_1 + 1, n_1), becausecost(i_2 + 1, n_2) - cost(i_2 + 1, n_1) > cost(i_1 + 1, n_2) - cost(i_1 + 1, n_1)(first isIf you don't know what divide-and-conquer optimization is, than there is the rough idea: if recalculation formula is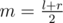 , that gives you range where optimal i has to be for
, that gives you range where optimal i has to be for 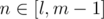 and
and 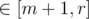 (for first segment it should be not more than for m, for second not less). Then you recurse and pick medians of this intervals and so on.
(for first segment it should be not more than for m, for second not less). Then you recurse and pick medians of this intervals and so on.
dp[k][n] = min(dp[k - 1][i] + cost(i + 1, n))for some cost(l, r) such that optimal i is non-decreasing function of n for fixed k. If you want to calculatedp[k][n]for l ≤ n ≤ r, then you can firstly calculatedp[k][m], whereI claim that it takes time in total for each k. It is because on each level of recursion tree (which has depth
time in total for each k. It is because on each level of recursion tree (which has depth  , because you always pick median of segment) only O(n) candidates for optimal i will be checked.
, because you always pick median of segment) only O(n) candidates for optimal i will be checked.
UPD. Fixed a typo. And one more.
Shouldn't it be l ≤ n ≤ r?
dp[k - 1][i_2] + cost(i_2 + 1, n_1) > dp[k - 1][i_2] + cost(i_1 + 1, n_1)— is it OK?and i2 < i1, n2 > n1?
LOL, you just occasionally spoiled your proficiency in computer games :)
In Div2E solution: why are we searching for the
lthat yields the maximum value instead of the minimum value?I recommend this awesome blog if you want to learn DP optimizations.
Again English got me!
I misread B many times.
Each problem used in division 1 should be harder than any problem used in division 2.
When I will learn? ;_;
For Div1 F,can someone explain the dp formula in detail? I can't understand why it's been added up.
Have you read the paragraph just after the formula?
Yes,but why to sum up not to find maximum?
We don't have to choose one i (the number of bears who will go to sleep). Consider the sample test (3 2 1). There is one day and bears can manage 7 barrels:
For example, if bears 2 and 3 will go to sleep then for sure wine is in barrel 4.
Now, regarding your question.
Analyze this test to see that we should add 1 + 3 + 3.
In Div1 E, why are we storing dp[v][h] as probability of height at most h and why not exactly equal to h? And why will adding new vertex to v affects dp[v][0], dp[par[v]][1]....only. Suppose we have 4-3-2-1-5(rooted at 1) and we add new vertex to 5, won't it affect dp[1][2], because now we will have more ways to make height of subtree rooted at 1 equal to 2? And what's the formula for doing the changes. I saw many codes but still understand how the formula came?
Indeed, there are more ways that the height will be exactly 2. And the probability for height exactly 2 is bigger than before. What we calculate though is the probability of height at most 2 and it doesn't change. The new edge can only change height from 1 to 2.
Regarding the formula. We are at vertex v. What is the probability that we will get height at most h? Let c1, c2, c3, ... denote children of v. We get height at most h if for each ci one of two holds true:
So, for each ci we have probability 1 / 2 + 1 / 2·dp[ci][h - 1].
Even if we store dp[v][h] which is height of subtree of v exactly equal to h, and suppose I add new vertex to v, then still only (dp[v][0],dp[v][1]),(dp[par[v]][1],dp[par[v]][2])... will change. The only difference will be I won't get such formula for calculating dp array. I will have to do much work for calculating dp array. Am I correct?
Yes, I think it's possible and slightly more complicated.
I am not able to open editorial's submission for problem E(Levels and Regions) or in fact any of the submissions. Getting the error "You are not allowed to view the requested page". Is this because parent contest is still in progress?
Lol, with 2^32 you can just do sum += dp[a][b]·dp[c][d] in uint32_t without any modulo anywhere. That's still not fast enough though.
What is your point? Yes, we should use addition and multiplication with uint32. The point is that there are no tricks now that would make the brute force faster. Because now both the intended and slower solution don't use modulo at all.
The goal was to easily distinguish the intended and slower solution.
Oh, it's to make the "non-optimized" good solution faster, this makes sense. I thought it was supposed to make the bad solution slower.
Sorry for a question, but I still could not understand the editorial solution about "Levels and Regions"
As I've got from Convex Hull description, it's about bringing solution to N linear functions and "drawing a hull".
But I don't see a linear functions from the formulas, because I suppose, that part "-rev[i] * sum[l]" could not be linear in a common case.
Also, suppose, that there is a mistype in the last formula ("1, — rev[i]" .. ")X(" .. "*sum[l],sum[l]"), I tried to a lot of transformations, but could understand, what was implied and how it can be transformed into linear function.
If it is not inconvenient to you, please, give some tips about it :)
P.S. Submission 17800506 (link from editorial) is not available.
Sorry for links, they should be changed soon. You can see the intended solution here for now.
Let's fix j. We have:
In the last formula we find $max$ over something of form a·x + b where only x depends on i. It doesn't bother us that there is also consti because we can add it at the end, after finding max (max is the hardest part). Ask me here or by PM if you still have doubts/questions. But I won't answer today, sorry (going to sleep).
Could anyone explain "Levels and Regions" without using mathematical formulas? I've been trying this for a long time but I can't grasp the idea behind those long formulas.
What is in those formulas except additions and multiplications? I don't know how to explain them without maths.
I usually think of DP solutions in terms of "we know X, therefore we know Y", where X and Y are something simple to understand. In this case X is a long formula with many individual parts and I'm not sure what those parts represent or how they're wired together. For example, I don't understand what rev[l] * sum[l] represents and I don't understand why we're calculating max rather than min.
I discovered a O(n^2 + k * n) solution, but I don't think this solution can be optimized to O(n * k).
Yes, it should be
mininstead ofmax.dp[i][j] = dp[l][j - 1] + S where S denotes the cost of interval [l + 1, i]. You can see in the editorial that S is the sum of t[a] / t[b] for l + 1 ≤ a < b ≤ i. Try to express this sum using arrays defined in the editorial: pre, sum and rev.
This was helpful. Thank you!
Finally got it! A lot of thanks for your huge help! :)
You can try to look at available submissions and see if you can understand any of them. For example, this one appears to use CHT.
Problem E is really cool. As i increases the (1, -rev[i]) decreases, Also, the slope of lines is increasing, thus directly adding lines as i increases will result in the 'convex hull' extending left, which coincides with how queries move. Though anti-intuitive, but wow, it is cool.