Hello all! :)
I stumbled upon this problem but I do not know how to solve it.
http://www.spoj.com/problems/ADDLCM/
The sum can be written as
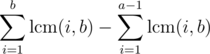
but this doesn't make the problem any easier. I can evaluate the first sum but its not easy to evaluate the second. Please give me some ideas to solve this.
Any help is appreciated. Thanks!











This will help blog
I already read it but I do not see how to simplify the second sum in terms of totient function.
We have to basically calculate:
Now , using the property
The summation changes to :
(See I have change the limits that is why an extra N on the left side as i=N is trivial) Now writing the summation in reverse order:
Adding the first and this equation you get:
which can be computed and we can output x.
Please read the problem I am trying to ask. I already know how to evaluate the sum you have mentioned (basically the first sum in OP), I am facing trouble evaluating the second sum, the limits of which do not end at b. Thanks!
Anyone? I am really stuck on this one for a long time. I feel this can be solved with Mobius inversion but given my inexperience with that, I am not sure how to proceed in that direction.
As before, any help is appreciated. Thanks!
Detailed Editorial : https://discuss.codechef.com/questions/4258/lcm-editorial
Hello MedoWith11Es! I have already seen that editorial (believe me, I have looked at a lot of stuff for this problem) but I think these two problems are very different or maybe I a overlooking something. Can you please show how these two problems relate to each other?
You can transform the sum a bit to a sum of expressions like this:
i.e. a sum of numbers relatively prime to z. As z ≤ 106, it can't have more than 7 prime divisors, and the sum can be calculated quite fast using the inclusion-exclusion principle.