DonMichaelCorleone's blog

How to calculate (a! / b!) % mod
By DonMichaelCorleone, history, 8 years ago, In English

How to calculate (a! / b!) % mod where n is 1<=n<=20000000, m is 1<=m<=n and mod is a positive integer ?

  • Vote: I like it
  • +7
  • Vote: I do not like it

»
8 years ago, # |
← Rev. 3   Vote: I like it +12 Vote: I do not like it

If you want to avoid multiplicative inverses, as the limits are <= 2e7, you can create a segment tree. If you divide a! by b!, you want to multiply the numbers b+1, b+2,....a. You can use a segment tree to do each query in O(logn), after building the segtree in O(n). You can also use a sparse table (similar to that explained in this [Topcoder tutorial](https://www.topcoder.com/community/data-science/data-science-tutorials/range-minimum-query-and-lowest-common-ancestor/#Sparse_Table_(ST)_algorithm)) to speed it up and solve each query in O(1), after preprocessing in O(n*logn). Note that this approach will work due to low limits (2e7).

UPD: The sparse table approach will also be O(logn) and not O(1). See FatalEagle's comment. :)

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    How to build segtree in O(n) time?

    UPD. Yes, O(4*N) = O(N). My mistake.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Segment tree is usually built in O(N) — it is a simple dfs.

      → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +24 Vote: I do not like it

    Can you describe the sparse table approach in more detail? The one in the tutorial seems to rely on the fact that counting the same element twice in the min function won't change the result.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Aah, right. My bad. The sparse table approach will also be logn, and not constant time, due to the reason you pointed out above. :)

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 5   Vote: I like it +30 Vote: I do not like it

      There is a way of building sparse table in so that you won't have to consider element twice.

      I'm not completely sure that this is called sparse table, but as far as Burunduk1 told me, it has something to do with it.

      You have to do something like Divide & Conquer optimization.

      Consider that you now need to precalc something for the interval [L;R] You should take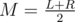 and calculate answers for queries [M;M], [M;M + 1], ..., [M;R] Calculate same thing for queries [M - 1;M - 1], [M - 2;M - 1], ..., [L;M - 1]

      Now you can answer any query [X;Y], such that X ≤ M ≤ Y if you can merge answers for [X;M - 1] and [M;Y] in O(1)

      Now we can deal with any query that consists M and we have to deal with intervals [L;M - 1] and [M + 1;R].

      We have wasted O(R - L) calculation time, so whole recursion will be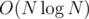

      I don't remember exactly how do we make it run in O(1) from this point, but should be possible with some bit manipulation.

      Here's the solution in :

      Note that you can do it like on a segment tree now, when you are in some node [L;R] and want to process interval [A;B] you need to either answer the query instantly if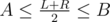 or whole interval [A;B] is in 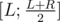or 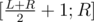so you can move here to answer query thus having O(h) time complexity, where h is

      Possible O(1) solution

      Hope this helps you!

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    There is a simple way of getting table for inverse of factorials partially avoiding inverse calculation. If you have n! - 1 then (n - 1) - 1 = n! - 1·n. n! - 1 can be either precalculated or calculated the normal way if you want O(n + q) instead of O(n + qlogn). I think there was some other method of calculating inverse for all numbers from 1 to n or their factorials in O(n) but it required a bit more of number theory knowledge to understand and I can't remember it.

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If mod is not very big, you can do it in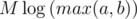 time where M = mod.

Here's link, but unfortunately it's only in Russian.

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

If (a < b) answer is 0, if (a == b) answer is (1 % MOD), otherwise Product(b+1, a) % MOD

Imagine you have number A, module M, and remainder C:

A % M = C
A / M = k
A = M*k + C
A * B = (M*k + C) * B
A * B = M*k * B + C * B
(A * B) % M = (M*k * B + C * B) % M
(A * B) % M = (M*k * B) % M + (C * B) % M
(M*k * B) % M = 0
(A * B) % M = (C * B) % M

Now you need a multiplication loop (b .. a] taking module on every step

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    if(a < b) answer isn't zero.

    For example, 5!/6!(mod 1e9+7) = 36166666920

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Sorry, than what does the exclamation sign means here? I thought that it's factorial:

      (5! / 6!) % (1e9 + 7) = 
(120 / 720) % (1e9 + 7) = 
( 0 ) % (1e9 + 7) = 0
      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        120 / 720 is not 0.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          It's not 0, but mathematical modulo operation is applicable only for integer division, so the answer must be integer

          By the way, in the condition, I think, that 'a' is meant to be 'n', and 'b' is meant to be 'm'. So there is a rule, that 1 <= m <= n, and (a < b) can be a valid input

          → Reply
»
8 years ago, # |
← Rev. 5   Vote: I like it -13 Vote: I do not like it

I gave a wrong answer! Sorry

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I don't get what Euler's Phi has to do with that, it's Fermat's theorem which has. And this works only if mod is prime.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Corrected, u are right.. Used the word phi by mistake

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +21 Vote: I do not like it

        and the word Euler

        → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it -26 Vote: I do not like it

...

→ Reply