Errichto's blog

How to solve this expected value problem, from Winter Petrozavodsk 2015?
By Errichto, 9 years ago, In English

I'm not able to find any link. I think that this problem was used in the last day of the camp (Petrozavodsk, Winter 2015). I didn't manage to solve it during the contest and I still don't see a solution.

Given n ≤ 106, find the standard deviation (or variance) of an, with allowed precision 10 - 6. A sequence a1, a2, ..., an is generated as follows:

a[1] = 1
for(int i = 2; i <= n; i++) {
	int j = rand(1, i-1); // random integer from interval [1, i-1]
	int k = rand(1, i-1);
	a[i] = a[j] + a[k];
}

I'm not sure about constraints but I think it doesn't matter (I would appreciate any polynomial solution). Also, maybe the answer was required modulo some number, instead of a real number with some precision — I don't know, sorry. And yes, the expected value is n.

  • Vote: I like it
  • +66
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Like for the tag "swistakkdidntwanttohelp" :)). I googled what standard deviation means and it gave me a headache. I'm more than curious how to solve this problem and I'll think at it. Thanks for sharing it with us. I hope someone will be able to solve it

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Yeah, googling it may be scary. The most important formula to know is:

    Var(X) = E[(X - E[X])2] = E[X2] - (E[X])2

    So, it's enough to calculate E[X2]. In other words, the task is to find the expected value of an2.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it -20 Vote: I do not like it

      Sorry for asking this, but can you, please, be more thoroughly? I really don't understand what Var (X) or E[X] means. Can you define them? I think it may be helpful (for me, at least) to know exactly what you are saying, because this is the kind of topic that may be met in a lot of problems.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        E[X] is the expected value of X, and Var(X) is something not very important to understand. Let's talk via PM, not to spam people.

        → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it -10 Vote: I do not like it

        Var(X) is dispersion, I think. We are learning about it on probability classes a lot of. It is something like what is variation between elements and expected value.

        For example: if you have function F(x)=x and have numbers 1,101. Expected value is 51 and dispersion is much bigger than if you have numbers 50 and 52 ( they are really close to expected value).

        → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +47 Vote: I do not like it

The problem is easier than you think :) It's a shame that we didn't manage to solve it during the actual contest. The solution is just to write down what you want to compute and then, well, compute it. The following description might not be accurate, but you should get the idea. I'll index n from 0, and let ξn be the random variable. For some reason \frac and \sum commands do not work, so everything is super-ugly:

dn = Dξn = Eξn2 - (Eξn)2

qn = Eξn2 = n - 2Σi, j < n [E(ξi + ξj)2] = n - 2Σi, j < n [E(ξi2) + 2E(ξiξj) + E(ξj2)]

sn = Σi < n qi, just partial sums

tn = Σi < n E(ξiξn)

rn = Σi < j < n E(ξiξj) = Σj < n tj, just partial sums

pn = Σi, j < n E(ξiξj) = 2rn + sn

Computing qn from sn and pn should be straightforward, so let's focus on computing tn.

tn = Σi < n E(ξiξn) = n - 2Σi, j, k < n E(ξi(ξj + ξk)) = n - 12Σi, j < n E(ξiξj) = 2n - 1pn

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 5   Vote: I like it +10 Vote: I do not like it

    Thank you very much! I've managed to implement it and the results are confirmed by the monte carlo method.

    In the last line you have a small mistake. It should be tn = ... = n - 22Σi, j, k < n E(ξiξj) = n - 12Σi, j < n E(ξiξj). And btw. rn turns out to be unnecessary. Anyway, thanks again!

    my code

    EDIT: hah, Codeforces keeps changing \n to n in my code.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      Corrected n - 1, thanks! I used rn because it was the most straightforward way for me. Good luck with the other problems of this contest :)

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I don't want to solve other problems from the contest. It's just that I didn't manage to solve this problem back then (during the camp) and I tried it again a few times since then. Finally, I really wanted to know how to solve it :)

        Though, I have many more problems waiting to be upsolved. I'm not good at telling myself to sit and solve some old hard problem. Inventing new problems is so much more interesting.

        → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Using the law of total variance, it's not hard to get this reccurence for fn = Var(an):

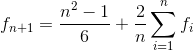
but I'm now sure if there is enough precision for n = 106. Should work fine if the answer is only required modulo prime.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    Could you please share your proof, or correct the formula? Because it seems like this one produces an incorrect output for n = 4 (the correct one is 16/9).

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      Oops, I thought all ai's are independent, but they are obviously not. I'm sorry :(

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        I'm not familiar with this theorem. Can you provide some example where it can be used? In something that could be a competitive-programming problem.

        → Reply
»
9 years ago, # |
  Vote: I like it -23 Vote: I do not like it

After going through post and all comments, I was like

→ Reply