Azret's blog

Trigonometry proof [CLOSED FAST :D]
By Azret, history, 8 years ago, translation, In English

Hello.

I am trying to prove that sin (α - β) = sin α * cos β - cos α * sin β but getting something wrong.

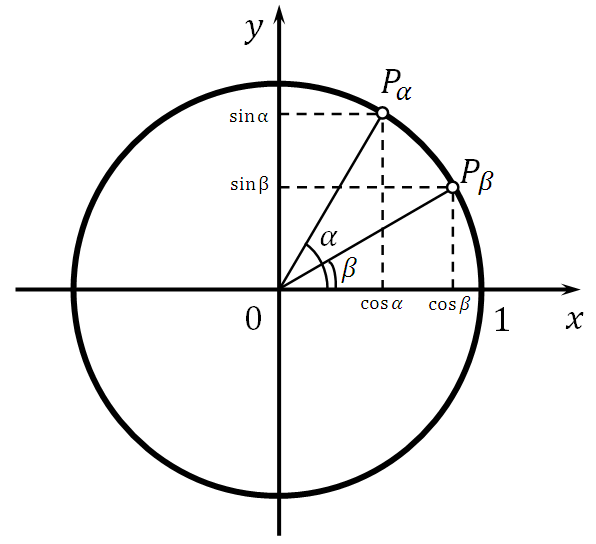
OPα = (cos α, sin α)
OPβ = (cos β, sin β)
|OPα × OPβ| = |OPα| * |OPβ| * sin (γ)
|OPα| = |OPβ| = 1
γ = α - β
Hence, |OPα × OPβ| = sin (α - β)
Since, |A × B| = Ax * By - Ay * Bx
|OPα × OPβ| = cos α * sin β - sin α * cos β
Hence, sin (α - β) = cos α * sin β - sin α * cos β

But all formulas in internet say that sin (α - β) = sin α * cos β - cos α * sin β , i.e reverse of what I wrote above. Can someone find my mistake?

P.S Below is the correct proof written in white. You can find my mistake yourself first. ;)
As I understood I made mistake in computing angle. Since angles are + in counter-clockwise direction then
|OPα × OPβ| = ... * sin(360 - γ)
|OPα × OPβ| = |OPα| * |OPβ| * ( - sin (γ))
Hence, |OPα × OPβ| =  - sin (α - β)
And  - sin (α - β) = cos α * sin β - sin α * cos β
Leads to sin (α - β) = sin α * cos β - cos α * sin β

  • Vote: I like it
  • +8
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

You take absolute value only from part of the expression. I think it should be:

|OPα × OPβ| = |OPα| * |OPβ| * |sin (γ)|

|OPα × OPβ| = |sin (α - β)|

And as result:

|sin (α - β)| = |cos α * sin β - sin α * cos β|

And that is correct.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    |A| is magnitude of vector A, not an absolute value. :D

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

as you know, A × B =  - B × A, and you made such a mistake in order of operands in following expression: |OPα × OPβ| = sin(α - β).

→ Reply