http://www.spoj.com/problems/FAILURE/
Problem is simple : N points are given in Euclidean plane. For each points, you should find the smallest distance between itself and other points, in respect of euclidean distance.
I had no idea on the solution of this problem (except Delaunay triangulation. I hope there's a simpler solution), so I googled for the solution : https://github.com/anurag-jain/spoj-1/blob/master/MLE.cpp but I still have no idea why it's O(NlgN).
Can someone help me with this problem? T.T
I believe this is simply a KD-Tree which is known for being able to find nearest neighbor in O(logN) on average per query.
Yeah, i solved this problem using a KD-Tree.
Some time ago I asked yeputons about that problem, because his team has solved it during virtual contest in 28th minute and it was his reply: "Hi there. We used a somewhat 'standard' randomized algorithm (code): take a random line, project all points to it. Then take point P, go simultaneously to both sides along the line and stop going when it's clear we won't encounter any closer point. I've heard it's something like O(n*sqrt(n)), but it's better to ask PavelKunyavskiy — he should remember more about that." Cute, isn't it :)?
Btw solution intended by authors is some modification of divide and conquer algo for finding closest pair of points.
Wow, I got accepted using that.
A while ago we got a similar problem on a Bulgarian competition and nobody solved it. The author had used KD Tree and I presumed that all problems of this kind are solved using that, hence I disliked them. That is until now, this randomised solution is just beautiful! Thank you for sharing it.
P.S.
On randomised tests it seems to be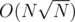
indeed, with quite a small constant. No clue why, though.
This is indeed quite cute. Is the O(n^1.5) bound easy to prove?
The reference solution was O(nlogn) and indeed was based on a divide and conquer. It is a bit more complicated than for the closest pair of points, because you cannot "prune" that much. I am a bit too lazy to write a full description but maybe this will be enough: consider a horizontal line dividing the points into two sets of similar cardinality. Solve the problem on the left and on the right. Then, for each point consider the intersection of its ball (centered at the point and of radius equal to the distance to the nearest point on the same side of the line) and the horizontal line. These intersections are just segments. Can many of these segments intersect?
Is there any link to a blog or editorial somewhere that explains it in more detail with proofs and such? It seems cool.
How do you ensure that you won't encounter any closer point ?
Let π be a projection to that random line. If for a fixed point P I looked at all points Q such that dis(π(P), π(Q)) < d, where d is the distance to the closest point discovered so far then I am sure I may stop looking since dis(P, R) ≥ dis(π(P), π(R)).
Excellent. Thanks!
EnumerativeCombinatorics describes a simple algorithm to find the closest pair of points in the plane. The same idea can be used to solve this problem.
I got stuck on this problem a while ago, and came across the following article: https://www.ri.cmu.edu/pub_files/pub1/moore_andrew_1991_1/moore_andrew_1991_1.pdf
Section 6.4 describes the algorithm, and the rest of the paper discusses some theoretical and empirical bounds on the runtime. They reference the following paper for a proof:
[Friedman et al., 1977] J. H. Friedman, J. L. Bentley, and R. A. Finkel. An Algorithm for Finding Best Matches in Logarithmic Expected Time. ACM Trans. on Mathematical Software, 3(3):209{ 226, September 1977.
which you can find here: http://www.slac.stanford.edu/pubs/slacpubs/1500/slac-pub-1549.pdf. I haven't had time to read it, but it seems highly technical, and makes certain assumptions about how the points are distributed.
There is an O(nlogn) solution without fancy structures. Not sure how well it will survive google translate, but here is my explanation: https://fajnezadania.wordpress.com/2016/07/23/na-wypadek-awarii/
I know you proved that in the end you only need to check a linear number of pairs between planes. But how do I choose those points? In the original divide and conquer algorithm, we take the last 6 points and the next 6 (if I am not mistaken). Can we take the same approach here?
edit: maybe I didn't get the translated version well and I am asking what's already explained in the article.
edit2: just realized the correct approach, thanks :)
edit3: it seems that i didn't. got TLE on SPOJ.