Author:danilka.pro.
Developed:I_Love_Tina,ThatMathGuy
We can try out all of the possible starting digits, seeing if we will go out of bounds by repeating the same movements. If it is valid and different from the correct one, we output "NO", otherwise we just output "YES".
Author:danilka.pro,I_Love_Tina
Developed:I_Love_Tina,ThatMathGuy
We can build a complete graph where the cost of going from point i to point j if |i - j| if ai! = j and 1 if ai = j.The we can find the shortest path from point 1 to point i.One optimisation is using the fact that there is no need to go from point i to point j if j ≠ s[i],j ≠ i - 1,j ≠ i + 1 so we can add only edges (i, i + 1),(i, i - 1),(i, s[i]) with cost 1 and then run a bfs to find the shortest path for each point i.
You can also solve the problem by taking the best answer from left and from the right and because ai ≤ ai + 1 then we can just iterate for each i form 1 to n and get the best answer from left and maintain a deque with best answer from right.
Complexity is O(N).
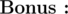 What if you have Q queries Q ≤ 2 × 105 of type (xi, yi) and you have to answer the minimal distance from xi to yi.
What if you have Q queries Q ≤ 2 × 105 of type (xi, yi) and you have to answer the minimal distance from xi to yi.
Author:danilka.pro,I_Love_Tina
Developed:I_Love_Tina,ThatMathGuy
Suppose we want to find the number of ways for a fixed n.
Let a, b, c, d ( 0 < a < b < c < d ≤ n ) be the number of chocolates the thieves stole. By our condition, they have the form b = ak, c = ak2, d = ak3,where k is a positive integer. We can notice that 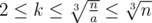 , so for each k we can count how many a satisfy the conditions 0 < a < ak < ak2 < ak3 ≤ n, their number is
, so for each k we can count how many a satisfy the conditions 0 < a < ak < ak2 < ak3 ≤ n, their number is 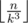 . Considering this, the final answer is
. Considering this, the final answer is 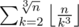 .
.
Notice that this expression is non-decreasing as n grows, so we can run a binary search for n.
Total complexity: Time ~ 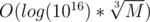 , Space: O(1).
, Space: O(1).
Author:I_Love_Tina
Developed:I_Love_Tina,ThatMathGuy
First of all it is easy to see that if we fix l then have 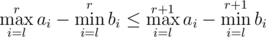 . So we can just use binary search to find the smallest index rmin and biggest index rmax that satisfy the equality and add rmax - rmin + 1 to our answer. To find the min and max values on a segment [l, r] we can use Range-Minimum Query data structure.
. So we can just use binary search to find the smallest index rmin and biggest index rmax that satisfy the equality and add rmax - rmin + 1 to our answer. To find the min and max values on a segment [l, r] we can use Range-Minimum Query data structure.
The complexity is  time and
time and  space.
space.
 What if you need to count (l1, r1, l2, r2), 1 ≤ l1 ≤ r1 ≤ n, 1 ≤ l2 ≤ r2 ≤ n and
What if you need to count (l1, r1, l2, r2), 1 ≤ l1 ≤ r1 ≤ n, 1 ≤ l2 ≤ r2 ≤ n and 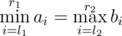 .
.
Hint:Take idea from this problem.
Author:I_Love_Tina
Developed:I_Love_Tina,ThatMathGuy
Let define the following propriety:if the point i is intersected by p segments then in our sum it will be counted 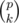 times,so our task reduce to calculate how many points is intersected by i intervals 1 ≤ i ≤ n.Let dp[i] be the number of points intersected by i intervals.Then our answer will be
times,so our task reduce to calculate how many points is intersected by i intervals 1 ≤ i ≤ n.Let dp[i] be the number of points intersected by i intervals.Then our answer will be 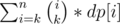 . We can easily calculate array dp using a map and partial sum trick,here you can find about it.
. We can easily calculate array dp using a map and partial sum trick,here you can find about it.
The complexity and memory is  and O(n).
and O(n).
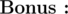 what if
what if 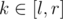 where l, r are given in input.
where l, r are given in input.
I'm really sorry that problem A was harder than ussually.










biggest solution ever for a div2 A
and safest
In Problem C, wasn't the upperbound of m 10^15 and not 10^16?
Yes, but the upper bound on n is 8*m if (k = 2 ). So the log(10^16) factor.
I didn't understand. Can you please elabore? Also, in the second C++ code given in the editorial , why has the upperlimit of the binary search been put to 1e15 instead of 1e15 ?
Lets take a particular value of
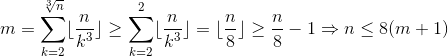
nand calculatemnumber of ways to steal chocolates. We will get something like this:so we can set
8*(m+1)as upper bound for binary search.So, why then is the upper limit in the binary search set to 5e15, instead of 8e15?
for k = 1e15, the answer is about 4.9*(1e15). That's why you can put limit to be 5*1e15.
What does log(10^15) mean? The upper bound is not clear to me.
See my comment above,
n <= 8*(m+1)and10^16is greater than8*(m+1)for anymthat satisfies input constraintsThanks!
BolsoMito
Contest was about to end, and I realized that I was solving bonus version of D... :(
Can D be solved in O(N) using two pointers?
You can use deque to find max/min + two pointer
Is there anybody who got AC for two pointers? I'm stuck with a bug right now and I don't know what I'm doing wrong.
I also thought that something like two pointers would help here. So I came up with this solution and got AC 18974188. The idea is to calculate in each iteration the number of segments that end at the current index and have max = min. I believe that it has O(N) complexity but can't prove it.
I think my code for problem A is easier to read than author code ==. sorry for my bad English http://codeforces.net/contest/689/submission/18925245
you're right about that,i added this solution to editorial,thank you.
Please, could someone help me. Why my solution for E is wrong on pretest 10?
18937604
I will be more careful with parenthesis next time.
Thank you so much
I used a different approach for the problem B. We can use a Segment Tree in order to get the nearest incoming shortcut in the range [i..N] and update the answer. O(N*log(N))... http://codeforces.net/contest/689/submission/18937575 Now I can sleep... I will read the tutorial after... Thanks a lot for the problems... Nice contest (Sorry for my poor English)
Actually you can run a simple bfs on the graph, since the graph edges cost only 1. You only have to know the levels of each nodes.
Yes. I know it now... But in the contest i don't realize it. I over killed the problem... :( . I submitted my solution 10 min after the contest has ended.
can you clarify more your solution by segments Tree ?
There is a greedy property in this problem, if you have two entry points (by shorcuts), you always must choose the leftmost point.
So you need to know the position of this point in the range [i..N] (that is why I used RMQ here).
Now for each point I update the answer with the minumum(distance to last point before, distance to the leftmost point in the range[i..N]).
Sorry for my poor english. I hope this helps you.
a super better code for A. https://ideone.com/Q5i7z6
Is it your idea?
yes! why?
Could you, please, explain it?
first if we are dialing a number, we make it mark true; then we check that if we have at least 2 number,1 in row up(1,2,3) and 1 down(7,9); then we check that if we have at least 2 number,1 in column right(1,4,7), and 1 in column left(3,6,9); if both our checks are true then no number can be made by directions like this,because this number is using the 3*3 up square so U can not shift the directions. and if U have any of(1,2,3) and 0 then U have a direction with length 4 and again U cannot shift the directions any way; i hope i have explained it good; sorry for bad English.
I have a doubt. Why are you checking against (7,9) and not (7,8,9)? Does this make any difference? Your logic is great by the way! :)
tnx:)
Explanation for A, If the given string (configuration) touches all four sides of keyboard, then answer will be "YES", else "NO". Upper side contains 1,2,3 , left: 1,4,7,0 , right: 3,6,9,0 , lower:7,0,9.
link : 18922768
what's the intended complexity for D? is O(n log(n) * log (n)) passable within the time. my program (which is O(n * log(n) * log(n))) fails in the 7th case :(
My solution run in ~250 ms,try maybe to use scanf.
solution run in ~250 ms,try maybe to use scanf.
I always use scanf for such huge inputs. maybe too much constant factor there
Yep I'm also having the same concern. I came up with an solution during the contest but its worst-case performance was ~2500 ms and gets TLE on pretest 7. That was driving me crazy. I tried getchar-based I/O and even function pointers (to digtinguish between min/max cases) but neither helped... Appears that the constant factor in my implementation is too large.
solution during the contest but its worst-case performance was ~2500 ms and gets TLE on pretest 7. That was driving me crazy. I tried getchar-based I/O and even function pointers (to digtinguish between min/max cases) but neither helped... Appears that the constant factor in my implementation is too large.
I totally forgot about sparse table RMQs during the contest... T^T Segment trees seem to consume really a lot more time than that, both when coding and running.
I had this problem too, but then i realized that ANS can be more than 1e+9. Got AC, now. And there can be TL because of you trying to get_ans separately (max/min) if you'll get it in one time. Sory for my english, code will show it better https://ideone.com/aRj0ti
Ah... Thanks for pointing out, I didn't even realize I could do that! _(:з」∠)_ And sparse tables can also be optimized in this way, if I got it right?
i think Sparce table can't get TL, because it works too fast :). So it is no need to optimize it by this way. It's all about constant factor in Segment Tree :/
Sparse table works O(1) per query, so I think there is no need to optimise it :D
thanks a lot
i got AC by querying (max(F,l,r),min(G,l,r)) at the same time
Thank you,I changed my segment tree to do exactly what you said!
Aha, I meet this occation too. And I put Update1 and Update2 together , then I get AC. Sorry for my sorry English.
I also use a o(nlogn^2) solution, binary search and segment tree. Luckily I passed case 7 in 1965ms but tle in case 61. Then I replaced __int64 with int in binary search and get accepeted. It's interesting that I passed case 62 in 1996ms~ But later again I submit my solution, it tle again QWQ.
Еverything depends on the phase of the moon.
Guys, as i understand, there are no solution for python 3 for task C? Maybe it is good to separate time limits for different languages? Does system have such possibility?
My python solution for A: here...
More pythonic:
Wow, I like the way binary search is implemented! Looks really neat!
Can anyone please explain the solution idea for problem D ? I have read the editorial but I can't get the idea :(
I do the following.
You will calculate the answer for each segment that starts in position L. So, you need to count how many positions i are that max(A[L],A[L+1],... A[i-1],A[i]) = min(B[L],B[L+1],... B[i-1],B[i])
Now, the key observation is that the function max doesn't decrease. Similarly, function min doesn't increase. If you draw both functions would be something like:
(-) is the min function.
(*) is the max function.
(+) is when both functions have the same value (what you are looking for).
Looking the drawing(imagine is a good drawing) you notice that the difference between min function and max function doesn't increase. First is positive, maybe at some moment it is zero and then will be negative.
So, you need to search in wich position (if exist) the diference between both functions is 0. I did two binary search, one for the last position where min(L,i)>max(L,i) andthe other for the first position where min(L,j)<max(L,j). if j>i+1 then there exist j-i-1 positions where both functions are the same.
You have to repeat this for each starting position L. Complexity is O(NlogN)
A typo :- Function max doesn't increase(decrease)
Sorry, fixed
Shouldn't it be O(n * logn * logn) as u have to query seg tree for min/max each bin search
make a sparse table . sparse build is O(nlogn) and query as O(1)
ok ! Tried it with seg trees in java TLE on test 7
It says it's O(logn).
it's funny that problem A has longer code than B,C,D,E!!
A lot of people solved it with codes similiar to mine: http://codeforces.net/contest/689/submission/18922407
What is wrong with my solution of Div2B: My solution
You are not considering back edges, that is, start to end and end to start.
Consider this case -
8
5 2 3 8 5 6 7 8
Correct answer is -
0 1 2 2 1 2 3 3
Also a[1000 * 1000] should be a[2000 * 1000+5]
Also, its O(N^2) and will give TLE
The problem states that a is a non-decreasing sequence...
Yes, right!
Correct example would be -
10
5 5 5 8 10 10 10 10 10 10
Here distance from 1 to 8 should be 3. The edge 5-> 4 should be considered.
Can anyone explain the first two approaches/codes for problem A ?
If the given string (configuration) touches all four sides of keyboard, then answer will be "YES", else "NO". Upper side contains 1,2,3 , left: 1,4,7,0 , right: 3,6,9,0 , lower:7,0,9.
link : 18922768
I have idea of BONUS D : with one element X of array a[] I find how many times this element is max of subsequence(define cntA[X]) and with one element X of array b[] I find how many times this element is min of subsequence (define cntB[X]) (use map to store cntA[] and cntB[]) Ans of problem is product of all (cntA[X] * cntB[X]); To find cntA[] (max of subsequence is the max value of subsequence and min index) let left[i] is the first element so that a[left[i]] >= a[i] and left[i] < i; right[i] is the first element so that a[right[i]] > a[i] and right[i] < i; cntA[a[i]] += right[i] — left[i] — 1; same with cntB[]
This has to be one of the hardest div2 contest I have ever seen... My first thought on problem B was like :"Nah it's just a Div2B, it can't be dfs/bfs related...", and there goes a bunch of time trying out a few naive approaches.
Problem D was pretty awesome, when I learnt data structures my underestimated Sparse Table and thought "Huh if it is static I would rather use a prefix array, and if it has updates I would use segment tree." What a back stab! Thankfully it wasn't that hard to learn at all after understanding BIT and segment tree.
I don't think div2A is too hard though, all you need is to make the observation that you can't slide the order of input as long as the input contains all four side of the boarders, it's not that straight forward but definitely not hard. In fact, I think it is pretty decent as div2A problems are getting more and more similar to each other.
Edit: Oh snap, just read the problem D editorial, dang it I done my research on Sparse table before coming up with the observation of binary search is again applicable in this problem... X_X
I think I have missed something huge in problem E... I am using the partial sum approach to keep the amount of points within a certain length of segment, but I somehow got tripped over by test 13.
http://codeforces.net/contest/689/submission/18942895
UPD: Heil long double.... AND PRAISE MODULAR INVERSE FUNCTION WHICH I'VE TOTALLY FORGOT
I also got wrong answer in test 13. Can you explain why we use modular inverse function?
oh, I misread D and came up with a complicated solution to find the count of max(a) == max(b)...
My solution for A http://codeforces.net/contest/689/submission/18930613. I check if i cant move all the digits to all the direction then it's a "YES".
http://codeforces.net/contest/689/submission/18956712
``
It's O(N^2).
hello friends can anybody help me in div2B in pointing out the mistake, i start visiting all the intersections from a node and update their distance(do this initially for 1) and also insert them all in a set and then for all other n's i just iterate over them and find their upper bound and lower bound and take its minimum distance and then do the same process as above. here's my code http://codeforces.net/contest/689/submission/18938871, although i am getting a wrong answer but i cannot figure out where
Try this
Your algorithm first visits 1 and goes to 5, and then goes to 6, then 7, ... until finally reaching 2 from 10. After that when
if (d[x]) return;is executed the program misses the fact that 2 can actually be reached within fewer steps.The order you visit points is not guaranteed to be correct, that is, when you visit a point and use it to update other points' information, you are not sure that the info on current point is fully determined (will not be updated in the future), which may lead to some incorrect answers. To ensure this you will need BFS in this problem's case, and Dijkstra's algorithm when dealing with a graph whose edge weights are not all 1. These approaches use a vertex's information to update others' only when they're sure the optimal answer for it has been fully determined.
Thank you for the reply but how can the input be 5 1 1 ..... , it should be in increasing order only according to the question and my answer is going wrong at 75th position, can you please recheck, thank you
Oh sorry that was such a careless mistake T^T I completely misunderstood the case. My apologies...
Your algorithm is mostly correct with a few errors. Firstly I suppose you're using
if (d[x] && d[x] <= v) return;and I know you can figure out why :)Let's directly observe test #4. The problem is with the 87th point — the program gets to 53 within 6 steps with the help of shortcuts, and goes through another shortcut to reach 87, with 7 steps taken. However there exists another solution: use shortcuts to get to 90 within 3 steps and then go back to 87 — that's only 6 steps!
What's wrong here is, when we iterate to 87,
if (*vis.lower_bound(i) == i) continue;ignores it, leaving the chances to be reached from some neighbouring points (in this case, 90). After removing this statement, you should also carefully handle cases wherevis.lower_bound(i) == vis.begin(), which could cause range overflows when applying the--operator.However the quickest and safest way to handle such shortest-route problems is doing a BFS. Hoping to be helpful this time (。・ω・) Correct me if I made some mistake again
How to find out the possible upper limit of n in Div.2 C? Trial and error?
You can use 1e18 as upper limit. It will pass all test cases. Or you can calculate answer for 1e15 (using upper limit 1e18). It will be upper limit.
Check the comment nagibator2005 above
What's the idea behind test 11 in D? My code can't pass it and I can't find the test it doesn't work on. Link: http://codeforces.net/contest/689/submission/18949949
In div 2 C — "how many a satisfy the conditions 0 < a < ak < ak^2 < ak^3 ≤ n, their number is floor(n/(K^3) )...how ?
For a particular k the max possible ak^3 to be stored in bag n is the greatest value of ak^3<=n
So no. of ways = a = n/(k^3)
Take eg n = 64 for k=2 values of a which satisfy are 1,2,3,4,5,6,7,8 count = 8 = (64/(2^3)) = (n/(k^3)) for k = 3 values of a which satisfy are 1(27),2(54) count = 2 = (64/(3^3)) = (n/(k^3))
Above brackets are floor since int. divison
For some strange reason, my submission to B with Dijkstra is faster than the submission using a BFS
I am not getting Prob D explaination. We binary search to find rmax and rmin for fixed l which satisfy the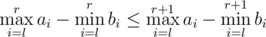 Or which should satisfy max ai — min ai
Or which should satisfy max ai — min ai
See my submission, I am getting WA at test case 3.
you know the inequality for sure because min is decreasing and max is increasing,consider function fl(r) = max a[l..r] - min b[l..r] then fl(r) ≤ fl(r + 1) so you can binary search to find rmin which is the minimal number such that fl(rmin) = 0 and rmax is the maximal number such that fl(rmax) = 0 then for each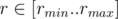 fl(r) = 0 so add to answer rmax - rmin + 1,be attentive with case when there doesn't exist any r for which fl(r) = 0.
fl(r) = 0 so add to answer rmax - rmin + 1,be attentive with case when there doesn't exist any r for which fl(r) = 0.
Can anyone explain how this code for problem D works? (Credits to szawinis)
It looks like he did something with a monotonic queue, or related.
If you want to understand this code first of all you need to understand how does a deque works.
Or here(read method 3)
In problem D I wonder what is the solution if both of them can tell only the maximum value?
My solution can solve it as well.
Assuming the number T appears in both sequence A and B, In A it covers ranges [la1,ra1],[la2,ra2]...(in every range T is the maximum) In B it covers ranges [lb1,rb1],[lb2,rb2]...(in every range T is the minimum) Set A consists of the former ranges, Set B consists of the latter ones.
If we take a look at the sub-ranges in A∩B, all the answers sharing the number T are included, and some don't share the same maximum/minimum,too. Then we exclude them.
Define F(A,B)=the numbers of sub-ranges in A∩B, let set ^A consist of all the ranges[la1,ra1],[la2,ra2]...excluding the position which has the value T.
Then employ the Inclusion-Exclusion Principle, the answer of same ranges sharing same maximum/minimum is F(A,B)-F(A,^B)-F(^A,B)+F(^A,^B)
Since for every value T,the number of its ranges in both A and B is O(its appear times), the total calculation can be done in O(N).
PS: Applogize for my imprecise description, you may as well view my code. In that I have just started to use C++ and there is much inherited from Pascal, it may not look great. :D
Can bonus of B be solvable by FLOYD warshal ? I think complexity is huge for this constraint O(N^3) => O((2x10^5)^3 ) => O(8x10^15) ? So what is the another approach ?
I think, segment tree + LCA would be enough?
** I meant to ask this as a question. Sorry for my bad English.
Please, describe your approach or stop throwing random guesses.
Why so difficult solution for A?
It could be done easier:
- (can up) all of "123" cells are free -> NO
- (can left) all of "1470" cells are free -> NO
- (can right) all of "3690" cells are free -> NO
- (can down) all of "709" cells are free -> NO
- otherwise -> YES
First solution that came to my mind and i think the safest one,whithout any cases.
how to solve bonus B and bonus D?
Can problem D simply iterate and compare A[i] == B[i], A[j] == B[j], and max(A[i], A[j]) == min(B[i], B[j]) when j = 1, i = j — 1?
I desperately wanna know why the above solution ends up with the wrong answer on hidden test cases.
wrong answer on hidden test cases.
wat?
What I meant was above method turns out wrong when submitted on test case #5
You can see all tests by just clicking on your submission.
What if all elements are equal?
See test:
3
1 1 1
1 1 1
You output 5 but the answer is 6: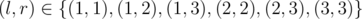 .
.
Solution for E: line sweep. For each point, if there's d intervals containing it, add Ck(d, k) to solution. 19035768
Can problem B be solved using Dynamic Programming??
see C++ with deque.
Could anyone explain O(n) solution for 689D - Друзья и последовательности?
How to solve problem E bonus? I thought of the following:
Let's have F'(x) = answer for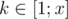 . Then obviously our answer will be F'(R) - F'(L - 1). But here comes the problem on how to count
. Then obviously our answer will be F'(R) - F'(L - 1). But here comes the problem on how to count 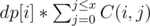 for every i. Can you please explain the official solution to the bonus (I_Love_Tina, ThatMathGuy).
for every i. Can you please explain the official solution to the bonus (I_Love_Tina, ThatMathGuy).
my first program of problem D is the bonus...hahaha. I misunderstand the problem, and then solve the bonus...