Hello, Codeforces!
The 23rd Central European Olympiad in Informatics ( CEOI ) will be held in Piatra Neamț, Romania (18. — 23. July 2016).
Offical website of CEOI 2016 : http://www.ceoi2016.ro/
The Central European Olympiad in Informatics is an annual informatics competition for secondary school students. Each of the participating central European countries sends a team of up to four contestants, a team leader and a deputy team leader.
You can find list of CEOI 2016 participants here.
The competition will take place on Wednesday July 20, and Friday July 22 2016, from 08:30 EEST to 13:30 EEST (05.30 UTC to 10.30 UTC). On both competition days contestants will be given three tasks to complete in the five hours.
The CEOI 2016 Online Competition will take place during the same competition hours. Posted tasks will be exactly the ones used during the real competition and will be graded using the same test data.
More information about Online contest can be found here.












Poland's team leader is Errichto cool!
"You have to wait 5 minutes between two consecutive submitions for the the same task."
Please say it's just for practice :(
Can people watch results online like on IOI? If not, when can we see the results?
So... Where are the tasks
Click upvote if you also want to kill authors of 5 min rule..
Would you prefer a full queue?
Where the tasks for the previous years ???
Well, 5 minutes rule and last submission (but not best) counts?
Seriously?
Unfortunately, the contest interface does not support taking the maximum score of all submissions. This was mentioned in the competition rules quite some time ago.
Regarding the 5 minute rule, we were very worried that a very long queue might be created in the grader. The submission time restrictions were smaller for the on-site competition (1 minute for only one task), but we expected a large amount of participants and submissions for the online version.
It seems the grader performed better than we expected. We are sorry for the inconveniences.
Please, someone post the results :D
Thanks and good job! Seems like for most of the contestants the first day was meaningless with those small differences.
Deleted.
How to solve ABC?
How to get some points?
B 51: dp[len][first][last] — number of permutations of length len with fixed first and last.
How to get non-zero points in C???
B 100:
Let's go from left to right a call following dp: dp[i][c1][c2][c3][c4] where c1, c2, ... are number of connected components of each type. Let's notice, that there are 4 types of components. Each component is a directed path with begin and end. Begin of a path can be simple verticle or begin of the full path. End of the path can be a simple verticle or end of the path. So we have 4 types of components.
When we calc dp for some verticle, we have 2 cases: edge from this verticle goes left or right from it. So we need just to check many cases of joining/creating components and get O(n^2) solution.
By the way, time limit for this problem is very strict, so I added some dirty hacks before my solution passed.
After contest I solved with very similar but faster dp: dp[val][group]. Group keeps number of connected groups so far. In a move either we can add current value as a new group or we can simply merge two already existed groups in (group * (group — 1)) ways with adding value 'val' between them. Also we may connect a group with L or R (leftmost or rightmost indexed ones) if val < cs or val < cf.
Code
Could you elaborate on what groups are and more about the solution in general? I can't seem to understand it.
Assume we are iterating i now. It means we added all values bigger than i to some groups. Group number will keep number of unordered connected components when we added all numbers i + 1 to n.
Groups will consist numbers in spesific order like (5-2-3-1-6). First value will be bigger than second and last will be bigger than the one before it (excepts the ones constist cs or cr). When we are adding new value we can merge two existed groups. So we will choose two groups a and b. Then merge them like (a)-i-(b). Or we can add it as a new group. After adding all values there must be one group. Also there are some details about cs and cr. When we are merging cs with some other group we only can merge it to right of it.
Maybe my idea is different because tl;dr and I don't want to spoiler myself, but basically it is: Forget jumps over the finishing point f. The remaining jumps form k connected sequences — groups — to the left of f and k (or k - 1) to the right of f.
My solution for probably hardest problem, C :
My idea was connected with xoring
Remember that xorall ^ firstXor ^ SecondXor = answer
So, if both guys count their xor and give it (somehow), its done.
We want to find such numbers A and B, that both A and B are in this set, and A operation B = C, where C is xor of all numbers given to one guy. Such pair may not exist, though. However, it's very likely that we WILL find an answer, unless we're given malicious test. There are N * (N — 1) pairs of possible xors which can be from interval (0, 2 * N)
To defend from malicious tests, do the following :
P = random_permutation_generated_from_input();
solveProblemForP();
RestoreAnswer();
The permutation cannot be random at all, as other guys have to know what it is. I used a generator depending on value N AND testID. Why it's important to add testID? If we get all binom(12, 6) possible tests in N = 6, this will surely fail, as we'll answer all tests anyway, even after transforming the sequence.
Okay, let's deal with a random test.
We can also use the fact, that we can output numbers in a certain order. If we fail to find answer for given xor K, let's try to find answer for K + 1, and output numbers in reversed order. Therefore, probability of failing lowers much.
I got 29 points and disturbing segfault somewhere.
I would be very grateful if someone shares his opinion about my sol.
Oh, please next time say it's not working, firstly.
It should be! MLE because of my failure != WA :P
Of course, it may work. But because of "random" solution we can't know the real verdict without MLE :(
Well.. It passes N = 6 subtask. IMO this is the worst case for my algorithm, as probability of finding given XOR only raises. I'm not saying it would get 100, I just want to get some info from jury or more skilled guys :)
Reyna found one stupidity in solution above. Can I upsolve somehow?
It sounds like you change "failing for sure" to "failing with some probability". If this hack makes sense at all, I think the probability of failing isn't negligible. Otherwise your reasoning "why it's important" doesn't make sense.
I don't like that you care about xor of numbers. For me, looking for the sum modulo 2n + 1 sounds better. Giving some info for xor should be harder because there are more possible values. Am I right or not?
I'm not describing my solution simply because I don't know any nice solution for small n. (I could solve n ≥ 12 only.)
Let's assume my code fails for N = 6 with 1,2,3,4,5,6. So I want to get rid of this permutation and transform it into some other. However, if my "randomGenerator" was always transforming permutation to another one, then when I get all permutations, some other will for sure transform into 1, 2, 3, 4, 5, 6.
I also thought about modulo sum. This is better for one test, but I didn't find a good way to randomize the permutation modulo without modular division for non-prime N (there are still tests on which this idea fails).
Yeah, xor isn't so good because it can be unnecessarily big. Also, symmetric operations aren't so good.
This seems to me like a problem in which you try to make a random number generator that takes two arguments and has a very smooth distribution even for small numbers — with N(N - 1) possible pairs of arguments, it should cover all numbers in the range [0, 2N], so it's always possible to send the sum modulo 2N + 1 using just some pair of cards.
I didn't have the time to try out more complex options in the online contest (I started 3 hours into the contest, "competed" for ~1.5 hours and decided I'm too hungry to code more), but I'd try some higher order asymmetric polynomials with random coefficients modulo 109 + 7 (and then modulo 2N + 1).
Surprisingly, the case N = 6 is the hardest :D
UPD: Good news everyone! For N = 6, sending cards x, y such that P(x, y)%(2N + 1) is the sum of all assistant's cards works for P(x, y) = (ax + by)%(109 + 9), p = 27836604, q = 21425728. Tested on 200000 random test cases. I found those parameters after trying out several tens of thousands p, q and different randomisation formulas; you can find your own for this and larger N.
Hello! I am the author and problem setter of task Trick.
There is a clean and deterministic linear-time solution. After the second competition day, there will be a short session with the contestants where all task solutions will be presented. I will publish the solution for this task after the official session.
Meanwhile, why not enable upsolving on the online judging system or at least upload the test data?
I will try to sketch the main idea of the official solution here.
We need to find a (2N + 1) × (2N + 1) matrix with elements in the range 0..2N. Each element of this matrix represents the sum to which a pair of cards (a, b) is mapped to (except the main diagonal values, which don't make sense in the problem context). Thus, a pair (a, b) is mapped to the sum modulo 2N + 1 of the cards received, which allows to easily find the missing card.
We will use a constructive algorithm. We define an equivalence class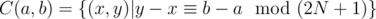 and let the pair (a, b) be a fixed representant of this class. We will map (a, b) to sum 0,
and let the pair (a, b) be a fixed representant of this class. We will map (a, b) to sum 0, 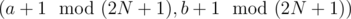 to sum 1 etc. This way, every pair within the same equivalence class is mapped to a different sum. Also, a pair belongs to exactly one equivalence class.
to sum 1 etc. This way, every pair within the same equivalence class is mapped to a different sum. Also, a pair belongs to exactly one equivalence class.
Now, we need to choose the class representants in a manner which allows us to prove the correctness of the protocol (that it will work for any of the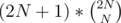 possible test-cases).
possible test-cases).
By starting from an intuitive set of representants ((0, 2N), (1, 2N - 1), (2, 2N - 2), ..., we reach a point in the proof where a condition that must hold is very close, but not yet there. This gives us the idea to change the protocol only slightly, leading us to the following representants: (1, 2N), (2, 2N - 1), ..., (N - 1, N + 2) (a total of N - 1 pairs), to which we add special pairs (0, 1), (0, 2N), (N, 2), (N, 2N - 1), (4, N + 1), (2N - 3, N + 1) (these pairs will be chosen for odd N; if N is even, in order to keep the required properties, we simply swap the numbers in the first N - 1 pairs, leading to (2N, 1), (2N - 1, 2), ...).
A more detailed analysis and proof will be published on the competition site in the following days.
There are many approaches to this problem, many of them leading to 29 points. Indeed, solving for large N is pretty easy, as there are many heuristics that can't be failed with a reasonable amount of test-cases. The case for N = 6 is also solvable in many ways (the first test contains all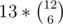 possible test-cases, so 29 points means the given protocol is actually correct for all possible situations). The critical part of the problem is solving N = 10..30, because this is big enough to not be solvable with backtracking or other brute approaches, but also small enough to not be solvable with heuristics.
possible test-cases, so 29 points means the given protocol is actually correct for all possible situations). The critical part of the problem is solving N = 10..30, because this is big enough to not be solvable with backtracking or other brute approaches, but also small enough to not be solvable with heuristics.
Thanks for sharing the approach :)
The correctnes of the protocol is REALLY not obvious. The solution above can be expressed in one sentence — create a protocol through which we will be able to code any modulo sum using given values. Creating such protocol = magic. Waiting for proof :)
As I promised, I will post a more detailed proof and explanation of the solution.
In addition to the previous description, the idea was to find a matrix which had the secondary diagonal filled with zeroes, the diagonal below it filled with 1's etc. (this is the protocol with class representants (0, 2N), (1, 2N - 1), ..., (N - 1, N + 1).
Let's try to prove the correctness of this protocol. Assume we receive the cards C1, C2, ..., CN which sum up to a fixed number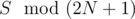 . From each of the pairs
. From each of the pairs 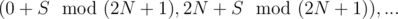 we can receive at most one card (otherwise, we would receive a valid pair to encode the sum). This means we can receive, in total, at most N + 1 cards (because the considered pairs and the card N make a complete partition of the set {0, 1, ..., 2N}). This isn't strong enough; if we would have gotten at most N - 1, we would reach a contradiction and complete the proof. However, the difference from N + 1 to N - 1 is small and this hints us that we should only change this protocol slightly (especially since there are many unused pairs). I believe there are other ways to "fix" this broken protocol, the one I found is only an example.
we can receive at most one card (otherwise, we would receive a valid pair to encode the sum). This means we can receive, in total, at most N + 1 cards (because the considered pairs and the card N make a complete partition of the set {0, 1, ..., 2N}). This isn't strong enough; if we would have gotten at most N - 1, we would reach a contradiction and complete the proof. However, the difference from N + 1 to N - 1 is small and this hints us that we should only change this protocol slightly (especially since there are many unused pairs). I believe there are other ways to "fix" this broken protocol, the one I found is only an example.
Now, to prove the correctness of the second protocol, we use the same reasoning. However, this time we can take at most one card from each of the triplets (0, 1, 2N), (2, N, 2N - 1), (4, N + 1, 2N - 3) (3 cards) and at most one card from each remaining pair (N - 4 cards). Since these pairs and triplets make a complete partition of the set {0, 1, ..., 2N}, this means we can receive at most N - 1 cards, which leads to the required contradiction and the proof is complete.
Additional notes: the protocol is valid, in the sense that all pairs in the same equivalence class are distinct (both numbers in the pair are added to a different sum), and no pair of cards belongs to more than one set (because every set is defined by the b - a difference, and analyzing those differences for the considered equivalence classes, they are all distinct).
Can someone drop me a hint how to do A? Can't get down from N^2/2 queries in worst case scenario.
First, find a way to split the vertices into two disjoint sets such that the (new) edge is surely between them, in O(lgn) time. You may want to use the disjoint set data structure for this task (since you have to be sure that whenever you add a node, you also have to add the entirety of its component, coupled with a somewhat obscure trick — using the binary representation of the vertices to find the given split. This might sound slightly off — it sure did for me, but I found no other way to solve this part. Then, implement two binary searches on the sets, narrowing down the possibilities until only two nodes remain. Those nodes are, of course, the answer. The key idea is to test which of the halves contains the edge, which can be done with only one call to the grader query function. This particular solution, given a clean implementation for the first part, has an upper bound of 3 * n * lg(n) calls to query. I could gladly give more details if you wanted to, but you asked for just a hint.
Best of luck, and have fun!
can you elaborate a bit on how you used binary representation to find the two disjoint sets?
or share you code please
Is it possible to submit solutions somewhere?
Or test data?
http://cni.nt.edu.ro:8080
Ehm, that was about upsolving the problems from the 1st day. Linking to the 2nd day online contest isn't very helpful.
Again, please?
That will take maybe an hour. The contest barely ended.
Why an hour, I saw photos from the first day a few minutes after it ended?
I was shown that there's an hour remaining when the contest ended. WTF?
Probably they used the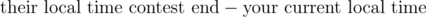 formula or something.
formula or something.
That explains why I had 00:00:00 remaining time for the whole contest :D
So it's more like max( 0, their contest end — your contest start). I can't decide what's the worse mistake, this or seeing stuff like "contest ends in: minus 3 hours!".
http://codeforces.net/blog/entry/46065?#comment-306168
B. dp[len][cnt] — we divided first len tests into cnt subtasks.
Notice that cnt_of_full_rows(l, r) <= cnt_of_rull_rows(l + 1, r).
Using this fact, let's fix cnt_of_full_rows (only 50 unique values) and call it x.
Then, we can a find a segment [l, r] such that cnt_of_rull_rows(i, len) = x for all i in [l, r]. (this will be always a segment because cnt_of_rull_rows is non-decreasing).
Now, our DP became easier
which can be written like this
Wow, this is line equation. :)
Notice that x <= 50 and pre-calc line equation value for each x and line i in res[x][i].
Now, we need to find minimum on segment, which can be done with segment tree.
Total it is O(TN^2logT)
My code
My solution was basically the same (100 on the onsite competition), but I thought that it may be too slow so I solved the minimum range queries in O(union find complexity) instead of O(log). Did your pass in time?
It was TL when I did segment-tree recursively. But the code above got 100.
I was told that instead of taking minimum in segment [l, r] we can just take in prefix [1, r].
UPD. Too late xD
I solved it in O(NST) almost same as your solution using partial minimum.
In fact you can do query on prefixes, not on segment, because values on the left to the segment can never be less, than answer, because in fact there are less people, who get this group passed there. So you can just calc prefix minimums.
We can get rid out of the segment tree by modifying the solution a bit. Just notice that the result won't change if turn each requested segment into a prefix. It's not easy to show without a drawing, but let me have a try.
In fact, we can find a segment
[l, r]that cnt_of_full_rows(i, len) ≤ x for alliin[l, r](inequality instead of equality). Then, of course, l = 1. Of course, we want to minimize the value ofdp[len][cnt], so if we include alsodp[pos][cnt - 1] + (s[len] - s[pos]) * xwithxa bit too large (larger than the count of full rows), the result won't change.This thing means that we can do something like O(N) parallel "two pointers tricks", which turns the single
dp[i]computation time to O(NT) and then whole solution running time into O(TNS).Edit: huh, should have typed faster. xD
A: This is what I had at these weird wrong n ≤ 106 and TL=0.1s bounds. It worked locally in 0.09s, so it'd be a close call...
Checking if the whole word is okay is easy — just greedily maintain a stack and when seeing consecutive letters, try to pair them with the top of the stack. If they do, they both disappear; in the opposite case we must push it on the stack. Using that, we make an easy O(n2) algo.
However, we can tell something stronger — find all substrings which are correct under the task requirements. I'm not showing this, but just look what the stack looks like between all characters (also, before the first character and the last character). I say that a substring is correct iff the stack contents before and after reading it were the same (it's quite easy to prove).
Okay, so let's find all the equivalence relation classes between the points in time (equality holds when in two points of time the contents of stack were the same). It's easily doable with a trie, however under the limits above it was either too slow (O(n|Σ|)) or took too much memory (O(n) time, but ~400 megs of RAM). Hash-tables in nodes made probably no sense as they would be slow, too. What I did what some string hashing with a self-written hash-table, which gave me expected O(n) time and O(n) memory.
Now let's become greedy again. Write a recursive function which tries to place the first pair of parentheses (the one in which the opening bracket is on the beginning of the word). You can prove that the matching closing parenthesis should be placed as far as possible — that is, its contents should begin with some stack state α and should end with the same state α and the terminating α should be the last possible one. It can be done with some binsearching. When we place the brackets, we fire up recursively: between the brackets, and then to the right of brackets. We see that it's and might be too slow (you see the limits, right?)
and might be too slow (you see the limits, right?)
However, notice that the order in which we process the recursive calls does not matter. In fact, we can process them from right to left using some sweeping. For each state α we maintain the furthest possible occurence of α in the word. When we cut off the letters of the word, we find (in constant time) what state we just cut off and what's the second furthest possible occurence of it. When we process a 'recursive call', we do it in constant time (no binary search needed) and then put the recursive calls into the structure holding them. As a call is a subinterval of [0, N], we can hold them in a table. Putting a call is thus also O(1). So... overall, we get O(n) expected running time.
Then I submitted it, saw 0.008s on final tests. Aaaand mere minutes later got announced that n ≤ 105. Eh.
You win. What an awesome solution for a problen with wrong time limits and input size.
My 100pt solution:
Let's say that the answer isn't -1, that can be checked easily. For every suffix of the string (processed from last to first), we'll try to find the first point
nxt[i]where the greedy stack algorithm would empty the stack. How? By bruteforce iteration — for the i-th suffix, we'll start withx =i+1and iteratex -> nxt[x]+1(jump over points where the stack would contain just i) untilS[x]=S[i].Then, we'll match the first letter's bracket to the last possible position and recurse (same as in your solution). How? By bruteforce iteration — for a range [i, j), start with
x =nxt[i]and iteratex -> nxt[x]as long as possible for x < j. Then, positions i and x should have matching brackets.That second part is clearly O(N2) for a sequence of N
a-s (tested). However, it passes in 0.016 seconds worst-case. Weren't the test data kind of weak?IOW, you didn't need to put in all that effort :D
Can someone post the official results?
Here are the competition results:
Page 1
Page 2
Does anyone know when...
1) official editorials
2) the test data
...are going to be published?
Bump. The online judge is down and the test data / problem statements / solutions haven't been posted.
Also, I passed everything except one test on Kangaroo with an O(N3) solution :D
We have discovered a probable bug in the grader for ICC problem from the first day. Can anyone suggest a method for contacting organizers or problem's author?
Consider the following exerpt from the interactive player, which generates test for the participant on-the-fly:
Here
UniteVerticesfunction is called whenever the grader decides to fix an edge,selected_edgescontains list of all such edges (it's used for answering future requests) andcomponentis an identifier of a component of currently built graph.The problem is that at the time
selected_edgesis called,aandbare not the original vertices anymore, thereforeselected_edgesno longer contain "real" added edges (only some equivalents of them), hence the grader can give contradictory answers, which happened to one of our participants.The fix is to move the last line of the function to its very beginning.
Oh my god. I finally understand why the first problem was failing for me. I've spent the whole first day debugging because my "bruteforce" solution for the first problem was getting 0 points for the easy subtask and I was seriously confused. It was very straight forward but it was still failing for some reason and I couldn't focus on anything else.
Now I can rest in peace thanks to you.
MLC!
Can you explain what "MLC" means please? I've seen it in multiple places, but I don't know its meaning :(
It means: My Love for Comisia!
Another problem: solution for problem "popeala" from the second day is missing. PDF is here, but it describes something unrelated to the problem.
Does anyone have a solution description?
Hi, i am the author of problem Popeala. I don't know why the solution for another problem was uploaded. I will post the official solution which was supposed to be there (and sorry for the late response :) ):
D[t][g] = the minimum cost we can obtain if we take the first t test cases and put them in g groups.
D[t][g] = min(d[k][g – 1] + group_cost(k + 1, t)), where k is the last test of the previous group and group_cost(x, y) is the total score the participants will obtain on tests x-y if we group them.
The complexity is O(T * T * S) but it is too big for 100 points. Let’s assume that we are at test t. Let’s keep for each of the N participants the most recent test he failed and denote it with last. For contestant x, last[x] = max(k), k <= t and x failed test k.
Using those N values, we will divide our tests in N + 1 groups. Group 1 consists of all test cases from the most recent last[x] until t (basically, no one fails any tests in this group). Group 2 consists of all test cases from the second most recent last until the most recent last (only one participant fails the groups), etc. Let’s denote for each group x: best[x] = k, where k is the best option we can select for our dynamic programing with the restriction that k to be a test from group x. Formally: d[k][g – 1] + group_cost(k + 1, t) is minimal for all k from group x. If we know for each group this best, we will have to check only O(N) different possibilities ( since there are only N groups) and take the best option.
Let’s assume that we solved D[t][g], formed all the groups and computed each best[x]. Let’s see what happens when we go to test t + 1. Assume initially that all participants pass this test. One of the key observations is that the "best" values does not change (all options increase with the same value in the same group), so we just have to recheck all the N + 1 possibilities. Now let’s assume that contestant x fails test t + 1. The main modification is that last[x] becomes t + 1, so the groups change their configuration:
1) The previous last[x] was dividing 2 groups which now have merged into one. To compute the new best of this new group it is enough to just compare the two old options and take the best one.
2) All the options from the previous last to the new one change their value in the recursion. Unfortunately, it is necessary to loop throw all of them again since they changed drastically. Fortunately, we can do that brute force and the complexity will not change (because a passed test will be recomputed only once between 2 consecutive failed tests) The final complexity is O(T * S * N).