Разбор задач Educational Codeforces Round 14

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

691C - Экспоненциальная запись

Задачу предложил пользователь blowUpTheStonySilence.

Эта реализационная задача. Нужно было сделать ровно то, что написано в условии задачи. На мой взгляд, проще всего было найти позицию первой ненулевой цифры и позицию точки. Разность этих двух позиций равна числу b (если значение положительно нужно вычесть единичку).

Решение на C++

string s;

bool read() {
	return !!getline(cin, s);
}

void solve() {
	int pos = int(find_if(all(s), [](char c) { return c != '0' && c != '.'; }) - s.begin());;
	size_t dot_pos = s.find('.');
	if (dot_pos == string::npos) {
		dot_pos = s.size();
	} else {
		s.erase(dot_pos, 1);
	}

	int expv = (int) dot_pos - pos;
	if (expv > 0) expv--;
	forn(t, 2) {
		while (s.back() == '0') s.pop_back();
		reverse(all(s));
	}
	if (sz(s) > 1) s.insert(1, ".");
	if (expv == 0) printf("%s\n", s.c_str());
	else printf("%sE%d\n", s.c_str(), expv);
}

Сложность: O(n).

691D - Свопы в перестановке

Задачу предложил Zi Song Yeoh zscoder.

Рассмотрим граф из n вершин, рёбрами которого являются заданные пары позиций. В каждой компоненте связности этого графа мы можем поменять значения в любых двух позициях. Соответственно мы можем все значения отсортировать в порядке убывания. Легко видеть, что полученная перестановка является лексикографически максимальной.

Решение на C++

const int N = 1200300;

int n, m;
int p[N];
pti a[N];

bool read() {
	if (!(cin >> n >> m)) return false;
	forn(i, n) {
		assert(scanf("%d", &p[i]) == 1);
		p[i]--;
	}
	forn(i, m) {
		assert(scanf("%d%d", &a[i].x, &a[i].y) == 2);
		a[i].x--, a[i].y--;
	}
	return true;
}

bool used[N];
vector<int> g[N];
vector<int> perm, pos;

void dfs(int v) {
	if (used[v]) return;
	used[v] = true;
	pos.pb(v);
	perm.pb(p[v]);

	for (auto to : g[v]) dfs(to);
}

int ans[N];

void solve() {
	forn(i, n) {
		g[i].clear();
		used[i] = false;
	}

	forn(i, m) {
		g[a[i].x].pb(a[i].y);
		g[a[i].y].pb(a[i].x);
	}

	int cnt = 0;
	forn(i, n)
		if (!used[i]) {
			cnt++;
			pos.clear();
			perm.clear();
			dfs(i);
			sort(all(pos));
			sort(all(perm), greater<int>());
			forn(j, sz(perm))
				ans[pos[j]] = perm[j];
		}

	forn(i, n) {
		if (i) putchar(' ');
		printf("%d", ans[i] + 1);
	}
	puts("");
}

Сложность: O(n + m).

691E - Xor-последовательности

Задачу предложил Zi Song Yeoh zscoder.

Пусть z_ij — количество xor-последовательностей длины i с последним элементом a_j. Пусть g_ij равно 1 если 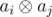$\text{[math]}$ содержит количество единиц в бинарном представлении кратное трём, и равно 0 в противном случае. Расмотрим векторы чисел z_i = {z_ij}, z_i - 1 = {z_{i - 1, j}} и матрицу G = {g_ij}. Легко видеть, что z_i = G × z_i - 1. Соответственно, z_n = Gⁿ × z₀. В силу ассоциативности операции матричного умножения можно сначала вычислать Gⁿ бинарным возведением в степень матрицы и затем умножить полученную матрицу на z₀.

Решение на C++

const int N = 101;

int n;
li k;
li a[N];

bool read() {
	if (!(cin >> n >> k)) return false;
	forn(i, n) assert(cin >> a[i]);
	return true;
}

const int mod = 1000 * 1000 * 1000 + 7;

inline int add(int a, int b) { return a + b >= mod ? a + b - mod : a + b; }
inline void inc(int& a, int b) { a = add(a, b); }
inline int mul(int a, int b) { return int(a * 1ll * b % mod); }

int count(li x) {
	int ans = 0;
	while (x) {
		ans++;
		x &= x - 1;
	}
	return ans;
}

void mul(int a[N][N], int b[N][N], int n) {
	static int c[N][N];
	forn(i, n)
		forn(j, n) {
			c[i][j] = 0;
			forn(k, n) inc(c[i][j], mul(a[i][k], b[k][j]));
		}
	forn(i, n) forn(j, n) a[i][j] = c[i][j];
}

void bin_pow(int a[N][N], li b, int n) {
	static int ans[N][N];
	forn(i, n) forn(j, n) ans[i][j] = i == j;

	while (b) {
		if (b & 1) mul(ans, a, n);
		mul(a, a, n);
		b >>= 1;
	}

	forn(i, n) forn(j, n) a[i][j] = ans[i][j];
}

void solve() {
	static int a[N][N];
	memset(a, 0, sizeof(a));
	forn(i, n) {
		forn(j, n)
			a[i][j] = count(::a[i] ^ ::a[j]) % 3 == 0;
		a[i][n] = 1;
	}

	//forn(i, n + 1) clog << mp(a[i], n + 1) << endl;

	bin_pow(a, k, n + 1);

	int ans = 0;
	forn(i, n + 1) inc(ans, a[i][n]);
	cout << ans << endl;
}

Сложность: O(n³logk).

691F - Couple Cover

Задачу предложил Michael Kirsche mkirsche.

Будем считать количество пар с произведением меньшим p. Получить количество не меньших, можно вычитая из общего количества пар n·(n - 1) количество меньших. Пусть cnt_i количество чисел в a раных i, а z_j — количество пар из a с произведением равным j. Для подсчета массива z можно воспользоваться по сути решетом Эратосфена: переберём первое число a, а также кратное ему b = ka и увеличим z_b на величину cnt_a·cnt_k. После предподсчёта массива z достаточно предподсчитать массив его частичных сумм, чтобы отвечать на запросы о количество пар меньших p.

Решение на C++

const int N = 3100300;

int n, m;
int a[N], p[N];

bool read() {
	if (!(cin >> n)) return false;
	forn(i, n) assert(scanf("%d", &a[i]) == 1);
	assert(cin >> m);
	forn(i, m) assert(scanf("%d", &p[i]) == 1);
	return true;
}

int cnt[N];
li z[N];

void solve() {
	memset(cnt, 0, sizeof(cnt));

	forn(i, n) cnt[a[i]]++;

	fore(a, 1, N) {
		if (!cnt[a]) continue;
		for (int b = a; b < N; b += a) {
			if (b / a != a) z[b] += li(cnt[a]) * cnt[b / a];
			else z[b] += li(cnt[a]) * (cnt[a] - 1);
		}
	}

	fore(i, 1, N) z[i] += z[i - 1];

	forn(i, m) {
		li ans = li(n) * (n - 1) - z[p[i] - 1];
		printf("%lld\n", ans);
	}
}

Сложность: O(n + XlogX), где X — наибольшее значение в массиве p.

Комментарии (11)

Показать архивные | Написать комментарий?

anh1l1ator

8 лет назад, # |

← Rev. 2 →

For problem D,

Though not necessary , even has a larger complexity and even dsu can be used in a better way to lower complexity I always wanted to use some kind of heuristic in my code 19211367.

Got WA in contest due to some minor major mistake( A mistake that is so minor but changes everything you are doing :P ).

→ Ответить

Golovin

Вопрос по задаче 691D: Как можно доказать, что в связном графе всегда можно отсортировать вершины?

Qwerty132

8 лет назад, # ^ |

Попробуй доказать это пузырьковой сортировкой. Принцип абсолютно такой же

DigitalArtistKz

In case someone faced the same issue. For problem E, my O(n3logk) solution in C# was getting TLE, so I parallelized matrix multiplication and got AC. 19309384

Lo_R_D

Е можно решать и двоичным подъёмом.

m4tt.kerin

Apologies all for what is probably a silly question.

The solution to 691D includes the line: const int N = 1200300; pti a[N];

I can't find any documentation for a pti datatype. I assume this is an abbreviation commonly used in codeforces solutions? If so can someone link me to an explanation of what this is? Or a solution where the abbreviation is defined.

ffao

I had never seen this abbreviation before, but looking through Edvard's submissions, for example, 19489538 you can see it means pair <int, int>.

thienlongtpct

I think that problem 691D - Swaps in Permutation have the same concept as problem 500B - New Year Permutation. I use dsu to solve both of these two problems.

Anyway, D is still very good problems I think so. Thanks zscoder.

AliShahali1382

6 лет назад, # |

I think the complexity of problem D is wrong. did you mention the sorting complexity?

p__ce1052

4 года назад, # |

why the answer for "mm" is NIE in problem B? isn't "mm" symmetric by the middle? or is it should be odd length string? from where can i infer that from the passage?

drinkWater.

4 года назад, # ^ |

Right top corner of 'm' is round but left top corner of 'm' is not round. That's why "mm" is not symmetric.

Блог пользователя Edvard

691A - Берляндская мода

691B - s-палиндром

691C - Экспоненциальная запись

691D - Свопы в перестановке

691E - Xor-последовательности

691F - Couple Cover