shubhamgoyal__'s blog

Problem on Möbius function
By shubhamgoyal__, history, 9 years ago, In English

Can somebody please explain how to use the Möbius function to solve this problem. https://www.hackerrank.com/contests/w3/challenges/gcd-product

  • Vote: I like it
  • +21
  • Vote: I do not like it

»
9 years ago, # |
← Rev. 4   Vote: I like it +23 Vote: I do not like it

Let f(n,m) denote the number of pairs (x, y), such that x ≤ n, y ≤ m, and gcd(x,y) = 1. WLOG, assume n ≥ m

Using inclusion exclusion,

If we store an array of prefix sums of mobius function, then f(n, m) can be calculated in .

Now let G(g, n, m) be the number of pairs (x, y), such that x ≤ n, y ≤ m, and gcd(x, y) = g.

Clearly,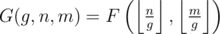 . There are clearly different values of this for all the g's

Our required answer is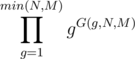 . Considering the different ranges in which G(g, n, m) is same, this can be calculated in O(n).

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +20 Vote: I do not like it

I solved it little differently. After the step

ans = Πg = 1pow(g, |{(p, q): gcd(p, q) = g}|)

Now I define a function f, such that for any prime p, f(pa) = p else f(n) = 1. It must be noted that

g = Πd|gf(d)

, Now If I substitute this expression in above expression and rearrange the multiplication we get

ans = Πx = 1pow(f(x), |{(p, q): gcd(p, q)%x = 0}|)

which reduces to

ans = Πx = 1pow(f(x), (n / i)(m / i))

. Now this is very simple to evaluate.

→ Reply