How to calculate 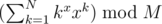 ?
?
Constraints are 1 ≤ N, M ≤ 2 * 109, 1 ≤ x ≤ 50 and time limit is 1 second.
Please can someone help?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
How to calculate 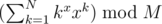 ?
?
Constraints are 1 ≤ N, M ≤ 2 * 109, 1 ≤ x ≤ 50 and time limit is 1 second.
Please can someone help?
| Name |
|---|



Auto comment: topic has been updated by Mamedov (previous revision, new revision, compare).
An O(x^2) solution is described here: https://www.hackerrank.com/contests/infinitum-mar14/challenges/summing-the-k-n-r-series
In our case modulo M is not a prime, it can be any number, but by this way we will need to calculate modular inverse.
It can be solved using "divide and conquer" approach.
Assume you try to calculate
In the last sum
It's clear that it's need to calculate sums
Than use "divide and conquer" approach to calculate all this sums for N, first calculate this sums for N/2 and than use the above formulas to calculate sums for N.
Thanks a lot sokian. I got this idea.
Specifying the time constraint would be nice. :)
I think sokian's approach will be O(x2log(N))
Auto comment: topic has been updated by Mamedov (previous revision, new revision, compare).
In what judge is this problem available? i would like to test my code.
https://www.e-olymp.com/en/problems/1096
Thanks