On the contest dashboard.

Only after the contest.

for 12 backward ropes to be cut are coming from 24,22,...,14. forward ropes to be cut are originating from 5,7,...,11 so total ropes to be cut are 10.

Actually you have misunderstood the problem statement ! By minimal segment it means that i.....j can not be further divided into i...k and k....j

In your eg 1-3 has been turned into 2-2 but 1 and 3 have not been considered. But the problem statement expects CONTINUOUS segments of similar elements with different permutations.

So final answer shoould always be of form 1...k1,k2....k3,k...k,kn.....n.

A more clear problem statement would have helped

First calculate mm[i] for each subset i of 9 cells where mm[i] denotes the number of perfect matching for this subset. This can be calculated via DP/brute-force easily.
then let dp[i][j] denote the height i and topmost floor has subset j matched to i+1 then answer for any N = dp[N][0]. All values can be calculated in O(3^9*N) as follows:

dp[0][0] = 1;
  rep(i, 1, 5002) {
    rep(j, 0, 511) { //previous subset was j.
      int x = 511 ^ j;
      for(int k = x; ; k = (k - 1)&x) {//for a subset k of the remaining
        dp[i][k] += mm[511 ^ (j | k)] * dp[i - 1][j]; dp[i][k] %= mod; //number of matching of whole - j - k
        if(k == 0) break;
      }
    }
  }

I came up with a different approach from sumit16's DP. My DP also has O(N3⁹) complexity and works as follows.

Let f(i, m₁, m₂) be the number of pairings considering floors 1 to i such that floor i's rooms in bitmask m₁ still need to be paired and rooms in bitmask m₂ are currently paired with the floor below, which is i - 1.

Then the answer is f(N, 511, 0): consider floors 1 to N, all 9 rooms in floor N still must be paired and no room in floor i is currently paired with the floor below, which is N - 1.

I'll use set notation for bitmasks when convenient.

Base cases:

$latexbug$

General transition (i ≥ 1, m₁ > 0):

Let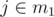 be any unpaired room (the smallest will do fine). Then:

$morelatexbug$

where V(j) denotes the set of neighbour rooms of j which are present in m₁.

You're probably thinking: "this is a 4-state per element bitmask, so it runs in O(N4⁹)!". Yes! But you can supress one of the 4 states. If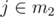 , then j is already paired and cannot also be in m₁. So you can translate a tuple (i, m₁, m₂) to an array indexing [i][x₁][x₂]...[x₉], where x_j = 2 if 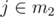, x_j = 1 if 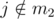and 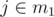, and x_j = 0 otherwise. And you should store 2-byte integers, so MLE won't be a problem.

Similiar DP approach, but (maybe) faster:

dp[layer][level][now_consider]: The first two dimension is the same as the dp mentioned above, while the third dimension is the cell we are considering. For a particular cell, we can either

1. ignore it (and match with the upper level one)

2. pair with the cell on the right

3. pair with the cell on the bottom

(To avoid duplicate, we don't consider pairing with cell on top or left).

The transitions are: if k == the bottom-right cell, we cannot pair it anyway, therefore we consider next level, i.e. (i + 1, j, 1) += (i, j xor 511, k) else, (i, j, k + 1) += (i, j, k)

pair with right: (i, j + bit(k) + bit(k+1), k + 1) += (i, j, k) if k is not the rightmost cells and the bitset in j allows

pair with right: (i, j + bit(k) + bit(k+3), k + 1) += (i, j, k) if k is not the bottommost cells and the bitset in j allows

As the transition is now O(1), the overall complexity is O(N * 2^K * K), where $K$=9 is the number of cells

code: http://codeforces.net/gym/101078/submission/20441012

the normal DP solution works: dp[i] = min time for first i songs:
dp[i] = dp[j]+(sum(j+1..i)>m?(sum(S_j+1..S_i)-m)*a:(m-sum(S_j+1..S_i))*b)

j varies from i-60*m..i by the condition that atleast one second for each song — this will give TLE
j varies from i-2*m..i — AC cause the min point will occur <=2*m.
O(n*m)

make a bipartite graph with H vertices on left, V on right. For each horizontal word i that conflicts with a vertical word j, edge between i-j. Answer = H + V — bipartite_matching(graph) cause min_cut is the minimum number of edges needed to be cut :D

Use a doubly linked list and simulate the operations(list in c++).

In this test case your solution does not give the minimum penalty.

UPvotes to you sir :))

Use scanf and printf :)

Consider mm[1<<9] array which stores the no. of correct pairing possible

mm[0] = 1;

for i=1 to (1<<9)-1 1. Choose a filled room say k ( whose bit is set to 1 in i ) 2. Its pairing will be above/below/left/right 3.mm[i] = mm[i-k-left] + mm[i-k-right] + mm[i-k-up] + mm[i-k-below];

Coming to dp part refer the dp soln in comment : http://codeforces.net/blog/entry/46993?#comment-313759

let dp[i][j] be no. of correct pairings such that floor 1 to i have been filled and set(j) rooms of floor i are to be paired with corresponding set(j) rooms of floor i+1

in the dp soln in comment, i stands for curr floor, j for set of rooms from i-1 floor which have to be paired with curr floor . Also see that the set(j) rooms have to be compulsarilty paired with set(j) rooms of curr floor. From the remaining (x in soln) 511 — set(j) rooms we have two choices : 1. Pair them on the same floor 2. Or else pair them with upper floor.

So k stands for set of rooms to be paired with upper floor. Hence dp[i][k] = dp[i-1][j] * mm[rooms to be paired on curr floor] = dp[i-1][j] * mm[511 — j — k ) since j and k rooms dont pair on curr floor.

Also pairings of curr floor have been calculated in mm. Note that k will always be a subset of 511 — j. Also final ans will be dp[N][0]

see this comment http://codeforces.net/blog/entry/46993?#comment-313836

U misunderstood the problem statement

http://2010.bapc.eu/problems.html

99

Did you try to generate random test cases and use a model solution to check if your solution is printing right answer? It is usually in off, except for border cases.