Can anyone please explain the analysis to problem F? Unfortunately this time the editorial is in japanese.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 155 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/22/2025 23:56:07 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Consider the sequence of cards that will be taken until the end of the game. For example, if n = 5, m = 4, k = 6 then it can look like:
Alice wins if the sequence consists of exactly n a's, no more than m b's and no more than k c's. Let's say there are s b's and c's totally. The rest of cards may be chosen with 3m + k - s ways, and the revealed cards may be chosen with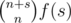 ways where f(s) is the number of strings consisting of s characters a and b in total from which no more than m are a's and no more than k are b's.
ways where f(s) is the number of strings consisting of s characters a and b in total from which no more than m are a's and no more than k are b's.
It's easy to see that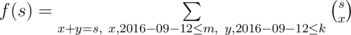
If we draw a Pascal Triangle, this is a section of rectangle (0, 0) — (m, k) with a diagonal line that looks like a segment consisting of binomial coefficients with fixed first argument. There is no closed form for such sum, but it's easy to see thath f(s + 1) is almost equal to 2f(s), you only need to carefully consider O(1) binomial coefficients at the border. So, the solution is: calculate using DP the function f(s + 1) = 2f(s) + [O(1) binomial, 2016 - 09 - 12 coefficients], and then output the answer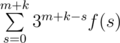 . Binomial coefficients may be calculated in O(1) if we precompute all factorials. Overall complexity is O(n + m + k).
. Binomial coefficients may be calculated in O(1) if we precompute all factorials. Overall complexity is O(n + m + k).
Can someone explain problem E also..
I have not solved the problem but it seems plain dijkstra. The state is: (node, color). Even though there may be many node's and many color's but, number of interesting (node, color) pair is not more than number of edges.
Not Dijkstra but BFS, actually, since all edge lengths are 0/1.
Can you please elaborate the solution a little..
First, find connected components of railway lines. Two railway lines are in the same connected components if they belong to the same company and they are connected through rails of this company.
Then, construct a bipartite graph. The vertices on the left correspond to stations. The vertices on the right correspond to connected components. Add an edge between a left vertex and a right vertex if the station is incident to one of the rails in the connected component.
The solution is (the shortest path in this bipartite graph) / 2.
Can you please explain how finding the shortest path in the constructed bipartite graph would be equivalent to finding shortest path between nodes 1 to n.
All the vertices of the original graph are on the left and components of the edges on the right. Moving from 1 vertex to another (on the left side) passes over two edges in the bipartite graph but is of actual cost 1 in the original graph (hence we divide by 2). Also each such movement (left->right->left) is equivalent to changing the edge-component (or rather changing the company whose edge you are travelling on in the original graph which incurs a cost of 1). This is precisely what you are asked to minimize.