Pathetic_loser's blog

XXI Polish OI problem — Couriers
By Pathetic_loser, 8 years ago, In English

Problem link

The best I came up with is O( N*sqrt(N)*log(N) ) using MO to sort the queries — the log(N) part is for querying the most frequent value in that range. Got TLE with that — even in some smaller cases.

Any hint? :)

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
8 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

I solved this problem using random sampling — I took k random indices (where k is a constant) in the range for each query and checked if the number at that index appeared enough times in the range to be dominating (in O(logn) with a binary search), so the total runtime is m*k*log(n). The probability of failing to find the dominating element of a query is always less than 1/(2^k).

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Could you please explain how to check if a number appeared enough times in the range with a binary search?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +6 Vote: I do not like it

      For each number keep a sorted list of all of the indices where that number occurs. Then, create a function f(L, x) that counts the number of elements in a list L less than a number x. The number of occurrences in the range is f (L, b+1) — f (L, a).

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Great solution :) What did you consider to decide on the value of K?

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it +3 Vote: I do not like it

          I went with 35, but it might be necessary to decrease it depending on the time limit.

          → Reply
»
8 years ago, # |
  Vote: I like it +13 Vote: I do not like it

There's a deterministic solution which runs in O(log n) per query. Think about how you'd solve a single query in linear time, but constant memory. If you fail to do this on your own, look it up, it's a somewhat classical interview problem. You'll notice that it has some neat properties that come in handy for solving multiple queries.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Thanks! That was helpful. I actually read solution long ago about how to do for frequency > N/3 ( linear, constant space ) but totally forgot until you mentioned "classical interview problem".

    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +21 Vote: I do not like it

Consider a range of numbers. Let's remove pairs of unequal numbers (arbitrarily) until all the numbers are the same. (Or there are no numbers left). There will be at most 1 number left. Can any other numbers be dominating in this range?

Now, you can use a segment tree to simulate this process. For each node, store some information about the number remaining after cancelling out unequal numbers.

Here's the code for combine (spoiler!)

→ Reply
»
8 years ago, # |
  Vote: I like it +15 Vote: I do not like it

I solved it like this: Let Length = R — L + 1. Consider the value bit by bit. Suppose we're considering the kth bit. If in [L, R], there're more than (Length / 2) values with kth bit equals to 0, then kth bit of answer must equal to 0, otherwise it's 1, and if there are exactly Length / 2 value 0 and Length / 2 value 1, there won't exist an answer.

After that, check if that answer appears more than (Length / 2) times using whatever you want (I use a vector and binary search).

→ Reply
»
8 years ago, # |
← Rev. 4   Vote: I like it +8 Vote: I do not like it

Another non-deterministic solution in .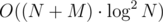

Observe that if some element is dominant in an array, if we split this array into some parts, it must also be dominant in at least one of these parts(this is easily provable by contradiction). Keep a persistent segment tree to find frequency of an element in a sub array. Now, build a segment tree on the dominant value in a subarray. As we know during range query we visit at most nodes, we can query the dominant member of each of these parts in the entire subarray and check for it's dominancy.

Code
→ Reply