Welcome to 2016-2017 CT S03E07: Codeforces Trainings Season 3 Episode 7 - HackerEarth Problems Compilation. The training duration is 5 hours. It is opened for teams as well as for individual participants. After the end you may use the practice mode to complete problem solving. Also it will be available as a virtual contest for whose of you who can't take part today. Please, do not cheat. Only fair play!
Many thanks to Errichto for the preparation of the training. He has saved me!
Visit Codeforces::Gym to find the contest and register.
We are planning to start on October, 26, 2016 13:10 (UTC).
It is possible that the problems will be too easy for some participants, it is possible that we will add some problems.
Good luck!
UPD: The training is over. Many thank to HackerEarth for problems! Undoubtedly Errichto is my hero of the day — he've prepared the training! Special thanks to the problem writers.
The editorial is in the comment http://codeforces.net/blog/entry/47985?#comment-322692
The registration starts 6 hours before the contest!! isn't that a short time to register?
It is open during the whole contest. No need to hurry.
And then they got disqualified for searching problems in the Internet and copying all solutions.
I want to thank HackerEarth for allowing us reusing the problems (also thanks to the setters!), and to thank Mike for carefully checking everything, so you could have a nice contest. You can enjoy amazing and detailed editorials mostly written by pkacprzak.
A — Yet Another Problem with Strings
To solve this problem, we will first note that the stickman has a central edge, i.e. the torso, to which every other edge is connected, and unlike the arms and legs there is no ambiguity about which edge has been used for which torso as there is only one torso.
So if we iterate over every edge of the given graph and count how many times we can use the given edge as a torso and add all those values up, we will get our answer. So lets consider some edge uv (between th vertices u and v), and try and find out how many stickmen can be made with uv as a torso.
The first instinct is to pick some 3 neighbors of u and some 2 neighbors of v. So we multiply the number of ways we can pick 3 neighbors of u with the number of ways we can pick 2 neighbors of v and would add that to our answer. However, that is wrong as there may be some vertices which are neighbors of both u and v and we may end up picking the same vertex twice in one stickman, once as an arm or a head, and once as a leg.
Clearly our previous approach does some overcounting so lets fix that. When we are processing edge uv we will divide the neighbors of u and v into 3 categories:
1) Adjacent to both u and v.
2) Adjacent to just u.
3) Adjacent to just v.
Now, when we are counting number of ways to pick 3 neighbors of u, we will consider the following cases: All of them are from category 2, 2 of them are from category 2 and 1 of them is from category 1, 1 of them is category 2 and 2 are from category 2 and finally when all of them are from category 1. Similarly, we have multiple cases for the 2 neighbors of v we will pick. We will consider all possible pairs of these cases and add the answer for each to our final answer.
The only detail that is left is how to find out the number of ways to pick r vertices from a set of n vertices. This is a fairly common result in combinatorics and is given by: n!/(r! (n-r)!) Refer here for more details : https://en.wikipedia.org/wiki/Combination
D — Strange Queries
E — Bravebeart
F — GukiZ Height
H — Precise Shopping
You can see my codes for H (both should get AC but the latter one is faster):
-
From a number 'x' greater than 2 you can't go to any numbers other than 2, x-2 and x+2 (proof: the distance to other numbers is even, so it can't be prime). From this fact you can prove that any optimal path between some 'a' and 'b' uses only vertices 2, a-2, a, a+2, b-2, b, b+2. If you want to prove it, use the fact that after moving to some number other than those seven, we will shortly have to get back to a number 2. It's important here that (except for a triple 3, 5, 7) the three consecutive odd numbers numbers y, y+2, y+4 can't be all primes.
For each of those seven numbers you must check if it's prime and for each pair you must check if its difference is prime. Then you should run BFS. It can be proved that there exists at most one optimal way so the answer "Poor Benny" never happens, but it doesn't affect the implementation much.
J — Valentina and the Gift Tree
K — The World of Trains
And congratulations to danilka.pro, HellKitsune and IlyaLos for winning the contest (after they were far behind in the first half of the contest). Nice job!
Time limit for problem A is very generous. It alows solution with complexity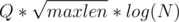
to pass.
It was intended. What wasn't intended is that O(N·Q) passed, what was the combined results of: not all solutions uploaded in Polygon, weak tests and the fact that I wanted to let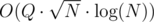
to pass, even though we didn't let it pass in the original contest a year ago, what I didn't remember (and unfortunately I marked this solution as AC in Polygon a year ago). If I knew that some O(Q·N) passes, I would cut TL significantly.
Could you please answer me a question?
I've thought up an idea that when adding a char after one of S , form a line just like a tail,and when the total length of the tails meets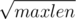
, rebuild the A.C Auto and its fail tree.
I'd like to know whether it's right or what yours is.
Thx.
Thank you! Somewhy we were mostly stuck on problems solved by significant amount of teams, wondering what are we missing, and came up with them only closer to the end of the contest.
As about problem A, one of our state teams got AC with Aho-Corasick algorithm (offline!). We checked their solution and found that it's very unlikely to be true, so it seems that tests are not weak just about missed TLEs.
Though maybe you can show us why it works, or maybe it can be modified to be online? We've found some other solutions with Aho-Corasick algo, but none of those were fine to us.
I've got something puzzling about question A.
I'd like to ask how it works to modify the fail tree of Aho-Corasick Auto when adding a new node after one of S.
Or the solution doesn't depend on A.C Auto at all？
But how to "know how many strings from S are prefixes of the string corresponding to this node"?(Please ignore the question above)
And how to operate when it's necessary that "Next, if there is no node corresponding to Si with appended c, we create it and set up its counter"?
I've the same question how to modify fail tree efficiently?? I tried one pass on all nodes with level one less than level of newly added character but got TLE.
In A's solution: "contains(t) := returns YES if at least one string from S is a prefix of string t. Otherwise returns NO". I though it was substring instead of prefix?
Exactly, thx
I was trying to understand what other teams did with problem A and I found a problem: you don't have tests with equal strings. I changed multiset to set and still got AC. If you have two equal strings (with equal hashes) and change one of them you somehow delete both of the hashes from the set and it should get WA. :(
Any Help with Problem A
Nice contest, and thanks for the fast editorial!
Also J was such a HLD bait in my opinion, hahah
"HLD is Heavy — Light Decomposition. Alot of code."
How to solve G?
I used inclusion exclusion.
Say we have m numbers out of which we have to choose n numbers with repetition allowed, without any constraint, the number of ways is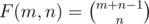
.
Let x = P1P2... Pk, where Pi = piei, where ei is exponent of p in x.
Since x divides lcm(a1, a2, ... an), each of Pi divide at least one of ai. Let us remove cases where some of Pi divide no ai.
So lets choose a subset Q = {Q1, Q2, ...Qm} of P = {P1, P2, ... Pk}. Let num(Q, a, b) denote the number of integers lying in [a, b], not divisible by any of Qi. Note that num(Q) can be found in O(m * 2m) by inclusion exclusion again.
The answer is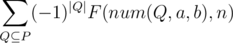
Since we are considering subsets of subsets, the overall complexity is O(k3k + n2k)
Can Anyone please DM me the code of Problem-D