Tutorial is loading...
Setter's code
int n, a, b;
string s;
cin >> n >> a >> b >> s;
a--, b--;
cout << ((s[a] - '0') ^ (s[b] - '0'));
Tutorial is loading...
Setter's code
int go(ll l, ll r, ll need, int alphSize)
{
ll m = l + (r - l) / 2LL;
if (need < m)
return go(l, m - 1, need, alphSize - 1);
else if (need > m)
return go(m + 1, r, need, alphSize - 1);
else
return alphSize;
}
void solveABig()
{
int n;
ll k;
cin >> n >> k;
ll sz = 1;
for (int i = 1; i < n; i++)
sz = sz * 2LL + 1LL;
cout << go(1, sz, k, n);
}
Tutorial is loading...
Setter's code
int n;
cin >> n;
if (n == 1)
cout << -1 << endl;
else
cout << n << ' ' << n + 1 << ' ' << n * (n + 1) << endl;
Tutorial is loading...
Setter's code
int a[maxn];
vector<int> g[maxn];
ll sum_subTree[maxn], mx_subTree[maxn];
void dfs1(int v, int p) {
sum_subTree[v] = a[v];
mx_subTree[v] = -llinf;
for (int i = 0; i < g[v].size(); i++) {
int to = g[v][i];
if (to == p)
continue;
dfs1(to, v);
sum_subTree[v] += sum_subTree[to];
mx_subTree[v] = max(mx_subTree[v], mx_subTree[to]);
}
mx_subTree[v] = max(mx_subTree[v], sum_subTree[v]);
}
ll ans = -llinf;
void dfs2(int v, int p, ll out) {
if (out != -llinf)
ans = max(ans, sum_subTree[v] + out);
vector<pair<ll, int> > miniset;
for (int i = 0; i < g[v].size(); i++) {
int to = g[v][i];
if (to == p)
continue;
miniset.pb(mp(mx_subTree[to], to));
sort(miniset.rbegin(), miniset.rend());
if (miniset.size() == 3)
miniset.pop_back();
}
miniset.pb(mp(-llinf, -1));
for (int i = 0; i < g[v].size(); i++) {
int to = g[v][i];
if (to == p)
continue;
ll cur = miniset[0].s == to ? miniset[1].f : miniset[0].f;
dfs2(to, v, max(out, cur));
}
}
int main() {
for (int i = 0; i + 1 < n; i++) {
int u, v;
read(u, v);
u--, v--;
g[u].pb(v);
g[v].pb(u);
}
dfs1(0, -1);
dfs2(0, -1, -llinf);
cout << ((ans == -llinf) ? ("Impossible") : to_string(ans));
return 0;
}
Tutorial is loading...
Setter's code
int can(int len) {
for (int i = 0; i < 8; i++)
cur[i] = 0;
for (int i = 0; i <= n; i++)
for (int j = 0; j < (1 << 8); j++)
dp[i][j] = -inf;
dp[0][0] = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < (1 << 8); j++) {
if (dp[i][j] == -inf)
continue;
for (int k = 0; k < 8; k++) {
if (j & (1 << k))
continue;
int it = cur[k] + len - 1;
if (it >= in[k].size())
continue;
amax(dp[in[k][it] + 1][j | (1 << k)], dp[i][j]);
it++;
if (it >= in[k].size())
continue;
amax(dp[in[k][it] + 1][j | (1 << k)], dp[i][j] + 1);
}
}
cur[a[i]]++;
}
int ans = -inf;
for (int i = 0; i <= n; i++)
ans = max(ans, dp[i][(1 << 8) - 1]);
if (ans == -inf)
return -1;
return ans * (len + 1) + (8 - ans) * len;
}
int main() {
for (int i = 0; i < n; i++) {
in[a[i]].push_back(i);
}
int l = 1, r = n / 8;
while (r - l > 1) {
int m = (l + r) >> 1;
if (can(m) != -1)
l = m;
else
r = m;
}
int ans = max(can(l), can(r));
if (ans == -1) {
ans = 0;
for (int i = 0; i < 8; i++)
if (!in[i].empty())
ans++;
}
cout << ans;
return 0;
}











Could anyone explain D to me again? I could not fully get the editorial.
Do DFS.. For each child get 2 values their pleasentness sum and the max pleasentness and 2nd max pleasentness value till that child.
Keep one max_ans and update it with max(max_ans,max1+max2)
Update and return your sum and max(your sum, max)
Do the above for each node and finally print max_ans
This works because of the 'max1' and 'max2' coming from the different subtrees of the children thus satisfying our condition that the subtrees shouldn't intersect
If we run DFS from every node, then it wouldn't be O(N) already right?
No you don't have to run dfs from every node. It is mentioned in problem that 1 is the root ie the whole tree hangs on node 1 so just run dfs from node 1
My solution to B is, the answer is the index of the right most bit 1 (1-based) in the k. 22954844
I got this by solving some random values of n and k, but have no proof why this is correct :D, anyone knows why?!
If it holds for n, then it also holds for n+1. Proven. Ps: Isn't is the most 0 on the right? (In base 2)
https://oeis.org/A001511
Not sure this is an answer. Just another relevant observation while talking about all things binary :P But the answer can be obtained by binary-searching the index k in the range [1,2^n — 1] and decrementing the answer variable by 1 at each "step".(answer is initially n). We see an obvious analogue coz for any n, the value n is at the "mid" of the sequence. Formally, the answer somehow depends on the number of comparisons a binary search would do, in order to hit index k in the range [1,2^n — 1] See submission for clarity 22961954
I did this with some beautiful observation, just three lines of code. check 22968081
Check my solution to 22967686
beautiful indeed!
Woah, that's pretty awesome! How did this solution strike you? What was your initial thought? I find that such solutions are really unintuitive :/
For me, I realized it in this way:
Tried to obtain the first occurrence of k -> Realized it is related to 2^x -> noticed that they appears on a fixed interval -> try for some more corner cases -> code it
One line solution to B — 22997490
what this does ?
It uses a builtin function of the GCC compiler to calculate the position from the right of the first non-zero (1) bit in the binary representation of k.
If you look at the way the sequence is generated , you'll find that this is equal to the number at k.
This is much more efficient than implementing the algorithm on your own.
Built-in Functions Provided by GCC
In particular, I think clz / clzll is the must learn one as it is very useful in handling bitmasks.
As a guy who doesn't memorize a lot of commands, I used clz(x & -x) for this task instead.
— Built-in Function: int __builtin_ffs (unsigned int x) Returns one plus the index of the least significant 1-bit of x, or if x is zero, returns zero.
I have a bit different approach for problem E, which fits in the TL even when N is up to 10^6.
The solution consists of tho phases. The problem is much easier if we can find such K that every element will be present either K or K+1 times. We can binary search to find it. Foreach step of step binary search, we will define dp[mask] as the smallest index of the sequence for which it is possible to have a sequence of number from mask ending on it. Updating this dp is quite easy, we just check all possible additions of the last element to our mask and binary searching on prefix sums the new interval.
The second phase is as follows: we have the correct K found, so every number will be present either K or K + 1 times. Once again we will do bitmask dp, just considering all possible 28 cases this time and using the previous idea.
Overall complexity: O(2K * K * logN * logN + 22K * K * logN)
You can refer to my submission: 22976778
isn't it just binary search on possible values of len?
Good idea. I'd just like to add some improvement.
Define dp[ind][mask] as the size of largest sequence that can be built starting from index ind and only using elements unset in mask, with each element being repeated x or x + 1 times.
For each state, either you'll add the element at index ind for x times, or x + 1 times, or 0 times and move to ind + 1.
We can do some pre-computation to be able to get the position of x - th following occurrence of some element in O(1).
Clearly, this function for a fixed x is O(N * 2K).
As you've said, we can do binary search on x, and the validation function will be whether this dp returns 0 or not.
This way achieves better complexity and simpler code.
Total complexity: O(log(N) * N * 2k).
Sir I did not understand the binary search part how are u using binary search and for what purpose? I am a newbie it would be very helpful if you guide ?
Each number in the required sequence will be repeated x or x + 1 times.
If there's a sequence with some x, then of course there's another sequence with x - 1. You can just delete one occurrence of each number from the first sequence to get the second one.
Since you want to maximize the sequence length, you want to maximize x. And since the possibility of getting sequence with x is monotonic (i.e. it's true in some range [0, y) , and false in [y, OO) ), you can use binary search to get y.
can someone explain to me how did we get those formulas for C?
2/n = 1/n + 1/n
so, x = n; observe that, 1/y + 1/xy = 1/x if y = x+1;
2/n = 1/n + 1/n
So we have just made the problem much easier because how we just need to represent 1/n as a sum of 1/x and 1/y (then we would have 2/n = 1/n + 1/x + 1/y)
Then let's take a look at the second testcase and find out that x = n + 1 and y = n * (n + 1) are right for all the cases (just because 1/(n + 1) + 1/n(n+1) = n + 1 / n(n + 1) = 1/n)
Let's check that 1/x != 1/y != 1/z
n != n + 1 for every n
let n = n^2 + n then n^2 = 0, n = 0. But all n are positive so this also work for every n and the last case n + 1 = n^2 + n <=> n^2 = 1 <=>(n is positive) n = 1. So in this case we can't represent 2/n as 1/x + 1/y + 1/z
Finally x, y, z would be less than 1e9 because n less than 1e4, so n^2 + n is less than 1e8 + 1e4 , so this restriction is useless.
As for me, I can't guess why this problem costs only 1250, I think it is much harder than B and than common Div2C
Here You can read here for more information :D. This is the website that I googled during the contest time.
Why would someone use google during a competition?
Well. I couldn't figure it out myself. I'm not blue like you :(. But are there any rules about google ? — If there are, I won't do it next time. !
You CAN use the internet , as long as you don't copy-paste somebody else's code. It's perfectly within the rules of the contest. Also , you can consult any book , notes or code that you have personally written beforehand.
See rules: Can-do's and Can't-do's : Point no. 3
I don't know why these other people are downvoting you .. they seem to be under the impression that this is somehow unethical.
I think it's not a good way to improve your skills because you are not actually thinking about the problem. I think rounds should be the place where you try hard to solve the problems by your own. Anyway, that's just my opinion. Good luck!
How could i get the formula for C Mathematically ?
You know sample test 2? Take it for instance... Suppose you can write x=n, y=b, z=(n*b), ok? Then,
2/n = (1/n) + (1/b) + (1/(n*b))
1/n = (1/b) + (1/(n*b))
1/n = (n+1)/(n*b)
1 = (n+1)/b
b = n+1
Then, x=n, y=b=n+1, z= n*(n+1) solve the equation, since they are all different;
For n=1, you can see that there's no solution: if x=1, then we have to find y and z that satisfies 1=(1/y)+(1/z) Since they must be different from x, we can maximize the value of the equation by y=z=2, then we would have a solution; in that case, y=z, and it can't be a solution by the hypothesis that they are all different ;)
As you can see by sample test 1, it is not a "formula", there are other solutions. You have to find a "pattern" that works for any given n ;)
ok i got it .so do u think in it like that or u brute forced and got the formula
I thought like, "if we get x=n, then it's half the way done it. How can I get y and z that satisfies it?", then did some tests with n=2, 3, and then formalized it so that I would be convinced and could start coding it xD
what i did was to break 2/n = 1/n + 1/n now we break the whole equation into 1/n + 1/n = 1/x + 1/y + 1/z now break it further that is
1/n = 1/x + 1/y -> 1
1/n = 1/z -> 2
from 2nd z = n
1/n = 1/x + 1/y ( Diophantine Equation )
whose solutions are x = n + a and y = n + b and a*b = n*n
take a = 1 and b = n
therefore x = n + 1 and y = n + n*n
For B just do F(k)=1 if k is odd, otherwise F(k)=F(k/2)+1, this will be O(logK).
How could we get the formula ?
You can observe it after writing it down, for example with n=4, the positions of:
1: 1, 3, 5, 7,...
2: 2, 6, 10, 14,...
3: 4, 12,...
4: 8
Now you should get the formula.
Question B has been tagged as bitmasks but what i did was something different. here is what i did . http://codeforces.net/submissions/logicbomb1#
How to do it using bitmasks?
You seem to be iteratively checking the remainder after dividing by powers of two.
Instead of that , you can simply check the binary representation of k , and find the first position from the right which is 1.
Like this: 22997490
I thought that problem A was a SSSP problem. After reading the tutorial, I realised that it is indeed a trick. But what if we have 3, 4, 5... companies rather than 2? Are we able to use any simpler algorithm than dijkstra's?
First, observe that we only need edges between adjacent airports (cost 1) and between airports of the same color (cost 0). Although we have the option to jump from any airport to any other with cost |i-j|, we can reach it with the same cost by jumping there 1 by 1 (ex. instead of jumping straight from 3 to 6 with cost |3-6|=3, we can jump 3-4, 4-5, 5-6 with cost 1+1+1=3). So now we would have n edges except that we still have edges with weight zero between every pair of airports with the same color, giving potentially n^2 edges. To fix this, change your nodes from airports to airport colors (since any two airports of the same color can be reached with cost 0, we can consider them the same node). Now you only need the linear edges between adjacent airport (color)s, and you can do a BFS (all edges left are weight 1) with O(n) nodes and edges, so O(V+E) -> O(n)
Note that in the case where there are only two colors, the graph you create will end up being either two connected nodes (if you have both 1's and 0's) or a single node (if the whole string is 0's or all 1's). This means the shortest path will always be 0 if you are the same color as the target, or 1 if you differ.
I found the problem statement of Div-2 D quite confusing. For the pretest-4
Pretest-4-image
Ans according to me should be 19 but ans is 6. Can someone please help me understand why we can't rope between ( 1 and 8 ) and then give 1 to second person ( 16 + 3 = 19 )
In the problem statement : "...the sum of pleasantness of all the gifts that they will take after cutting the ropes is as large as possible."
Because they both have to cut the rope, they can't take the subtree with root = 1.
ok then also lets cut the rope between ( 8 and 10 ) and then between ( 1 and 8 ). Then A will get ( 4 + 3 + 2 + 2 -4 + 3 + 3 = 13 ) and ( 3 ) therefore sum = 16 and not 6. Please correct me if i am wrong
@saisumit : you cant cut the tree that way.
Read the problem statement carefully:
" they will choose prizes at the same time "
[ You can't cut one part, and choose the next part later ]
Also : " they decided to choose two different gifts so that the sets of the gifts that hang on them with a sequence of ropes and another gifts don't intersect "
Remember "they will choose prizes at the same time", so you can't cut the rope between 8 and 10. In another word for "at the same time", you have to choose two disjoint subtrees. So the best solution is choosing only vertex 6 and vertex 7 which has answer = 3.
Could someone plz clearly explain the problem statement of D, do we have to consider different subtrees i.e. can't we take a subtree and then take a subtree which consists of it's ancestor. For eg : — if input is like this
3
2 2 2
1 2
1 3
can we first take 3 and then the remaining subtree of size 2 so total answer is 6, or should we take only nodes 2 and 3. can't we choose two subtrees so that one of them contains the lowest ancestor of other.
You have to pick 2 different subtrees A and B such that there is no common vertex between A and B.
For given constraints in E, I didn't use Binary Search and got AC.
The complexity seems to be O(n2.2k), but I wonder whether all dp states would be useful here or not because the running time seems to be pretty fast even without binary search.
Can someone please explain me what is wrong with my solution for A. I have used the proper way to solve it which should be aaplicable even if two diffrent airports of type a and b were not adjacent to the destination airport.
you just finding min distance with signs similar to s[a] and s[b], but it is not true. example: 5 2 5 11100 here your answer is 2, but you can go to 3rd airport for free (it's similar to s[a]) and you go to s[4] it will cost 1 and you will go to s[b] for free(s[4] equal to s[b])
shortly, answer will be one if s[b] and s[a] different airports, and 0 if they are same
Nice edition
Can someone explain me the 743D — Chloe and pleasant prizes problem statement ???
My solution for problem B 22969930 :D
nice :D
My solution for E is like O(8 * N + 8! * 2^8 * 8 * Log(N)). Did i win an asymptotic war?
And it works for 8 seconds on my local machine with n = 10^7
I didn't came up with a way to maintain the length of dp array so I also ended up trying all possibilities, thank god k! (k=8) isn't that big.
Haven't seen a Div2E problem been this open-ended for a while.
My solution
Time complexity, where k is the variety of cards: O(log^2(N) * k! * C(k, k/2))
Deleted
Isn't the complexity for problem A, O(1) ? Why is it mentioned as O(n) ?
Reading the input is O(n)
Forgive me if I'm being a little amateur here, but is reading a string of length n considered as O(n) or O(1)? We simply do a cin>>str , why would it be considered as O(n) ?
It can't magically read all the characters at once, it takes O(n) to read n characters.
Thank you for the clarification @tfg :)
My one-line solution to B : 22997490
It gives the position from the right of the first non-zero (1) bit. Using a builtin G++ function (that directly uses architecture-level instructions) to do this , is much more efficient.
WOW! This is the coolest thing I came across on the internet today! Didn't even know about builtin functions, but now I do! Thanks :)
How can the complexity of A be O(n) ?
Shouldn't it be O(1)?
Please read the other comments first.This one , in particular.
Sorry about that
Thank you :)
I think test 27 is wrong here. The test case is the following- 10 5 8 1000001110 The jury's answer is 1. It should be two. According to me there are three possible cheapest ways to get to the destination. first is 5 to 6 then 6 to 8 price (8-6 =2) second is 5 to 7 then 7 to 8 price (7-5 =2) third is 5 to 10 then 10 to 8 price (10-8=2) my submission
Answer is 1. Go from 5 to 6. : Costs 0
then 6 to 7 : Costs 1
then 7 to 8 : Costs 0
Total Cost : 1
No need to go directly from 6 to 8, use the fact properly that going from one index a to other index b such that I is 0. Infact, the answer can never be greater than 1 since the indices of transition from a '0' to '1' in the string are always consecutive.
Code
sizeof(A's code) + sizeof(B's code) + sizeof(C's code) < sizeof(D's code)
Could you explain why the bitwise XOR works in problem A? I used a different logic though.
1^1=0 0^0=0 0^1=1
Yes. But first we need to reach the nearest airport of the same company which is at a minimum distance to that of the other company; this minimum distance is the cost. But if only the company numbers 1s and 0s are XORed you'd always get either a one or a zero. But for that to be true, the cost must always be either 0 or 1.
In that case I think it's possibly because 1. You never need more than two moves 2. The free ticket thing (which is I guess the bigger reason for this being true), am I right?
But my naive solution from the contest used three times less memory than the XOR based approach, I don't know why.
There have to be two airports near each other from different companies. You can reach one of them with cost 0,next with cost 1 and the last that you need with cost 0. 0+1+0=1 that's all) And sorry for my bad English:)
Thank You, got it. Could you suggest a few tutorials for Graphs?
I would like to find it too
Can someone please explain me the sample code 3 of problem E. (i didn't got the condition 2 satisfied for it.... as far as the condition is exampled in question 1122 and not 1221)... please.
Conditions doesnt have to be satisfied in the original sequence, your task is to find the maximal subsequence, where they are satisfied.
https://en.wikipedia.org/wiki/Subsequence
Div 2D :- Can someone tell why this got AC D-AC but this didn't D-WA ? Although both of them do same thing ,ie find top two child values. Changes are only in dfs function.
Got it. Thanks :D
can anyone tell me why my code is not working on test case 15.: 23014828 code link:(http://codeforces.net/contest/743/submission/23014828)
I was wrong at the test 15 too. Have you known the reason for that? If you know , please tell me ,thanks?
Problem E is interesting, thanks!
http://codeforces.net/blog/entry/49049?#comment-330919
In setter's code, I can't understand ~~~~~ amax(dp[in[k][it] + 1][j | (1 << k)], dp[i][j]); ~~~~~ mean ? Could anyone explain E to me again? I could not fully get the editorial
amax is a funcion, that is trying to maximize some value. Extremely sorry for using this code-style in a solution written for public.
In E, I did not get the state represented by the dp. What exactly is the mask representing ? I found the editorial explanation insufficient.
Our subsequence looks like this:
c_1, c_1, c_1, c_1, ..., c_2, c_2, c_2, c_2, ... c_8, c_8, c_8, c_8,
where c is some permutation, the order in which we are taking the colors. On each position in the array we have to know how many and what exact colors we had already taken. mask would be a bitmask of 8 bits, where i-th bit is 1, if we had already passed the segment with number i in c, otherwise 0. So the whole state is pos, mask — the maximal length of the subsequence, if we stand at the position pos in the array and already passed all the 1 bits in mask.
Thanks. That helped me get AC.
D approach:
For a node i let ai be its pleasantness.
Let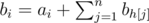 where {h1, h2, ..., hn} are the children of i
where {h1, h2, ..., hn} are the children of i
and let ci = max(bi, bh[1], bh[2], ..., bh[n])
We compute each node bi and ci with a o(n) recursive dfs.
Now we'll find the solution of the sub-graph that contains a node (any) i as root. Denote this procedure dfs(i)
Case 1: the node i is the only node of the graph. Then it is impossible to generate a pair (that is the solution)
Case 2: the node i has only one child. Then the solution will be dfs(h1)
Proof: we can't choose i, in the case we do: we select the root => we can't select another node => we can't make a pair. So we need to choose another node, the solution will be inside the sub graph of the only child. dfs(i) will contain the same pair solution (if it exist) that i should hold
Case 3: the node i has two or more children. Now things get more interesting
Let max1, max2 be the child with 1st and 2nd greater ci respectively. They will always exist as there are two or more children.
now, we need a key observation
Proof: any solution that do so can replace one of its two elements with a node inside sub-graph max1 that will be always greater or equal that any node outside max1
So there are two chances
in the case (1) we will set the solution as cmax1 + cmax2 The sum of the two greater nodes of max1 and max2.
in the case (2) we cant set the solution as cmax1 because the two nodes lie inside max1. So we compute dfs(max1).
As we can do any of the two cases, then we compute both and we return the max value of them. (of course if dfs(max1) has no solution then we use only the case (1))
Total complexity: O(n)
look at my code i m not getting the error http://codeforces.net/contest/743/submission/23025516
The result is the selection of the ci of two nodes, But ci of each node references to bi of some node (the greater in the sub-graph)
And bi is the sum of up to n ai values.
n < = 109
ai < = 109
then bi < = 109 * 109 = 1018
change 'int' with 'long long' :) 23047937
does anyone has a mathematically clear prove for the C problem cause i can't find any online.
My solution for B http://codeforces.net/contest/743/submission/22967882 :DD
What is the way to search for solutions to C, if you couldn't come up with the brilliant factorisation ?
https://codeforces.net/contest/743/submission/86323255 A simple way of doing b is to simply count the power of 2 in k and print it by incrementing one ... eg — for 18 = 2^1 * 3^2 .. ans is 2 do have a look at the solution.
Wow! how did you observe it and guess it?
Just tried relating the position with the sequence
if anyone has solved 2nd que using recursion,give ans link in comment section.
I just bruteforced C. Couldn't come up with that factorization. Here's what I did:
We are given n. The equation is 2/n = 1/x + 1/y + 1/z
let p = lcm(2,n). Actually we need to find a common multiple of 2 and n. But for now let's just find lcm(2,n) because any common multiple of 2 and n is also a multiple of lcm(2,n).
(2*p)/(n*p) = 1/x + 1/y + 1/z = (a + b + c)/lcm(x,y,z)
Now we need to find a p or common multiple of 2 and n such that the equation below satisfies.
I bruteforced to find all the common multiple of 2 and n and then get all it's factors in a vector. Then, I ran 3 loops to find a,b and c where above equation satisfies.
here's my code