snarknews's blog

SnarkNews New Year Contests — 2017
By snarknews, history, 8 years ago, translation, In English

Traditionally, SnarkNews runs two New Year Contests.

The New Year Blitz Contest (Multiple Language Round) will start at 16:00 31.12.2016 and ends at 08:00 01.01.2017 Moscow Time. Contest consists of 13 problems. Some of those problems are based on problems, used at official or training contests in 2016. Contest rules are based on the ACM system with two important modifications.

  1. Penalty time is calculated as distance between time of first successful submit for the contestant on this problem and 0:00:00 01.01.2017, i.e. successful submissions at 23:50:00 31.12.2016 and at 0:10:00 01.01.2017 will both have penalty time 10 minutes (600 seconds).

  2. Multiple Language Round rule: If for the first successful submit for the contestant on the some problem was used the programming language, which was never used by this contestant in his previous first successful submits on other problems, contestant receives language bonus: his summary penalty time is decreased by 100 minutes (6000 seconds). Note that different implementations of the same language are counting as same language, i.e. Java 6 and Java 7 are both counted as Java, C++ 32 bit and C++11 64 bit both as C++. Additionally, C and C++ are counted as same programming language.

Contest will be running on Yandex.Contest system. Link for registration and participation.

13'th Prime New Year Contest will start at 0:00 30.12.2016 and finish at 23:59 10.01.2017 Moscow time. Traditionally, Prime New Year Contest consists of problems, which were presented at team programming contests in 2016 and never solved on the contest. For the Prime New Year contest plain ACM rules are used.

Idea of Prime Contest was first implemented by Andrey Lopatin and Nick Dourov at Summer Petrozavodsk training camp at 2003; in Russian word "Prostoj" used in meanings "prime" and "easy", so, contest was called "Prostoj contest" but was composed of extremelly hard problems, numbered with prime numbers (2,3,5 etc). Since then such a numeration is traditionally used for contests, consisting of very hard problems only.

Contest will be running on Yandex.Contest system. Link for registration and participation.

Both contests have English statements. Registration is open till the end of the contest.

  • Vote: I like it
  • +124
  • Vote: I do not like it

Comments Comments (5)
| Write comment?
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Is there an editorial for the New Year Blitz contest?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    How to solve G? I can share my solutions for the rest.

    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +15 Vote: I do not like it

How to solve 3. (Ancient City) and 17. (Generator)? Maybe there are some online editorials in English?

I hope Ancient City's intended solution doesn't require coding dynamic convex hull. I thought about decomposing interval of time when points lives into base intervals, compute hulls in every base interval and then for each query binary search on angle of side which line intersects, but htat leads to O(log3n) per query which I guess is too slow (one log for binary search on sides's slope, one for log n base intervals, one for binary search on extremal points with respect to chosen slopes). Aaaand exactly during writing that I realized that last log is not necessary since it can be reduced if we do parallel binary search and process all queries of maximal points wrt some slopes from one binary search pass in linear time of convex hull size <_<. However it is still messy to code.

So, what about 17? I thought for a long while and maybe I have a solution giving correct answers, but significantly too slow (but better than some straightforward Gausses :P). Summon zimpha, aid.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +35 Vote: I do not like it

    First, let's solve this problem for n = 1. Let s be our string, p(i) be probability that there are no occurrences of s in the first i symbols produced by generator, q(i) be probability that there is exactly one occurrence of s in the first i symbols and it ends at i-th symbol. Also, let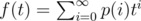 , and .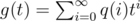

    Assume that we generated i symbols and didn't find s. When we generate the next symbol, we either don't find s or find one occurrence of it, and in the latter case it ends at (i + 1)-th symbol. So, p(i) = p(i + 1) + q(i + 1), and tf(t) = f(t) + g(t) - p(0) - q(0) = f(t) + g(t) - 1.

    Now, instead of appending 1 symbol, let's append the whole s. Then, we can find the first occurrence of s at positions i + 1, i + 2, ..., i + |s|, but not all of them are possible. If we find s at position i + j, then s must have a border of length j, and all such j are good. Let B be the set of all such j. So, we have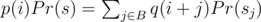 , where 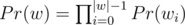, and sj is j-th suffix of s. And in terms of generating functions: 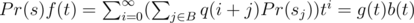, where .

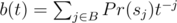    So, we have system of 2 linear equations, which we can solve to find f(t) for any t. The answer to our problem, is, of course, f(1).

    We can do the same thing with multiple strings, instead of 2 equations with 2 variables, there will be n + 1 equation with n + 1 variable. But in this case f(1) will be the expected time to find occurrence of some string from our set, and we need to find all strings from our set. We can do it using inclusion-exclusion formula. 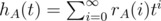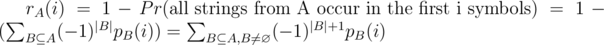Let pA(i) be probability that no string from the set A occurs in the first i symbols produced by the generator, rA(i) be probability that not all strings from A occur in the first i symbols, , and . , and 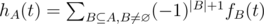. So, we can find hA(1) by counting fB(1) for all . The complexity is O(n2l + 2nn3).

    There is a small problem with this solution. When we use Gauss, we can get a matrix with determinant divisible by 109 + 7, and we will not be able to solve the system. I solved this problem by not doing anything and hoping that there are no such tests, which turned out to be true.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    For Ancient City, there is a similar problem Dogs' Candies in ACM/ICPC 2014 Guangzhou and another similar problem Misha & Geometry in CodeChef June Challenge 2016.

    Divide the convex hull into Upper Convex Hull and Down Convex Hull. It's ok just to consider Upper Convex Hull (Down Convex Hull is just the same).

    For each point (xi, yi), find the interval of time [li, ri) when the point exists. Now we can solving all problem use divide-and-conquer by queries. The pseudo code is below:

    def solve(L, R, queries):
  M = (L + R) >> 1
  for q in queries:
    if q.l <= L and q.r >= R:
      upper_hull.add(q.x, q.y)
    elif q.l >= R or q.r <= L:
      continue
    else:
      new_queries.add(q)
   if L + 1 == R:
     # here, we got the upper convex hull at time L
   solve(L, M, new_queries)
   solve(M, R, new_queries)

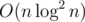    You can use a persistent treap (or treap with rollback) to maintain the upper/lower convex hull (Since we only need to insert point to treap, this is easy to code). Then, adding point in upper convex hull will work in , solve(0, n) function has complexity , so the total complexity is .

    As for the geometry part, several simple binary search will work.

    → Reply