How to solve G? I can share my solutions for the rest.

First, let's solve this problem for n = 1. Let s be our string, p(i) be probability that there are no occurrences of s in the first i symbols produced by generator, q(i) be probability that there is exactly one occurrence of s in the first i symbols and it ends at i-th symbol. Also, let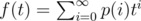 , and .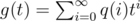

Assume that we generated i symbols and didn't find s. When we generate the next symbol, we either don't find s or find one occurrence of it, and in the latter case it ends at (i + 1)-th symbol. So, p(i) = p(i + 1) + q(i + 1), and tf(t) = f(t) + g(t) - p(0) - q(0) = f(t) + g(t) - 1.

Now, instead of appending 1 symbol, let's append the whole s. Then, we can find the first occurrence of s at positions i + 1, i + 2, ..., i + |s|, but not all of them are possible. If we find s at position i + j, then s must have a border of length j, and all such j are good. Let B be the set of all such j. So, we have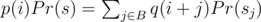 , where 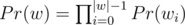, and s_j is j-th suffix of s. And in terms of generating functions: 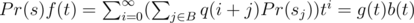, where .

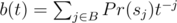So, we have system of 2 linear equations, which we can solve to find f(t) for any t. The answer to our problem, is, of course, f(1).

We can do the same thing with multiple strings, instead of 2 equations with 2 variables, there will be n + 1 equation with n + 1 variable. But in this case f(1) will be the expected time to find occurrence of some string from our set, and we need to find all strings from our set. We can do it using inclusion-exclusion formula. 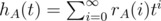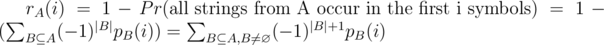Let p_A(i) be probability that no string from the set A occurs in the first i symbols produced by the generator, r_A(i) be probability that not all strings from A occur in the first i symbols, , and . , and 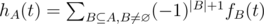. So, we can find h_A(1) by counting f_B(1) for all . The complexity is O(n²l + 2ⁿn³).

There is a small problem with this solution. When we use Gauss, we can get a matrix with determinant divisible by 10⁹ + 7, and we will not be able to solve the system. I solved this problem by not doing anything and hoping that there are no such tests, which turned out to be true.

For Ancient City, there is a similar problem Dogs' Candies in ACM/ICPC 2014 Guangzhou and another similar problem Misha & Geometry in CodeChef June Challenge 2016.

Divide the convex hull into Upper Convex Hull and Down Convex Hull. It's ok just to consider Upper Convex Hull (Down Convex Hull is just the same).

For each point (x_i, y_i), find the interval of time [l_i, r_i) when the point exists. Now we can solving all problem use divide-and-conquer by queries. The pseudo code is below:

def solve(L, R, queries):
  M = (L + R) >> 1
  for q in queries:
    if q.l <= L and q.r >= R:
      upper_hull.add(q.x, q.y)
    elif q.l >= R or q.r <= L:
      continue
    else:
      new_queries.add(q)
   if L + 1 == R:
     # here, we got the upper convex hull at time L
   solve(L, M, new_queries)
   solve(M, R, new_queries)

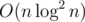You can use a persistent treap (or treap with rollback) to maintain the upper/lower convex hull (Since we only need to insert point to treap, this is easy to code). Then, adding point in upper convex hull will work in , solve(0, n) function has complexity , so the total complexity is .

As for the geometry part, several simple binary search will work.