Shafaet's blog

HackerRank HourRank 16
By Shafaet, history, 8 years ago, In English

Start your new year with Hourrank 16 on 2nd January, 2017. You have just 1 hour to solve 3 algorithmic problems.

The chief author of the round is svanidz1. Thanks to danilka.pro, malcolm for testing. And finally thanks to Wild_Hamster for helping to finalize the problems and dataset.

If two person has the same score, the one who reached the score first will win. There are subtasks in some of the problems, so I highly recommend you to read all the problems.

I wish you high ratings in the new year!

Update: The contest is starting in 5 mins.

Scoring: 15-25-60-70

The contest has ended, congrats to the winners:

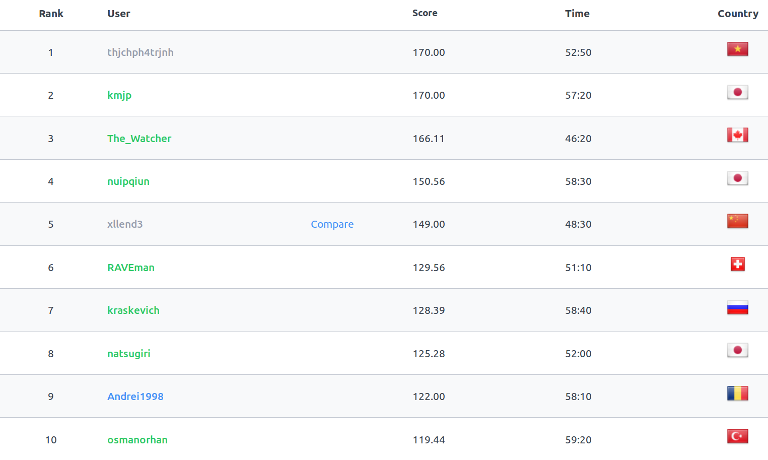
The editorials are live, ratings are being updated.

Please wait for 6-8 weeks for the prizes.

Happy Coding!

  • Vote: I like it
  • +51
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can somebody say please, what is complexity of this code?

http://pastebin.com/dwHJKAHs

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it -10 Vote: I do not like it

    I think it's O(N2log(N)). You should use some unordered hash to avoid sorting!

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it 
      for (j = 1; j <= n; j++)
            if (c[j] == 1)
               magical_dfs(j, 1, -1);

      I am interested, what is complexity of this part of code. From first look it's O(n2), but I am sure, that it's smaller(something like O(n·sqrt(n))), and that leads to O(n2·sqrt(n)) overall.

      → Reply
»
8 years ago, # |
  Vote: I like it +18 Vote: I do not like it

How can we check if two trees are isomorphic without hashing?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    The basic idea is to get the unique string of parentheses that represents the tree, for example: (()()) is a binary tree. But instead of sorting and returning large strings as we sort the children's strings, concatenate them, and add two characters each time, we may map each string into an ID, this way we return only one integer.

    () will have the ID 0.

    0,0 -which is (()())- will have the ID 1.

    Two rooted trees are isomorphic if they have the same ID. The following function returns the ID of the tree rooted at a starting vertex.

    int ID=1;
map<vector<int>,int> mp;
int DFS(int u,int parent){
   vector<int> ret;
   for(int i=0;i<graph[u].size();++i)
      if(graph[u][i]!=parent)
         ret.push_back(DFS(graph[u][i],u));
   sort(ret.begin(),ret.end());
   int &id=mp[ret];
   if(id==0)
      id=ID++;
   return id;
}

    Instead of using a map, you may use hashing.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      "without hashing"

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        You can find two solutions in my comment that don't use hashing. What I wanted to say in the last line is that hashing is just a small modification to the "without hashing" solution.

        → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      This doesn't work, because the value depends on root of the dfs tree. It works if you start your dfs from centroid of the tree though.

      → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

Solution to "Magic Number Tree"?

EDIT: Typed 2 instead of 1 in the mod function :/

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem C: Is it's main idea DFS with tricky recalculation answer for childs into answer for root?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    I will call sum of weights of edges on the path weight length of the path and amount of edges on the path edge length of the path.

    For every path between vertices we can calculate probability that its weight length will be added to the answer (for path of edge length l it is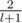 (because this path counts iff the vertex on it that gets deleted first is one of the ends)). Now we do n bfs-es and sum for all unordered pairs of different vertices (also you should not forget to multiply answer by n!).

    → Reply
»
8 years ago, # |
  Vote: I like it +19 Vote: I do not like it

Please wait for 6-8 weeks for the prizes

I got in top-10 in HourRank Jan 2016, but still haven't got a T-shirt. Is there any hope?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Unfortunately, the problem is you are from Russia and it's not possible to deliver t-shirts there. Sorry on behalf of the t-shirt vendors.

    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it -7 Vote: I do not like it

What is needed and enough condition for isomorphic trees ?

I tried with degree of nodes, but I got WA...

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain how did we get the probability that a path between 2 nodes with k intermediate nodes would be included in the third question a bit more intuitively?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +3 Vote: I do not like it

    You don't need probability for this problem. Just precalculate distance and no. of nodes between every two nodes.

    Then precalculate the number of permutations for a particular value 'd' such that the permutaions between two fixed nodes ( having 'd' nodes between them on the path in the tree ) has none of those nodes before the two fixed nodes in that permutation.

    eg: if nodes 2 and 3 have d=2 nodes between them in the given tree {4,5}, and N = 5, then some of the valid permutations will be 12345, 21345, 32415, etc. Basically, {4,5} won't come before neither 2 nor 3 in the permutation.

    Then ans += permutations[ nodes_between_path[u][v] ] * dist[u][v]

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

related to second problem how to solve for x and y for this equation ax+by=d (x,y>=0)?

→ Reply
»
8 years ago, # |
  Vote: I like it +14 Vote: I do not like it

My solution for C:

Consider any path between two nodes. We need to calculate how many times the weight of this path is added to the answer. Let the nodes be i and j. Then the nodes between i and j on the path and j must lie on the right of i in a permutation. Let the number of nodes on the path including j and not i be k, then the number of such permutations are:

Multiply this with the weight of path and add it to the answer.

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

For problem A, I got WA on test# 4.

Then I have downloaded the input and expected output for test# 4. Expected output is 20 1 and my code's output is also 20 1

So why I got WA on test# 4 ?

Upd: here is my code: http://ideone.com/V2I04T

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Print the value of m, I think it's 1 and you are accessing a[1]. But that is not initialized.

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Hi! Can someone please explain why centroid of the subtree is used for hashing? Is there any other way to hash a tree? Thanks! :)

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    Good day to you.

    Well you have a tree — you know nothing about — and you have to determine a point which is similar for all such trees == centroid(s).

    You would have to determine such point (any other) /or/ do it for all points.

    Good Luck & Have Nice Day! :)

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Hi! :)

      Thanks for the explanation. I think I see why this works. BTW, is hashing a tree some standard technique? Are there any similar problems?

      → Reply