Sorry for my poor English, this blog will be corrected soon.
214A - System of Equations
Solution for this problem — just go through the possible pairs of numbers and check them for correctness. We can do that in any way.
214B - Hometask
Nuber is divisible by 2,3,5 only if sum of the digits is divisible by 3 and last digit is 0, so if we havent 0 in our set answer is -1, otherwise solution exists(we can return 0 as solution). A further solution — analysis of the cases.
Lets sort all didgits in nonincreasing order. If sum of all digits is divisible by 3 — answer is our set of digits(without spaces ofcourse :) ). If modulo equals 1 — we must delete minimum digit from out set with modulo after division by 3 equals 1, if we haven't such we must delete 2 minimal digits with modulo after division by 3 equals 2. If we have modulo equals 2 — we have identical case.
Also we must remember that we cannot use leading zeros. In case when we have more then one 0 and no another digit we must print only one zero.
213A - Game
Solution — Greedy.
Lets our computers settled on circle, and moves (1->2, 2->3, 3->1) will be steps "forward", and moves (1->3,3->2,2->1) will steps "back".
Note that "back" moves is not optimal, as we can make two moves "forward" that is identical in time. We will look over all starts. Further, we will go by circle while we not complited all game. For every level we will remember number ne[i] — count of another level that "direct" need for it. We will complited levels with ne[i]=0 and update all ne[i] that we must. It can be implemented with O(n^3) time.
213B - Numbers
Solution — dynamic programming.
Look over for length of the number that we will build. Further, we will use DP f(len,i) — how many numbers with length len we can make with digits i..9.
Recount:
- f(len,0) = sum(f(len-i,1)*C(len-1,i), i=a[0]..len);
- f(len,j) = sum(f(len-i,j+1)*C(len,i), i=a[j]..len), 0<j<9;
- f(len,9) = 1, если len>=a[9], 0 если len<a[9].
C(n,k) — binomial coefficient.
213C - Relay Race
Solution — dynamic programming.
Note, that we can make 2 pathes form cell (1,1) to cell (n,n).
Note, that after each move our cells will be located on the same diagonal.
We will solve the problem with DP f(d,i1,i2), d — diagonal number, i1 — 1st coordinate 1st path, i2 — 1st coordinate 2nd path. It is clear that we can calculate 2nd coordinate when we know number of the diagonal and 1st coordinate. Recount — obvious, we make all 4 transition, and if pathes are intersected in temporary point, we add value of the cell only one, otherwise we add both values of the cells. We can imlement this solution with O(n^2) memory if we will rewrite array of DP after increasing of diagonal number. Also we must remember that answer can be lower then 0.
213D - Stars
I present solution as few pictures:
https://get.google.com/albumarchive/pwa/115317317397602031319/Solutions131
Implementation.
We have only one difficult moment — how to count coordinates? We can calculate them from regular pentagon, all that you need, you can read there.
213E - Two Permutations
For given two permutation we will make two another by next transformation: New_A[A[i]] = i, where New_A — news permutation, A — given permutation. Lets we get two permutation A and B. Now our problem is next: how many sub-arrays of length n are equals to firs permutation. Two arrays will be equal if after swaping every element with its number in sorted array obtained arrays will be element-wise equal.
Further solution hashes, but we will use not only modulo 2^64, we will use some big modulos, but they must be smaller then 2^32-1.
Lets step[i] = 1000003^i.
Lets F(A) = num[1]*step[1] + num[2]*step[2] + ... + num[n]*step[n], where num[i] — number of the element A[i] in sorted array.
If we will compare arrays, we can use this function. But it can be very big, so we will count it by modulos.
So now our problem is to calculate F function to every subarray. Lets look what will change after adding/deleting some elent from set: some element from num array willnot change, and some will become grater after adding, and become lower after deleting. So we must use some interval-tree to recount our F function. We need to know sum of step[i] on some interval of added numbers and count of elements on some interval. Uses this information we can simply recount out function. Also we must remember that after adding element with coeficinet step[i], where i>n and deleting some previos element our function will become grater that we need. So we will multiple hash of first array by 1000003 to avoid this issue.











Sereja , thanks for writing the editorial. Can you explain solution to 213C(Relay) more detailed? Using the English version translated by Google, I was confused.
It would be better if you submit your reference solutions with proper comments.
I would be appreciated if someone explains the idea behind Petr's solution to 213C, especially what the state best[][] means and how the transferring works, note that it's 2d(two dimensional) instead of 3d used by most contestants which reduced a lot of memory.
Most contestants use best[step][x1][x2], but you only need to know best[step-1][][] when you are calculating best[step][][], which means you don't need to store best[x] (x < step-1). So you can compress best[MAXSTEP][][] to best[2][][], or like Petr use best[][] best1[][].
in 213B f(len,i) is equal to the quantity of numbers we can build using digits i..9 of length len.but why do we multiple in formulas for example f(len-i,1)*C(len,i),should not it be f(len-i,j+1)*C(len,i),please tell me where's my mistake,thanks in advance
I think it should be j + 1 too.
It would be nice to see a visualisation of some interesting solutions for stars (div1 D).
I think it's difficult for me and I cannot understand it yet...= =
This is another easy solution for problem D: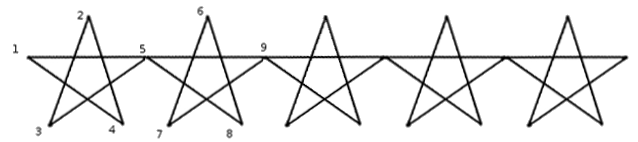
Assume that the distance between 2 vertices (1-5) is len. After pre-computing the positions of 4 vertices 1 2 3 4, positions of others vertices can be calculated easily by adding k * len to the x coordinate of the first 4 stars (for example, if we know (x3, y3), then (x7, y7) = (x3 + len, y3))
To draw the stars, for example, with n = 2, we can do like this: 1 5 9 7 6 8 5 3 2 4 1.
Nice solution.
In the example of problem E,why "1 3 5 2 4 1"is correct but "1 4 2 5 3 1"is wrong? I just output them in an opposite way.
Sorry ,it's problem D
I think the time complexicity for 213A is O(3*N^2)(N^2), not O(N^3)
Well, O(N^2) is a subset of O(N^3) :), but you're right, the time complexity of the algorithm described by Sereja is O(N^2).
It will work O(n^2) only if we will find all zeros(when there is not any edge to the vertex) quickly. Of course it is easy. But my solution works O(N^3) at worst case.
It is A problem, so I think that it is normal, when such solution can passed system tests.
Are you sure that it's O(N^3)? When we go around 3 computers, we'll always find at least one zero, so we'll perform O(N) loops. Since you maintain a degree array (and I'm very sure that you also use a boolean array of visited vertices), it's possible to find a zero in O(N). And for each zero you decrease O(N) items in the degrees array. The result is O(N) * (O(N) + O(N)) = O(N^2). What have I missed?
Yes, you are right :)
In problem 213E,I have a question. when you use hash,why do you choose 1000003,and it is likely that F(A) you define exceeds long long? What should you do to avoid the problem.
1). I use 1000003, becouse it's bigger then 200000 and prime. 2). I use long long's overflow (it's the same as get number modulo 2^64), but I also use hashes by some other modulos.
Does it possible that the hash crashes,that is to say,two different permutations have the same number modulo 2^64 ? But I notice that most people don't consider it.
Yes, it can be.
So I get an AC, But how should we improve it?
We can calculate hashes by modulos 1000000007 and 1000000009 instead of 2^64.
Can you assure that it doesn't crash if you use 1000000007 and 1000000009 as modulos. Also we can't store the permutations who crash.
We can't assume that. Hashes give big probability, but not 100%.
Ok,Thank you,I get an AC using 1000000007 as the modulo a moment ago,
In div2 B-Hometask, after ensuring there is a 0 in the list, I tried to find the maximum digits I can keep which will give me a sum % 3 == 0 using Knapsack DP. Here is my code Code. I got WA on test case 13. All I want to know, did I get WA due to stack overflow? Or is it not possible to find which digits to keep using Knapsack dp? Also, if stack overflow occurs in codeforces, do we get WA or run-time error?
I can't understand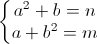 So it means:
So it means:
(a-b)(a+b-1)=n-mif n==m, a=b is a true answer that consists of infinite pairs. What is wrong with my insight? (problem A)not every solution of (a - b)(a + b - 1) = n - m is the solution of this system. Futhermore, the number of solutions of the system is finite, because if a > n or b > n then a2 + b > n
Can someone please explain in detail(in English) the editorial for div1 B?
comment deleted
Can someone give a proper explanation for 213C Relay Race . What does the author mean by "There are 2 paths from (1,1) to (n,n)" and also "after each move our cells will be located on the same diagonal."
Consider Rubik also starts from (1,1) and moves to (n,n) . (this will not change answer ) .
The diagonals refer these --.
Clearly at each step both will be on same diagonal
Knowing the diagonal number , and x-coordinate , you can get y = d-x + 1.
So , we store only diagonal number and x-coordinates for both rubik and furik
33898588