I've participated in JOI 2017 and I'm trying to find the solutions in English. Why don't we create a tutorial with brief explainings of the solutions? I'll contribute by posting the two problems I have solved during the contest, but I'll update when people comment solutions.
If someone speaks Japanese, the official JOI website has posted solutions, but they're only available in Japanese, so you could translate a brief explanation to us :)
Links for problem statements (English) are available below. Could you help rng_58?
Keep an array of differences between consecutive heights, so that delta[i]=A[i]-A[i-1]. Keep the sum of the values of positive differences in a variable pos, and the sum of the absolute values of negative differences in a variable neg. Each time you update a range (l,r), adding X to it, you just need to update differences l and r+1. To update difference i, you reduce its absolute value from pos or neg, depending on its signal, add X to it and adds its absolute value to pos or neg. After each query, the answer will be neg*T-pos*S. Don't forget to use long long.
You have to create K-M stops for the semiexpress line (besides the M fixed ones). For each range between two consecutive express stops, analyze the advantage of creating a semiexpress stop on each station of the range. You can easily calculate what are the stations in that range that one can achieve within time T using only the express and local trains. Call the last station of this range i. Check how many new stations one could achieve if the semiexpress train stopped at station i+1. Call it Q. Then, keep this value on a heap. After it, check the new number of stations you could achieve if, after it, you created a new stop at station i+1+Q and add to the heap again. Update the values of i and Q and repeat it at most K-M times (because it's the number of stops you can create), or until the value of i exceed the limits of the range you're analyzing.
After this, your answer will be all the stations one can reach with express and local trains plus the K-M greatest values of the heap.
Problem 3 — solution posted by kokosha
Observation 1 — Let's take a look at the point with the minimal value(X) and maximal value(Y). If these two values are inside the territory of JOI or IOI, we are done. So these two values are in different territories.
Now we have two territories, one with minimal value and the other with maximal value.
We can start the territory of minimal value in one of the four corners of the rectangle, or we can simply rotate the rectangle by 90 degrees. Let make the start point the left-top corner
Fact 1 — Suppose the value of answer is K, then the numbers in minimal value territory are less than X+K, and the numbers in the maximal value territory are bigger than Y-K.
Using this we can use binary search on the answer, using the following greedy algorithm.
Fix a column position, the rightest one, this will help us to generate the maximal value territory.
Now we will generate the minimal value territory.
For each row from top to bottom, find the leftiest position that satisfy less than X+K.
If the leftiest position is before to the column position, set the column position to the leftiest position and verify the maximal value territory from new column position to old column position and the rows below.
If the leftiest position is after or equal to the column position, set the leftiest position to the column position.
Credits to tozangezan — http://www.ioi-jp.org/joi/2016/2017-ho/2017-ho-t3-review.pdf
Waiting for comments
Waiting for comments











Problem 3
Observation 1 — Let's take a look at the point with the minimal value(X) and maximal value(Y). If this two values are inside the territory of JOI or IOI, we are done. So this two values are on different territory.
Now we have two territory, one with minimal value and the other with maximal value.
We can start the territory of minimal value in one of the four corners of the rectangle, or we can simply rotate the rectangle by 90 degrees. Let make the start point the left-top corner
Fact 1 — Suppose the value of answer is K, than the numbers in minimal value territory is less than X+K, and the numbers in the maximal value territory is bigger than Y-K.
Using this we can use binary search on answer, using the following greedy algorithm.
Fix a column position, the rightest one, this will help us to generate the maximal value territory.
Now we will generate the minimal value territory.
For each row from top to bottom, find the leftiest position that satisfy less than X+K.
If leftiest position are before to the column position, set the column position to the leftiest position and verify the maximal value territory from new column position to old column position and the rows belows.
If leftiest position are after or equal to the column position, set the leftiest position to the column position.
Credits to tozangezan — http://www.ioi-jp.org/joi/2016/2017-ho/2017-ho-t3-review.pdf
Alternately, you can use segment tree to solve P1 in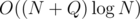 .
.
Store answer for a range, leftmost value and right most value in a node. Combine can be done by adding individual answers and comparing rightmost element of left range and leftmost element of right range. Use lazy propagation for updates.
Problem 4:
5 points is very easy.
35 points is O(N^2) dijkstra.
You can do that people is vertices, and edge is pair of people and cost can be calculated for N=2 case.
I'm sorry that I can't explain 100-point-solution because it is very hard to solve (I can't solve it).
Consider the path of the ball.
One player comes to the ball, moves a distance, and then kicks the ball away. This process repeats, until the ball reaches the destination.
It's obvious that each player acts at most once, or it's not optimum.
How to build the graph?
There are 3 kinds of actions for a player with the ball:
For each point (x, y), create 3 vertices — v1(x, y), v2(x, y), v3(x, y) — indicating these actions.
A player can kick the ball away, so we create 2 directed edges from v3(x, y) to v1(x, y) and v2(x, y) with weight B.
v1 means kicking along x axis, so we create an undirected edge between v1(x, y) and v1(x + 1, y) with weight A. It's similar for v2.
v3 means moving with the ball, so we create 2 undirected edges between v3(x, y) and v3(x + 1, y), and between v3(x, y) and v3(x, y + 1), with weight C.
The ball can stop and another player comes to the ball, so we create an directed edge from v1(x, y) and v2(x, y) to v3(x, y) with weight C × d(x, y), where d(x, y) is the distance between (x, y) to the nearest player.
Then the shortest path from v3 of player 1 to v3 of player N is the answer.
How to solve the problem E?