rhezo's blog

Codechef Long Challenge problem DISTNUM3
By rhezo, history, 8 years ago, In English

How to solve this problem?

Statement: Given N nodes of a tree, answer Q queries of 2 types(update value of some node or find the number of distinct numbers on the path from U to V).

There is a solution with Mo's algorithm with updates and I don't understand that as well. Can anyone explain any other approach or even this one?

  • Vote: I like it
  • +10
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by rhezo (previous revision, new revision, compare).

→ Reply
»
8 years ago, # |
  Vote: I like it +15 Vote: I do not like it

Update query on Mo
Mo on trees
Maybe these links can help you.

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +23 Vote: I do not like it

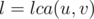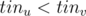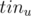Perform a DFS of the tree and obtain the dfs start and end times , if a query is from to , let . Assume . If then query is from to 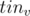else query is from 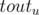to 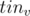along with . You need the frequency of elements from this range whos nodes appear exactly once in the range , to do that , break the array into 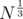blocks , and for each pair of blocks , calculate the frequency table ans the answer for that block. Now each query can be brocken in to a prefix + a pair of block + a suffix. The size of the prefix and suffix is atmost 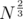So add those elements by brute. To do an update traverse each pair once and update the frequency table accordingly. Total Complexity .

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

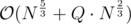    The problem is almost the same as this problem, and can be solved with the same complexity in a manner very similar to Mo's algorithm by sorting the queries via <starting block, ending block, time of query>, where starting and ending blocks are the blocks which the first and last elements of the query belong to, respectively. Code for this problem: Link.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I understood the entire logic from your code but I have one doubt about the update queries. If the queries are given in this order :

      RQ1, RQ2, UP1, UP2, UP3, UP4, RQ3, RQ4
      (RQ is a range query and UP is an update query).

      When the range queries are sorted if the order we get is :

      RQ3, RQ1, RQ4, RQ2,

      then all the update queries will be processed for every range query. This would lead to O(Q^2).

      Please correct me if I am wrong.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        All range queries are sorted according to the tuple: <starting block, ending block, time of query> ( meaning first sort by starting block, then by ending block, and finally by time of query. ) Notice that the number of distinct values of the tuple <starting block, ending block> are N2 / 3, and all Range Queries with the same value of <starting block, ending block> will be sorted in the increasing order of time of query. The Q updates need to be processed only once for this group of queries. Hence total number of times we need to perform update is: Q * N2 / 3 , not Q2 . You can refer code to see how to perform these updates.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it +1 Vote: I do not like it

          Very nice explanation. Thanks a lot!

          → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I saw your solution and understood everything! Thanks a lot :)

    → Reply
»
8 years ago, # |
  Vote: I like it +11 Vote: I do not like it

Hey.
Can anyone give me a link to a problem which is solvable with Mo's algoritm on array with updates? I'd like to practice this method.

→ Reply