In the Editorial "Divide by Zero and Codeforces Round #399 (Div. 1+2, combined)" the problem setter said PROBLEM B can be solved easily by using DIVIDE AND CONQUER strategy. How to learn this strategy????
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 151 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Dec/23/2024 06:26:24 (j3).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Just play a lot.
Usually in the problems of divide and conquer you should divide the problem into several similar and disjoint parts, can be in two equal parts, and find an interesting property in the middle so that you can continue reducing the problem, or joining these parts to have a final result, i.e. if you build a convex hull with a divide and conquer approach, you would first think about dividing it in half, and you suppose you can build the major convex hull with the two parts, then The serious question is: how would you do to join them?, there is a form with complexity O(n),
thus obtaining an O(nlgn) algorithm, since time is T(n) = 2*T ( ) + O(n), but I will not end this. Instead if I want find the square root of x, then I can search: "The greatest number v such that v * v <= x", so if I analyze in the middle of the interval [0, x], v =
) + O(n), but I will not end this. Instead if I want find the square root of x, then I can search: "The greatest number v such that v * v <= x", so if I analyze in the middle of the interval [0, x], v =  , then this may be my answer or it can be < , in the first case I continue whit interval [0, (
, then this may be my answer or it can be < , in the first case I continue whit interval [0, ( )] and otherwise in the interval [(
)] and otherwise in the interval [(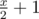 ), x], so I just look at O(log(n)) intervals. The execution time is T(x) = T(
), x], so I just look at O(log(n)) intervals. The execution time is T(x) = T( ) + 1, then T(x) = O(log(x)).
) + 1, then T(x) = O(log(x)).
In the problem B, you divide the problem of the interval [1, 2k - 1] where k is the most significant bit plus 1, i.e if n = 8, then k = 4. In the intervals [1, 2k - 1 - 1] and [2k - 1 + 1, 2k - 1] and I verify in the point {2k - 1}, where it should be the first bit of n, and add this if is in the range [l, r] and continue...
My English is not the best, I hope it has been understood.
my submission: http://codeforces.net/contest/768/submission/24854078
of course, if you analize the interval [a, b] and is disjoint to interval [l, r], then return, this it is very important to complexity...
Thanks for your comments. Now I have realized how to deal with that.