Блог пользователя marlonbymendes

Why do we add the least significant bit while updating some index in Fenwick trees?
Автор marlonbymendes, история, 8 лет назад, По-английски

Several guides explain how Fenwick trees (BIT) work (and they do it pretty well), but I don't see any intuition or proof on it's correctness, specially the update operation. I've used BIT before and I know "how" it works, but not "why" the update operation works.

Here's the usual update code, taken from Topcoder's tutorial.

void update(int idx ,int val){
    while (idx <= MaxVal){
        tree[idx] += val;
        idx += (idx & -idx);
    }
}

Popular guides on BIT (don't actually answer the "why" question):

Topcoder

GeeksForGeeks

Tushar Roy's video

Also, pllk recent book, page 86. Link

  • Проголосовать: нравится
  • +28
  • Проголосовать: не нравится

»
8 лет назад, # |
  Проголосовать: нравится +1 Проголосовать: не нравится

This answers the question. Watch it till the end, helped me a lot in understanding BIT

→ Ответить
  • »
    »
    8 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    Thanks for your answer. Which moment (minutes:seconds) the video explains the intuition or proof on BIT correctness? Thanks

    → Ответить
    • »
      »
      »
      8 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится

      I think you need to watch the whole of the video :/ And also, its not a concrete proof of correctness. For that you will need this
      Other than that, the video gives a good intuition about the structure and its not a waste of time :D

      → Ответить
      • »
        »
        »
        »
        8 лет назад, # ^ |
          Проголосовать: нравится 0 Проголосовать: не нравится

        I watched the whole video. The guy just explains some examples, this is not a intuitive or proof on "why" BIT work, only "how". Several guides already do that (see blog). The paper you linked seems to be more rigorous on that matter, I'll check that later, thanks!

        → Ответить
»
8 лет назад, # |
← Rev. 7   Проголосовать: нравится +9 Проголосовать: не нравится

This graphic helps a lot (I used it to get intuition about BIT), and it is the best of all that you can find in the internet because it shows which fenwick tree position represent which range clearly. (While other graphics do not)

It will be better if the decimal numbers where in binary but, it was the best I found.

Imagine you need to update 5, in binary 00101 (we are using fenwick with 2^4 memories). You need to update all ranges that include that 5, because if 5 increases then all ranges that contain index 5 are increased.

I don't know the formal proof, but if increase the least significant bit of 00101 progressively you get

  • 00101 => 5

  • 00110 (00101+00001) => 6

  • 01000 (00110+00010) => 8

  • 10000 (01000+01000) => 16

And if you look in the graphic, that are the ranges that 5 touches, 5,6,8,16. (The upper position of each range)

You can apply the same logic I used

  • To any index you want to increment
  • Using the query operation (you'll see that you get the disjoint sum of ranges that cover all values lower or equal)
→ Ответить
  • »
    »
    8 лет назад, # ^ |
      Проголосовать: нравится +1 Проголосовать: не нравится

    Thanks for your answer. As I said in the blog, I know "how" bit works so I know that you add the least significant bit to itself you'll cover all ranges in the graphic. The question is, why is it that operation cover all (and only) ranges that will ever use index 5 (in your example)? This is not obvious once the BIT's size increases.

    → Ответить
    • »
      »
      »
      8 лет назад, # ^ |
      ← Rev. 8   Проголосовать: нравится +2 Проголосовать: не нравится

      well, each fenwick position on position i covers the range [i - (i& - i) + 1, i] for example position 01011000 covers

      • 01010001
      • 01010010
      • 01010011
      • 01010100
      • 01010101
      • 01010110
      • 01010111
      • 01011000

      Note that if we add the least significant bit of any of these numbers constantly (except the last, that does not need to add nothing) then we will arrive (in more or less steps) to the original 01011000. Which means that every number in the interval will eventually generate the interval index using the query operation. (This is not a proof, only an idea).

      So If this idea is true (I don't know the proof), and we generalize it then for every interval all values included by definition will reference the interval in some query step.

      • Number is on interval => Number generates its index on query (1)

      So we need to show that every interval that an index generates in a query will include the number (that is the reciprocal property).

      Again I won't make proof but an idea.

      Imagine we have a random number, lets say 01010100. It is clear that if we add the lower one bit several times we will get a higher number. This means that the upper end of the interval will be over the number (or equal if we don't add the lower one bit never). So we need to show that the lower end of the interval will be lower or equal to the number.

      Which is the lower end of the interval? As at said at the beginning it is (i& - i) + 1

      is this number lower or equal to the original number? Or in code

      a = some index
b = a
while 1:
    b += b&(-b) 
    is ( b - b&(-b) + 1 >= a) ?

      Is the invariant true for the 'infinite' program?

      We can see that the property is true one paper (try to make the operations) because if we add the lower one bit of a number several times, we will make several carries to the left but then remove that carry (or even worse, a more significant one), so we are certain the final number will be lower or equal than the original. Of course we will also add 1, but it won't make any problem, please make the operations in paper and you will see that the invariant holds.

      Image for better understanding

      So as this two properties are true, we have

      • If a index is member of an interval => index calls interval on query (1)
      • If an index calls interval on query => the number is on the interval (2)

      So the intervals referenced by an index query are always every one valid, and there aren't any more than them because, if it were then it would exist an interval that would contain the index, and the index won't call the interval, which violates (1).

      Sorry if it is a bit obfuscated, but I don't have a proof and I only show some intuition of the two properties that hold to make fenwick work .

      → Ответить
      • »
        »
        »
        »
        8 лет назад, # ^ |
          Проголосовать: нравится +1 Проголосовать: не нравится

        Thanks for your intuitive view on the update operation, indeed I haven't seen this way of thinking before. I tried some examples on paper to understand your two properties, and they do hold and are intuitive, but I'm still "trusting" (believing that the properties work without proving them) in some level, which was the initial problem... I know that any example I come up with and do it manually the BIT will work, the problem is that I tried multiple examples by hand and it didn't give me any insight on the general idea on why BIT is correct. Anyway, thanks for your time, I appreciate that.

        → Ответить
        • »
          »
          »
          »
          »
          8 лет назад, # ^ |
          ← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

          Well, I think that with these ideas and hard work you are on the way to develop a proof, but you need to have experience and know how to do it rigorously. If you prove both properties, then fenwick is right!!

          Maybe try to find the fenwick tree original paper to search for it :)

          → Ответить
          • »
            »
            »
            »
            »
            »
            8 лет назад, # ^ |
              Проголосовать: нравится 0 Проголосовать: не нравится

            I did take a look on the original paper. It has no proof on correctness, only examples and figures.

            → Ответить
»
8 лет назад, # |
  Проголосовать: нравится +3 Проголосовать: не нравится

Let dec(a) = a  -  (a & -a) and inc(a) = a + (a & -a). Also, let dec{a} be the set of reachable values applying dec operation several times (including a) over a and inc{a} the same for inc.

We say that b is a prefix of a if b could be obtained from a after applying some number of dec operations (possibly zero) on a.

We need to prove that if we add v to some position y then for every x >= y the intersection between inc{y} and dec{x} have exactly one element.

It's true for x = y.

Suppose x > y. The binary representation of x and y will be (a0 is the left-most bit):

x = [a0, a1, .., ak - 1][1][bk + 1, bk + 2, .., bn - 1]

y = [a0, a1, .., ak - 1][0][ck + 1, ck + 2, .., cn - 1]

We need to consider two cases:

(1)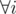 (k + 1  ≤  i  ≤  n  -  1) ci = 0

y is a prefix of x, so y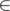 dec{x} and inc{y} dec{x}  ≠  . Also since y is a prefix of x, inc(y) > x (I'm lazy, but it's easy to prove) and the intersection have exactly one element.

(2)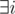 (k + 1  ≤  i  ≤  n  -  1) ci = 1

We can prove that after applying some inc operations, we will reach y' = [a0, a1, .., ak - 1][1][0, 0, .., 0] (again, it's just binary arithmetic). So y' will be a prefix of x and this is similar to (1).

This is not a complete proof because I skipped many details related to binary arithmetic.

→ Ответить
  • »
    »
    8 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    Thanks for your answer, only now I got the time to read and check it. I did understood the proofs (1) and (2) however I'm afraid that these cases are not general enough.

    For example, let's add 5 to position 12 in original the array. Now we have to update the BIT in positions inc{y}

    v = 5, y = 12

    12 = 1100 (binary)

    inc(12) = 1100 + 100 = 10000

    You said "every x >= y the intersection between inc{y} and dec{x} have exactly one element.", but for x = 10000 > y = 1100 the intersection between inc{y = 12} and dec{x = 16} is empty, i.e 12 is not a prefix of 16. That example doesn't fit in formats (1) and (2).

    → Ответить
»
12 месяцев назад, # |
  Проголосовать: нравится +8 Проголосовать: не нравится

Good question! It puzzled me as well for a while, so I guess this goes to show how deceivingly simple implementations might have pretty hard explainations. I will try to explain my "proof" (I haven't seen one either).

Consider the following image of a Fenwick Tree (source: cp-algorithms):

In particular, watch how the first three levels look like a Fenwick tree over the array of "ranges over two consecutive elements". We will exploit this.

Let's consider a position $$$i$$$. We have two cases:

  1. $$$i$$$ is odd. Then, we update the "single position" $$$i$$$ and increment $$$i$$$ by $$$1$$$
  2. $$$i$$$ is even. In this case, it's not on the lowest level, so it must reside on the "higher-order" Fenwick Tree of ranges of two consecutive elements. In this (imaginary) Fenwick tree, the corresponding index is $$$i/2$$$.

You can see that what we're basically doing is we "divide by 2" up until $$$i$$$ is odd, at which point we found the corresponding level of $$$i$$$. Then, we update, increment $$$i$$$ by $$$1$$$ and continue. This "increment by lowest bit of $$$i$$$" is basically doing that, only by skipping the "divide by 2" parts. I know it's a bit hand-wavy, but I think it shouldn't be too hard to formalize a proof from this.

→ Ответить