Invitation to NAIPC 2017 / Grand Prix of America

8 years ago, # |

+36

How is it related to ICPC? Will North American teams be selected based on this contest?

→ Reply

8 years ago, # ^ |

+36

This started as a contest for North American ICPC teams. It used to have some big prizes but since we don't have many sponsors currently, it is mostly just for fun now. It's meant as some more practice before WF, and is not used for any kind of selection.

→ Reply

tehqin

8 years ago, # ^ |

+55

No teams are selected from this contest this year.

North America is trying to form a super regional for WF selection sometime in the future (something like NEERC). This contest is a stepping stone to that end.

Right now the contest is a WF preparation contest. The target is an ICPC WF level set to prepare teams for the difficulty and pressure of ICPC WF. (Or that's what I've been told anyways.) It used to be an onsite invitational contest (at UChicago) for teams going to ICPC World Finals but due to lack of sponsorship in recent years is an online only contest.

→ Reply

SoSad

8 years ago, # |

Will there be a gym mirror？

→ Reply

aajjbb

8 years ago, # |

Contest is over and results are here .

→ Reply

8 years ago, # |

+46

How do you estimate how fast flow works?

I believe G is a flow problem. There are various ways to construct a graph, and also there are various flow algorithms. What is a good way to choose them? (Big-O analysis is not very useful here)

→ Reply

8 years ago, # ^ |

+31

Distance from source to sink is rather small here, so I believe Dinic will be the best one. Network usually should be chosen such that number of edges is as small as possible. In this problem we used network with about 10⁶ edges.

→ Reply

duyboy135

8 years ago, # ^ |

Can you describe more about your network?

→ Reply

8 years ago, # ^ |

← Rev. 7 →

+18

Make nodes for every horizontal segment, it could be done straightforward using nm³ / 6 edges or in segment tree-like technic using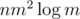 $\text{[math]}$ edges.

Then we made something like sparse table over each group on n segments having the same left and right ends. It cost us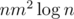 $\text{[math]}$ edges. Then each customer has 2 edges.

P.S. Now I realized that first part could be done like sparse table too. In that case it will consist of nm² edges

→ Reply

8 years ago, # ^ |

Just sparse table (2dimensional) is enough to get 0.5 running time

→ Reply

8 years ago, # ^ |

I tried to create such solution, but it has more edges and its implementation looked for me more tricky.

→ Reply

8 years ago, # ^ |

← Rev. 2 →

Why? It has 2 * n * m * 5 * 5 + k * 4 + n * m edges

→ Reply

8 years ago, # ^ |

+43

Sadly, the data for G was extremely weak to the point that very naive greedy solutions passed the data. This caused the Dinic to find a solution on its first iteration and simply break out very early. I have been working on generating some stronger data and have got something that takes >10 seconds. This is more than double the timelimit allotted for this problem.

→ Reply

Kostroma

8 years ago, # ^ |

+14

Here comes the question to the authors: how did they decide to make such constraints? Why weren't there strong tests on the contest? Haven't they had a doubt when preparing the problem, that on some tests this solution might be working too long?

→ Reply

8 years ago, # ^ |

Initially the bounds were set at k = 1,000. However the data was weak and naive flow solutions that should TLE passed in time. Thus they raised the bounds. However, they failed to consider that the data was just weak and not that this flow graph just runs fast. (It doesn't if you make good cases)

→ Reply

8 years ago, # ^ |

Interestingly, for this problem, I found [Ahuja-Orlin's](http://dx.doi.org/10.1002/1520-6750(199106)38:3<413::AID-NAV3220380310>3.0.CO;2-J) variant of Edmonds-Karp algorithm faster than Dinic's (passing in 2.4s whereas Dinic's times out). See: "Distance-directed augmenting path algorithms for maximum flow and parametric maximum flow problems"

This is with a Java implementations of Ahuja-Orlin and of Dinic that are fast enough to both pass fastflow on SPOJ.

My worst case is market-1001.in with 421,200 nodes and 1,622,129 edges. I do not believe that I am building the network optimally. Could someone share how many nodes/edges you get for market-1001.min?

I can also pass using zeliboba's "straightforward" approach of using just horizontal segments, which produces 102,552 nodes and 5,105,000 edges for market-1006.in and again passes with Ahuja-Orlin only.

→ Reply

8 years ago, # ^ |

You want to create a 2D sparse table. This will create a smaller graph. However, the data for G is still relatively weak.

Try these cases: https://drive.google.com/open?id=0BzaDgSP3MuIGcGdvNVc5c0R3NXM

I have created 52 cases which cause even the judge solutions to TLE.

→ Reply

8 years ago, # ^ |

Can you describe further what you mean by "sparse table"? Are you suggesting to build a network with multiple layers for powers of 2, each representing successively smaller quadratic (2ⁱ × 2ⁱ) portion of the entire market? Analogous say to the technique to do a 2D RMQ in O(1) with $\text{[math]}$ precomputation?

Wouldn't that require up to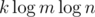 $\text{[math]}$ edges? In other words, would each customer's nodes be linked to the largest squares covering the customer's area?

→ Reply

8 years ago, # ^ |

A normal sparse table (used in RMQ) creates log n ranges from every possible left point allowing queries eith only 2 lookups. You can do this in two dimensions by brute forcing a top left corner (do all top left corners) and then having log n widths and log m heights. This creates n*m*log n*log m different nodes in your sparse table. Then, each customer only needs to connect to 4 of these nodes to cover his entire range. You also want to be careful while creating edges from stores to your sparse table nodes. You want to do layering similar to how RMQ generstes its table. This will minimize the number of edges you need to add.

→ Reply

8 years ago, # ^ |

So with this approach I pass in 1s on Kattis (159,051 nodes and 615,598 edges for market-1006.in), but (a) Dinic still times out (only Ahuja/Orlin's improved shortest augmenting path passes) and (b) I still take about 14s for your additional test cases. I assume your network is immune to a bad choice of maxflow algorithm?

How do you connect layer to layer? I tried connecting using 4 edges from layer (2ⁱ, 2^j) to layer (2^i - 1, 2^j - 1) as well as just connecting using 2 edges to (2^i - 1, 2^j) or (2ⁱ, 2^j - 1). My (2⁰, 2⁰) layer are the stores themselves which are connected to the sink. I also optimized out redundant edges when a customer x or y range is a power of 2.

Are further optimizations necessary? What do you mean by "careful while creating edges"?

→ Reply

7 years ago, # ^ |

The data I made should hopefully make any flow solution TLE. The bounds for this problem were just way too large and it is not possible to get a flow solution to pass good data. The data on Kattis, however, is very weak and greedy solutions pass it. Thus, you will want a flow which will find some answer and break early if it realizes that answer is already optimal. As far as I knoe, some implementations of Dinic will do just that but you may just have to get lucky on its choices. Ultimately, the data is just too big and it may just not be possible to get your flow to run in time because the way youbare saying you construct the graph sounds right to me.

→ Reply

7 years ago, # ^ |

I see. Looks like I got it now. Here's something else I learned: for both Dinic and Push/Relabel with FIFO and Gap heuristics, it matters in which direction you construct the network. I had connected the source to the customers and the markets to the sink.

When I switched it to connect the source to the markets, both Dinic and PushRelabel passed on Kattis with less than 2s. Whereas under Ahuja/Orlin it didn't matter which direction the network was constructed. That's something I hadn't known.

FWIW, the slowest of your additional test cases is case_112 which takes about 12s on my machine.

→ Reply

7 years ago, # ^ |

Yeah that makes sense. And yeah I was just generating random cases with certain special bounds to make things take long. I believe there exists a case which can make a solution take >60 seconds but it is probably super hard to construct. Even then, I have cases that cause even the judge solutions to TLE with 3x-5x the alotted time.

→ Reply

7 years ago, # ^ |

Is there a non-flow based solution that handles the problem bounds within the time limits for the worst case?

→ Reply

7 years ago, # ^ |

Not that I or the judges know of. The intended solution is the flow with 2-d sparse tables.

→ Reply

Nezzar

7 years ago, # ^ |

← Rev. 2 →

Maybe you can try this: https://puu.sh/vInRF/c27338e52d.txt It is a O(nm) construction but after reading comments above I'm not sure about the correctness (it passes the weak test cases tho)

UPD: yep, my solution is wrong, I have no idea how it passed system test wtf

→ Reply

7 years ago, # ^ |

Nezzar,

The system test data was very weak. It was randomly generated in such a way that stores were given way too much stock and the customers not enough requests. Thus, it was always optimal to simply greedily assign apples to customers as they ask for them. This obviously doesn't work. However, it does indeed pass the judge data.

Apparently what happened was that the bounds were initially k=1,000. However, because of the weak data, naive flow solutions (which should have TLE'd) ran in time. Thus, they simply kept raising the bounds until they got that solution to TLE. The judges, however, never considered that the data was just weak. They simply assumed there must be some special property in the graph which allows the flow to run fast. This sadly is not the case =(

→ Reply

8 years ago, # ^ |

← Rev. 5 →

+13

G is a flow problem with V = nmlgnlgm + k, E = 4k + 2nmlgnlgm. Also, someone I know wrote E = O(klgnlgm) (approx 15M edges) and passed. In this problem, I think author needed big constraint to force his solution (although, surprisingly, this failed.)

I was also curious about the time complexity of flow algorithm. This is the "fact" I know about time complexity of flow algorithm :

Ford fulkerson is O(NM^2), Dinic is O(N^2M). (You can solve a problem about making Dinic TLE with O(N^2M) operation, on here)
Both are O(fE) of course
If it have unit edge capacity, Dinic runs in O(M^1.5). This was proposed in some CF round in last year.

This was what people usually say about time complexity of flow algorithm :

Ford fulkerson is fast, and Dinic is super fast
You need a lot of experience
If you can't solve with Dinic, that is not a flow problem

I'm not sure it is a good practice. If you are sure that is not a good practice, please update this article.

→ Reply

8 years ago, # ^ |

+23

In case of unit capacity Dinic works in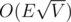 $\text{[math]}$

→ Reply

8 years ago, # ^ |

+13

I'm aware of proof for O(EV^2 / 3) but I never heard of faster one. Can I ask about some resources for it?

→ Reply

8 years ago, # ^ |

+13

I don't remember where I have seen it. Proof looks very likely to the proof of Hoproft-Carp maximal matching algorithm.

→ Reply

8 years ago, # ^ |

+10

You can find it on e-maxx.ru

→ Reply

c175353

8 years ago, # ^ |

Would you spell it out a bit more?

The "special cases" section in https://en.wikipedia.org/wiki/Dinic%27s_algorithm gives that running time only for bipartite matching.

→ Reply

tehqin

8 years ago, # ^ |

+26

That runtime needs the additional requirement of in degree 1 or out degree 1 for each node. The bipartite matching case meets this requirement.

→ Reply

8 years ago, # ^ |

+28

At first, I accidently gave one downvote to this reply. Does that explains it's -15 downvote?

→ Reply

Edvard

8 years ago, # ^ |

Here 3053014 is the push preflow algorithm implementation that is faster than Dinic (for the given problem), so Dinic not always the fastest flow algorithm.

→ Reply

8 years ago, # ^ |

+10

I was (and probably, they were) aware of push flow algo for maxflow. I just wanted to stress out that the problemsetter don't usually force it, even though there might be a case that I want to force my non-model flow sln to pass.

→ Reply

Edvard

8 years ago, # |

How to solve E?

→ Reply

8 years ago, # ^ |

+69

Add X to the cost of each edge that connects a special vertex and a non-special vertex, and find an MST in this graph.

If you are lucky and this MST contains exactly k edges between special vertices and non-special vertices, this is the answer.

Otherwise you should change the value of X to be "lucky" — do binary search on X.

→ Reply

ifsmirnov

8 years ago, # ^ |

+18

Why does there exist such X that the MST contains exactly k edges? We had this solution accepted, though we had to consider carefully the cases where we can add either special or non-special edge to the MST.

→ Reply

8 years ago, # ^ |

+16

That is a truly amazing solution. Is there any other solution that ordinary people can think?

→ Reply

BhaskarTM

4 years ago, # ^ |

How can we prove that the k edges obtained in this process would correspond to the final answer?

→ Reply

Um_nik

8 years ago, # ^ |

+20

Take complete graph, all edges have weight 1, k is somewhere in the middle.

→ Reply

http://codeforces.net/contest/125/status/E

8 years ago, # ^ |

+15

More precisely, for a fixed X, I computed L_X and R_X — the minimum/maximum possible number of special edges in an MST. Then L_X + 1 = R_X.

→ Reply

Um_nik

8 years ago, # ^ |

I believe if x is double
Still not obvious how to restore the answer

→ Reply

skydog

8 years ago, # ^ |

← Rev. 4 →

Probably one can think in this way. Let the answer tree be T and its cost to be C. Suppose when you add weight x to each special edge, you can construct an MST T' with k special edges, and the cost of T' is C'.

(1) If we subtract weight x for each special edge of T', we still get a spanning tree with cost C'- k*x.By the property of our answer tree, C <= C'- k*x.

(2) If we add x for each special edge of T, we get a spanning tree with cost C + k*x. Then by the property of T', we have C' <= C + k*x.

(3) By (1) and (2), C = C'-k*x.

So if we can find such an x to we can construct an MST with k special edges, we can simply output C'-k*x, and no solution otherwise? (not sure)

→ Reply

pavel.savchenkov

8 years ago, # ^ |

← Rev. 3 →

+35

It sufficient to consider only integer x because sorting of edges by weight changes only in integer points. To get L_x in case of equal weights we prefer usual edges, opposite for R_x. If x is increased by 1, then all special edges jump to next weight and order of edges in R_x and L_x + 1 will be the same.
To get spanning tree with L_x ≤ k ≤ R_x edges, we can consider intervals of edges with equal weights independently (because for prefix of edges we will always get the same set of components regardless of their order in Kruskal's algorithm). To get spanning tree with any possible number of special edges one can build components using only usual edges, then add all necessary special edges (there are L_x of them), then add any subset of spanning tree on remaining special edges.

→ Reply

lmn0x4F

8 years ago, # ^ |

+10

black magic

→ Reply

mkirsche

8 years ago, # ^ |

+22

→ Reply

Edvard

8 years ago, # ^ |

I have been solving that problem maybe 4 years ago and already forgotten about it :(

→ Reply

Timur_Sitdikov

8 years ago, # |

How to solve D?

→ Reply

ifsmirnov

8 years ago, # ^ |

← Rev. 3 →

+16

DP on subtrees with merging sets. First, make all numbers different. Let d(x) be the answer at some subtree if all taken vertices have value ≤ x. We store in a set all such x that d(x) ≠ d(x - 1) (note that in this case d(x) = d(x - 1) + 1).

Now if you look at the transition formulas (or stare at the values of these sets on some examples) you will see that the recalculation is similar to finding the LIS. First, we merge the sets of the children. Second, we replace the value set.upper_bound(w_v) with the value w_v or add it to the set if upper bound does not exist. The answer is the size of the set in the root.

Honestly, I don't know how to come up with this solution without staring at the examples.

→ Reply

8 years ago, # ^ |

+64

For motivation, you can notice is if the tree is a line graph, then this is exactly computing LIS on the sequence. Anyways, here's a short implementation of the above approach:

code

#include <bits/stdc++.h>

#define all(c) c.begin(),c.end()

using namespace std;

const int MAXN = 200010;

int n, p[MAXN], v[MAXN], x[MAXN];
multiset<int> s[MAXN];

int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
		scanf("%d%d", v+i, p+i);
		x[i] = i;
	}

	for (int i = n; i >= 1; i--) {
		auto it = s[x[i]].upper_bound(v[i]-1);
		if (it != s[x[i]].end()) s[x[i]].erase(it);
		s[x[i]].insert(v[i]);
		if (s[x[i]].size() < s[x[p[i]]].size()) {
			s[x[p[i]]].insert(all(s[x[i]]));
		} else {
			s[x[i]].insert(all(s[x[p[i]]]));
			x[p[i]] = x[i];
		}
	}

	printf("%d\n", (int)s[x[0]].size());
}

→ Reply

soul_voyage

6 years ago, # ^ |

Can you share some similar problems

→ Reply

rsFalse

8 years ago, # |

+11

How to solve A?

→ Reply

rajat1603

8 years ago, # ^ |

Sort all bracket sequences according to some weird combination of minimum depth and sum , then do DP.

→ Reply

arknave

8 years ago, # ^ |

We got this by just trying several sort functions. Is there intuition for why this one is correct?

→ Reply

8 years ago, # ^ |

You can mention some combination?

→ Reply

8 years ago, # ^ |

You can mention any?

→ Reply

rajat1603

8 years ago, # ^ |

← Rev. 2 →

pre = minimum prefix sum
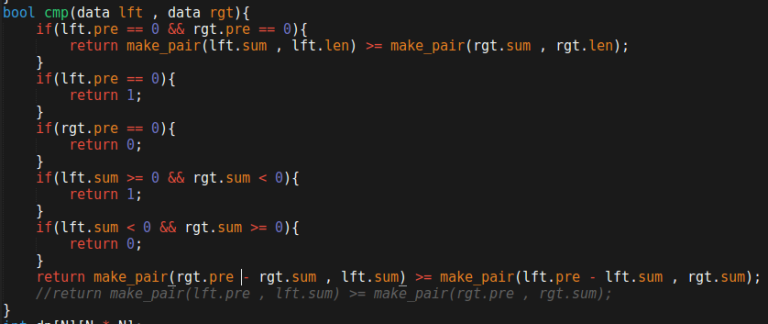
len = length of bracket
sum = sum ( = +1 and ) = -1

Note that i am not sure why it worked , i tried several combinations until i got ac.

→ Reply

animeshf

8 years ago, # ^ |

← Rev. 2 →

I tried to find a specific combination for around 2 hours in the contest, got super frustrated, wrote several comparators and ran the DP against them all, and printed the maximum answer (AC). Wasted almost entire contest on A :/

→ Reply

8 years ago, # ^ |

my team solve the problem in the contest with similar idea
this is a more deep analysis

The main idea is that if some comparator can be defined so that,
if the pieces are previously sorted, always exist some optimal solution 
that can be formed following this order, 
then doing basic dp we arrive at the solution

The same notation:
pre = minimum prefix sum
len = length of bracken
sum = sum ( = +1 and ) = -1

Note that we can ignore the couples of open-closed parentheses(without change the len property) for one more clear view, this do not change any thing, then exist three types of pieces
 
1 - Open Type
    (())(( --------> is ((
    ((()( ---------> is (((
    pre >= 0

2 - Closed-Open Type
    ()))()( -------> is ))(
    ))))(())())(()(---> is )))))((
    pre < 0 && pre != sum

3 - Closed Type
    )))())---------> is )))))
    ()()()())))----> is )))
    pre < 0 && pre == sum

The Closed-Open Type has two subtypes:

2.1 - Incremental Closed-Open ( more open parentheses that closed parentheses )
      ))()())(((( -----> is )))((((
      )()(((((((( -----> is )((((((((
      pre < 0 && pre != sum && sum >= 0

2.2 - Decremental Closed-Open ( more closed parentheses that open parentheses )
      ))()())(( -----> is )))((
      ))()( -----> is ))(
      pre < 0 && pre != sum && sum < 0

Any correct sequence of pieces can be reorder in this way: 
first --------> open pieces ( in any order )
next  --------> incremental-closed-open pieces ( in decreasing order of pre ) 
next  --------> decremental-closed-open pieces ( NOT exist any correct comparator ) 
and finally --> closed pieces ( in any order )  
and the sequence remains correct

But the issue is that NOT exist any correct comparator for decremental-closed-open pieces, many teams, my team included, accepted this problem with wrong criteries for compare decremental-closed-open pieces,
for example:
- decreasing order of pre (My solution)
- decreasing order of par(pre - sum , sum)
Both criteries has WRONG SOLUTION to this case:
4
(((((
))))(
)))))((((
)

The correct idea is that if we have a good way of compare open and incremental-closed-open pieces, then we can divide the problem in two parts: 
1 - for each possible value v, what is the maximum lentgh of any sequence formed using only open and incremental-closed-open pieces, with exactly v open parentheses without couple, this problem can be solved sorting open and incremental-closed-open pieces and doing dp

2 - for each possible value v, what is the maximum lentgh of any sequence formed using only decremental-closed-open and closed pieces, with exactly v closed parentheses without couple, this problem is similar to 1 if the pieces are reverted and the parentheses are changed '('-->')' and ')'-->'('.

Now the solution for original problem would be
Max( dp[v] + dp2[v] ) for all possible value v

→ Reply

skydog

8 years ago, # ^ |

+10

→ Reply

8 years ago, # |

How to solve B?

→ Reply

Ioana

8 years ago, # ^ |

+10

Once you know the plane where one of the bases is, you can project all the points on it, and the result will be the maximum distance to that plane (height of the cylinder) * area of minimum circle that covers the projected points (a 2D problem for which there is a randomized algorithm with expected runtime O(N) ).

The problem is finding those planes, since it takes too long to check all the candidates, even with the information that there are at least 3 points on one of the bases. I've tried all sorts of tricks and randomized checkers and failed during the contest, and the only way I could get accepted afterwards was with 3d Convex Hull (the planes we are looking for will be the planes of the hull faces which I'm pretty sure are at most O(N)).

I'm really curious if others got it without Convex Hull.

→ Reply

8 years ago, # ^ |

+10

You need to do 3d convex hull, then apply steps above. The 3d convex hull is made slightly easier by the fact that you can do it in O(n^2).

For instance, here's my code for 3d convex hull using gift wrapping (~10-15 lines).

gift wrapping

        // call dfs(i,j), where i,j is any edge on convex hull, and this will visit all faces
        void dfs(int i, int j) {
            if (vis[i][j]) return;
            vis[i][j] = true;

            int k = 0;
            while (k == i || k == j) k++;
            for (int l = 0; l < n; l++) {
                // side returns which side pts[l] lies on plane defined by pts[i],pts[j],pts[k].
                if (l != i && l != j && side(pts[i], pts[j], pts[k], pts[l]) > 0)
                    k = l;
            }
            // points i,j,k form a face on convex hull.
            ans = min(ans, getVolume(i, j, k));
            dfs(k, j);
            dfs(i, k);
        }

→ Reply

Swistakk

8 years ago, # ^ |

← Rev. 2 →

+10

That's a nice idea, but how do you find any edge from convex hull?

We used incremental approach to find convex hull, it's also fine (add vertices one by one and update faces).

→ Reply

8 years ago, # ^ |

+10

You can project it to the xy plane and find an edge of the convex hull there. For example, ignore z coordinates and take the lowermost leftmost point, the crossing most clockwise point will give you an edge on the convex hull. Someone else also had an incremental hill solution that was pretty short. It also has the added advantage of handling four colplanar points more robustly.

→ Reply

King_of_Snus

5 years ago, # ^ |

sorry for necrobloging but why this solution will find all faces?

→ Reply