| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
Here's the tutorial. Code can be found in this link (more will be added there soon): https://www.dropbox.com/sh/xwxn3zrl1icp3i2/AACtYSdYH0KlTEdVgCFFgPrYa?dl=0
Hello again Codeforces!
The Forethought Future Cup Final round will start on May 4th, 10:05am PDT. This round will be rated for everyone. There will be three separate rounds, one for onsite contestants, one for div1, and one for div2. Onsite and div1 will have the same problems. Each round will have 6 problems and be 2 hours long.
Here is a table of the onsite contestants.
The onsite round has cash prizes:
- 1st: $500
- 2nd: $250
- 3rd: $100
- 4th — 10th: $50
Thanks to ismagilov.code, mohammedehab2002, Jeel_Vaishnav, Learner99, 300iq, dojiboy9, vlyubin, y0105w49, KAN, arsijo for testing and coordination. Also, thanks to cyand1317 for one of the problems. Of course, thanks to MikeMirzayanov for Codeforces and Polygon, and for allowing us to host the round.
There might be some interactive problems again, so please read the interactive problem guide if you haven't before.
If you're still interested in applying, please fill out the form.
Updates
UPD 1 The scoring distribution will be:
- Div2: 500-1000-1500-2000-2500-3000
- Div1: 500-1000-1500-2000-2500-3250
UPD 2 Pictures from the onsite round: https://codeforces.net/blog/entry/66876
UPD 3: I'm sorry, but to prevent the leak of onsite results, we will postpone the start of system testing a bit. As soon as the closing ceremony finish at Forethought office, we will immediately start the system testing of the rounds. Until this time, the rounds will be hidden. But don't panic, this will only be temporary and we will return everything soon.
UPD 4: The results will be in around 90 minutes after the end of the competition.
UPD 5: Tutorial: https://codeforces.net/blog/entry/66878
UPD 6: Congratulations to the winners:
Onsite contest:
| 1 | scott_wu |
| 2 | ACRush |
| 3 | neal |
| 4 | xiaowuc1 |
| 5 | Svlad_Cjelli |
| 6 | Ra16bit |
| 7 | ll931110 |
| 8 | stevenkplus |
| 9 | yzyz |
| 10 | pmnox |
Div 1 contest:
| 1 | Benq |
| 2 | Petr |
| 3 | Errichto |
| 4 | aid |
| 5 | Endagorion |
Div 2 contest:
| 1 | Ezys |
| 2 | nitishk24 |
| 3 | gonP |
| 4 | trabbbart |
| 5 | EvgeniyZh |
I wrote a post about coming up with problem ideas here with some examples: https://www.topcoder.com/blog/how-to-come-up-with-problem-ideas/
Here's the tutorial. Code can be found in this link: https://www.dropbox.com/sh/wfr12qqhcrdwwlv/AAAgg-7NcqRHIysVjHvmcR_Ta?dl=0
First solve: tourist, 00:00:50
First solve: tourist, 00:02:37
First solve: tourist, 00:05:09
First solve: tourist, 00:12:53
First solve: tourist, 00:27:19
First solve: fivedemands, 00:16:00
First solve: 300iq, 00:24:05
First solve: snuke at 00:59:44
Hi Codeforces!
I'm excited to announce the Forethought Future Cup! It will consist of two rounds, an online round on April 20th, 11:05am PDT, and an onsite round on May 4th, 10:05am PDT. Both of these rounds will be rated and open for all participants. The top 25 local contestants near San Francisco will be invited to the Forethought office to take part onsite.
Each round will be a combined round. In the first round, there will be 8 problems in 2.5 hours. There will be at least one interactive problem in this round. Please read the interactive problem guide if you haven’t already.
The problems in this round were all written by me. Thanks to ismagilov.code, mohammedehab2002, Jeel_Vaishnav, Learner99, dojiboy9, vlyubin, y0105w49, KAN, arsijo for testing and coordination. Of course, thanks to MikeMirzayanov for Codeforces and Polygon, and for allowing us to host the round.
Prizes
T-shirts will be awarded to all onsite participants. 25 shirts will also be randomly awarded to contestants in the elimination round with ranks 1 to 250. The onsite round will also have some monetary prizes:
- First: $500
- Second: $250
- Third: $100
- 4th — 10th: $50
About Forethought:
At Forethought, our mission is to use AI technology to augment human abilities and make everyone “a genius at their job”. Our main product is Agatha, an assistant that helps customer support agents answer cases more quickly and confidently by suggesting answers and triaging cases. We've raised over $10M in VC funding and were the winners of 2018 SF TechCrunch Disrupt Battlefield.
I joined Forethought back in December 2018. We are a small 12 person startup, and have a lot of competitive programmers on our team, including me, y0105w49, vlyubin, and dojiboy9 (our CEO, who is also an ICPC World Finals Judge). I’m happy to answer any questions about working here in the comments below or through PM.
We’re hiring! Please fill out this form if you are interested.
Updates
UPD 1 The scoring distribution will be 500-1000-1500-2250-2500-3250-3250-3750
UPD 2 Tutorial can be found here: https://codeforces.net/blog/entry/66639
UPD 3 Congratulations to the top 5!
NAIPC is happening again on March 2nd (start time). Information about the contest can be found on this page. Information about registering can be found on here. You can register in teams of up to 3. The deadline for registration is February 28th. This contest will be hosted on Kattis again.
A few hours later, it will be available as an open cup round as the Grand Prix of America (start time). Please participate in only one of them, and don't discuss problems here until after the open cup round has ended.
You can see some past years' problems here: 2018, 2017
UPD 1: Registration is ending soon.
UPD 2: Please don't discuss until after open cup is over.
UPD 3: You can find test data and solutions here: http://serjudging.vanb.org/?p=1349
Recently, I wrote about my experiences with problem writing. This was something I haven't really talked about, and I felt it was time to share.
Read here: https://www.topcoder.com/blog/a-problem-writing-journey/
Feel free to leave comments or questions!
I'm not sure I've seen a post about this yet. Topcoder has posted their schedule for online rounds for TCO here: http://tco18.topcoder.com/algorithm/schedule/
It seems the round structure also seems to have changed. The rounds are 1A,1B, 2A,2B, 3A,3B, and a single round 4. Round 4 feeds directly into the onsite, with 14 finalists (and also 2 from a wildcard round, for a total of 16, 4 more from last year).
NAIPC is coming up on March 24th (start time here). More information about the contest can be found on this page. More information on how to register can be found on this page. You can register in teams of up to 3. This contest will be on Kattis.
Several hours later, it will be available as an open cup round as the Grand Prix of America (start time here). Please only participate in one of them, and don't discuss problems here until after the open cup round has ended.
The deadline to register for the contest on Kattis is March 21st. You will need an ICPC account to register (you can see instructions in the link above on how to create one if needed).
You can see some past years' problems here: 2017, 2016
UPD 1: The deadline to register your team is soon.
UPD 2: Contests are over
- NAIPC standings: https://naipc18.kattis.com/standings
- open cup standings: http://opentrains.snarknews.info/~ejudge/res/res10416
- solutions and test data: http://serjudging.vanb.org/?p=1165
First, let's try to find the largest block that two patrols can cover (hint, it's not k). For instance, we can have one patrol cover 1, 2, ..., k. and the other cover 2, 3, ..., k + 1.
So, we can split n houses into blocks of length k + 1. Now, we have to look at what to do with the leftover houses. If there are more than two empty blocks, we need two patrols to cover both blocks. If there is only one empty block, we only need one patrol. Thus, the answer can be computed by the formula in the code below
n,k = map(int, raw_input().split())
print (n/(k+1))*2 + min(2, n%(k+1))
We can check that this is equivalent to counting the number of permutations of 0, 1, 2, ..., 9 that appear in s.
There are two solutions:
Just do it. This is O(10! * |s|) ~ 3*10^8. This is fast enough in some languages.
#include <bits/stdc++.h>
using namespace std;
#define forn(i, n) for (int i = 0; i < (int)(n); ++i)
#define fore(i, b, e) for (int i = (int)(b); i <= (int)(e); ++i)
#define ford(i, n) for (int i = (int)(n) - 1; i >= 0; --i)
#define pb push_back
#define fi first
#define se second
#define all(x) (x).begin(), (x).end()
typedef vector<int> vi;
typedef pair<int, int> pii;
typedef long long i64;
typedef unsigned long long u64;
typedef long double ld;
typedef long long ll;
const int maxn = 105;
int n;
int a[maxn];
int p[maxn];
bool check() {
int cur = 0;
forn(i, n) {
if (p[a[i]] == cur) ++cur;
}
return cur == 10;
}
int main() {
#ifdef LOCAL
freopen("b.in", "r", stdin);
#endif
char c;
while (cin >> c) { a[n++] = c-'0'; }
forn(i, 10) p[i] = i;
int cnt = 0;
do {
cnt += check();
} while (next_permutation(p, p+10));
cout << cnt << endl;
#ifdef LOCAL
cerr << "Time elapsed: " << clock() / 1000 << " ms" << endl;
#endif
return 0;
}
We can do a bitmask dp. We need to be careful not to double count, so we advance our index to the first occurence of some character to take it. See the code for more details.
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
const int N = 105;
vector<int> pos[N];
char buf[N];
const int MSK = 1 << 10;
int D[MSK][N];
const int K = 10;
int main() {
scanf("%s", buf);
int n = strlen(buf);
for (int i = 0; i < n; i++) {
pos[buf[i] - '0'].push_back(i);
}
D[0][0] = 1;
for (int msk = 0; msk < MSK - 1; msk++) {
for (int i = 0; i < K; i++) {
if ((msk >> i) & 1) {
continue;
}
for (int j = 0; j <= n + 1; j++) {
if (j == n + 1) {
D[msk | (1 << i)][j] += D[msk][j];
} else {
int p = lower_bound(pos[i].begin(), pos[i].end(), j) - pos[i].begin();
if (p == pos[i].size()) {
p = n + 1;
} else {
p = pos[i][p];
}
D[msk | (1 << i)][p + 1] += D[msk][j];
}
}
}
}
int ans = 0;
for (int i = 0; i <= n; i++) {
ans += D[MSK - 1][i];
}
printf("%d\n", ans);
}
Consider at each step, instead of adding our score to a global counter, we incremented the score at a particular vertex. So, we only need to simulate one round, and can multiply by an appropriate constant to get the limit value. We can also check the infinite case here (the contribution of a node is nonzero and it never gets chosen so its value never gets reduced).
The problem is that this approach takes O(nk) time in the worst case. Let's look at each edge individually. If node a appears fa times, and node b appears fb times in our sequence, we can get the contribution of this edge onto each node's values in O(fa + fb) time. We can also further reduce this to O(min(fa, fb) * log(max(fa, fb))) time by iterating through the explicit occurences of the node that appears fewer times, and using some data structures to count the number of occurences of the other node between any two explicit occurences.
With this reduction, this brings our running time to O(n * sqrt(n) * log(n)) (for example, see this problem for analysis: http://codeforces.net/problemset/problem/804/D)
#include <cstdio>
#include <cassert>
#include <cstdlib>
#include <vector>
using namespace std;
const int MOD = 1000 * 1000 * 1000 + 7;
inline int add(int a, int b) {
if ((a += b) >= MOD) {
a -= MOD;
}
return a;
}
typedef long long llong;
inline int mul(int a, int b) {
return ((llong)a) * b % MOD;
}
inline int sub(int a, int b) {
if ((a -= b) < 0) {
a += MOD;
}
return a;
}
int powmod(int a, int b) {
int res = 1;
while (b > 0) {
if (b & 1) {
res = mul(res, a);
}
a = mul(a, a);
b >>= 1;
}
return res;
}
int inv(int x) {
return powmod(x, MOD - 2);
}
const int N = 100500;
int V[N];
vector<int> history[N];
int AF[N];
void die() {
puts("-1");
exit(0);
}
int pw2[N];
int main() {
int n, m, k;
scanf("%d %d %d", &n, &m, &k);
for (int i = 0; i < n; i++) {
scanf("%d", &V[i]);
}
for (int i = 0; i < k; i++) {
int s;
scanf("%d", &s);
--s;
history[s].push_back(i);
}
pw2[0] = 1;
for (int i = 0; i < k; i++) {
pw2[i + 1] = (pw2[i] % 2 == 0) ? pw2[i] / 2 : (pw2[i] + MOD) / 2;
}
for (int i = 0; i < m; i++) {
int a, b;
scanf("%d %d", &a, &b);
--a, --b;
if (history[a].size() > history[b].size()) {
swap(a, b);
}
if (history[b].empty()) {
continue;
} else if (history[a].empty()) {
if (V[a] == 0) {
continue;
} else {
die();
}
} else {
int prv = 0;
for (int i = 0; i < (int)history[a].size(); i++) {
int x = history[a][i];
int p = lower_bound(history[b].begin(), history[b].end(), x) - history[b].begin();
AF[b] = add(AF[b], pw2[p]);
AF[a] = add(AF[a], mul(p - prv, pw2[i]));
prv = p;
}
AF[a] = add(AF[a], mul((int)history[b].size() - prv, pw2[(int)history[a].size()]));
}
}
int ans = 0;
for (int i = 0; i < n; i++) {
if (AF[i] != 0) {
assert(!history[i].empty());
}
int k = pw2[(int)history[i].size()];
int num = mul(AF[i], V[i]);
int den = sub(1, k);
ans = add(ans, mul(num, inv(den)));
}
printf("%d\n", ans);
}
import java.io.OutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.util.stream.Stream;
import java.io.BufferedWriter;
import java.io.Writer;
import java.io.OutputStreamWriter;
import java.util.InputMismatchException;
import java.io.IOException;
import java.util.Collections;
import java.util.ArrayList;
import java.io.InputStream;
/**
* Built using CHelper plug-in
* Actual solution is at the top
*/
public class Main {
public static void main(String[] args) {
InputStream inputStream = System.in;
OutputStream outputStream = System.out;
InputReader in = new InputReader(inputStream);
OutputWriter out = new OutputWriter(outputStream);
InfiniteGraphGame solver = new InfiniteGraphGame();
solver.solve(1, in, out);
out.close();
}
static class InfiniteGraphGame {
public int mod = 1000000007;
int[] cc;
int[] sz;
ArrayList<Integer>[] pos;
public void solve(int testNumber, InputReader in, OutputWriter out) {
int n = in.nextInt(), m = in.nextInt(), k = in.nextInt();
int[] v = in.readIntArray(n);
int[] s = in.readIntArray(k);
for (int i = 0; i < k; i++) s[i]--;
pos = Stream.generate(ArrayList::new).limit(n).toArray(ArrayList[]::new);
for (int i = 0; i < n; i++) pos[i].add(0);
cc = new int[k + 1];
sz = new int[n];
for (int i = 1; i <= k; i++) {
cc[i] = pos[s[i - 1]].size();
pos[s[i - 1]].add(i);
sz[s[i - 1]]++;
}
long[] div2 = new long[k + 1];
div2[0] = 1;
long mult = Utils.inv(2, mod);
for (int i = 1; i < div2.length; i++) {
div2[i] = div2[i - 1] * mult % mod;
}
long ans = 0;
for (int i = 0; i < m; i++) {
int a = in.nextInt() - 1, b = in.nextInt() - 1;
if (sz[a] > sz[b]) {
int t = a;
a = b;
b = t;
}
if (sz[b] > 0 && sz[a] == 0 && v[a] > 0) {
out.println(-1);
return;
}
long sa = 0, sb = 0;
int da = 0, db = 0;
int lastw = 0;
for (int q : pos[a]) {
if (q == 0) continue;
int curw = cc[pos[b].get(-Collections.binarySearch(pos[b], q) - 2)];
long w = curw - lastw;
lastw = curw;
sa = (sa + 1L * w * v[a] % mod * div2[da]) % mod;
db += w;
sb = (sb + v[b] * div2[db]) % mod;
da++;
}
{
long w = sz[b] - lastw;
sa = (sa + 1L * w * v[a] % mod * div2[da]) % mod;
db += w;
}
sa = sa * Utils.inv(1 - div2[da] + mod, mod) % mod;
sb = sb * Utils.inv(1 - div2[db] + mod, mod) % mod;
ans = (ans + sa + sb) % mod;
}
out.println(ans);
}
}
static class OutputWriter {
private final PrintWriter writer;
public OutputWriter(OutputStream outputStream) {
writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(outputStream)));
}
public OutputWriter(Writer writer) {
this.writer = new PrintWriter(writer);
}
public void close() {
writer.close();
}
public void println(long i) {
writer.println(i);
}
public void println(int i) {
writer.println(i);
}
}
static class InputReader {
private InputStream stream;
private byte[] buf = new byte[1 << 16];
private int curChar;
private int numChars;
public InputReader(InputStream stream) {
this.stream = stream;
}
public int[] readIntArray(int tokens) {
int[] ret = new int[tokens];
for (int i = 0; i < tokens; i++) {
ret[i] = nextInt();
}
return ret;
}
public int read() {
if (this.numChars == -1) {
throw new InputMismatchException();
} else {
if (this.curChar >= this.numChars) {
this.curChar = 0;
try {
this.numChars = this.stream.read(this.buf);
} catch (IOException var2) {
throw new InputMismatchException();
}
if (this.numChars <= 0) {
return -1;
}
}
return this.buf[this.curChar++];
}
}
public int nextInt() {
int c;
for (c = this.read(); isSpaceChar(c); c = this.read()) {
;
}
byte sgn = 1;
if (c == 45) {
sgn = -1;
c = this.read();
}
int res = 0;
while (c >= 48 && c <= 57) {
res *= 10;
res += c - 48;
c = this.read();
if (isSpaceChar(c)) {
return res * sgn;
}
}
throw new InputMismatchException();
}
public static boolean isSpaceChar(int c) {
return c == 32 || c == 10 || c == 13 || c == 9 || c == -1;
}
}
static class Utils {
public static long inv(long N, long M) {
long x = 0, lastx = 1, y = 1, lasty = 0, q, t, a = N, b = M;
while (b != 0) {
q = a / b;
t = a % b;
a = b;
b = t;
t = x;
x = lastx - q * x;
lastx = t;
t = y;
y = lasty - q * y;
lasty = t;
}
return (lastx + M) % M;
}
}
}
The bounds might look a bit strange, and it was a bit hard to find good bounds for this. Originally, I wanted to set bounds higher so only O(n3·logn) solutions could pass, but it seems the constant factor for that solution is too high. So, I set bounds low enough so a O(n4) solution could pass as well.
For an O(n4) solution, we can check all O(n^2) substrings. Now, we want to know if this string can stamp out the entire string. We can do this with dp. Let dp[i][j] be true if it is possible to stamp out the prefix 1, ..., i with (j + 1, ..., m) possibly left over the right edge. You can see the code below on how to update the dp table. This takes O(m^2) time per string so overall runtime is O(n^4) with a fairly low constant. We can get some more constant factor optimizations by doing some early breaks.
#ifdef LOCAL
#define _GLIBCXX_DEBUG
#endif
#include <bits/stdc++.h>
using namespace std;
#define forn(i, n) for (int i = 0; i < (int)(n); ++i)
#define fore(i, b, e) for (int i = (int)(b); i <= (int)(e); ++i)
#define ford(i, n) for (int i = (int)(n) - 1; i >= 0; --i)
#define pb push_back
#define fi first
#define se second
#define all(x) (x).begin(), (x).end()
typedef vector<int> vi;
typedef pair<int, int> pii;
typedef long long i64;
typedef unsigned long long u64;
typedef long double ld;
typedef long long ll;
const int maxn = 500;
int n, m;
string s;
string t;
char d[maxn][maxn];
void scan() {
cin >> s;
n = s.size();
}
bool check() {
memset(d, 0, sizeof d);
m = t.size();
if (s[0] != t[0]) return false;
d[1][1] = 1;
fore(i, 2, n) fore(j, 1, m) if (t[j-1] == s[i-1]) {
if (d[i-1][j-1]) d[i][j] = 1;
if (d[i-1][m]) d[i][j] = 1;
if (j == 1) fore(k, 1, m-1) if (d[i-1][k]) { d[i][j] = 1; break; }
}
return d[n][m];
}
void solve() {
set<string> res;
set<string> seen;
forn(i, n) forn(len, n-i+1) if (len) {
t = s.substr(i, len);
if (seen.count(t)) continue;
seen.insert(t);
if (check()) res.insert(t);
}
for (auto s: res) {
cout << s << "\n";
}
}
int main() {
#ifdef LOCAL
freopen("e.in", "r", stdin);
#endif
scan();
solve();
#ifdef LOCAL
cerr << "Time elapsed: " << clock() / 1000 << " ms" << endl;
#endif
return 0;
}
For an O(n3·logn) solution, consider all occurences of t in s (these can be found in O(|s| + |t|) time). Then, consider extending a region as far as we can left by prepending a prefix of t, and extending a region as far as we can to the right by appending a suffix of t. This can be done with a stack or segment trees. Then, we have a set of intervals, and we want to check it covers 1, ..., n. This can also be done in time after sorting. Note, there is some tricky case in that if there can be gaps between the intervals, but these gaps need to consist of substrings of t. This can also be checked in linear time using suffix automaton.
import java.io.OutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.util.Arrays;
import java.io.BufferedWriter;
import java.util.InputMismatchException;
import java.io.IOException;
import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;
import java.io.Writer;
import java.io.OutputStreamWriter;
import java.util.Collections;
import java.io.InputStream;
/**
* Built using CHelper plug-in
* Actual solution is at the top
*/
public class Main2 {
public static void main(String[] args) {
InputStream inputStream = System.in;
OutputStream outputStream = System.out;
InputReader in = new InputReader(inputStream);
OutputWriter out = new OutputWriter(outputStream);
StampStampStamp solver = new StampStampStamp();
solver.solve(1, in, out);
out.close();
}
static class StampStampStamp {
String s;
SegmentTreeFast st;
int[] r1;
int[] r2;
int[] left;
int[] right;
Pair<Integer, Integer>[] pp;
public void solve(int testNumber, InputReader in, OutputWriter out) {
s = in.next();
int n = s.length();
r1 = new int[n];
r2 = new int[n];
left = new int[n];
right = new int[n];
st = new SegmentTreeFast(n);
pp = new Pair[n];
HashSet<String> ss = new HashSet<>();
HashSet<String> t = new HashSet<>();
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
String test = s.substring(i, j + 1);
if (t.add(test) && ok(test, s)) {
ss.add(test);
}
}
}
ArrayList<String> ans = new ArrayList<>(ss);
Collections.sort(ans);
for (String x : ans) out.println(x);
}
boolean ok(String sub, String all) {
if (sub.charAt(0) != all.charAt(0) || sub.charAt(sub.length() - 1) != all.charAt(all.length() - 1))
return false;
HashSet<Character> tt = new HashSet<>();
for (char k : sub.toCharArray()) tt.add(k);
for (char k : all.toCharArray()) if (!tt.contains(k)) return false;
char[] c1 = (sub + "*" + all).toCharArray();
int[] z1 = ZAlgorithm.zAlgorithm(c1);
char[] c2 = (new StringBuffer(sub).reverse().toString() + "*" +
new StringBuffer(all).reverse().toString()).toCharArray();
int[] z2 = ZAlgorithm.zAlgorithm(c2);
int m = sub.length();
int n = all.length();
st.clear();
for (int i = n - 1; i >= 0; i--) {
int z = z1[i + m + 1];
if (z == 0) {
r1[i] = -1;
} else {
r1[i] = Math.max(i + z - 1, st.query(i + 1, i + z));
}
st.modify(i, i, r1[i]);
pp[i] = new Pair(-r1[i], i);
}
Arrays.sort(pp);
int idx = 0;
int min = n;
for (int i = n - 1; i >= 0; i--) {
while (idx < n && -pp[idx].u >= i) {
min = Math.min(min, pp[idx].v);
idx++;
}
left[i] = Math.min(min, i + 1);
}
st.clear();
int[] right = new int[n];
for (int i = 0; i < n; i++) {
int z = z2[n - i - 1 + m + 1];
if (z == 0) {
r2[i] = n + 1;
} else {
r2[i] = Math.min(i - z + 1, -st.query(i - z, i - 1));
}
st.modify(i, i, -r2[i]);
pp[i] = new Pair(r2[i], i);
}
Arrays.sort(pp);
idx = 0;
int max = -1;
for (int i = 0; i < n; i++) {
while (idx < n && pp[idx].u <= i) {
max = Math.max(max, pp[idx].v);
idx++;
}
right[i] = Math.max(i - 1, max);
}
ArrayList<Integer> evts = new ArrayList<>();
for (int i = 0; i < n; i++) {
if (z1[i + m + 1] == m) {
evts.add((i == 0 ? 0 : left[i - 1]) * 2 + 0);
evts.add(right[i] * 2 + 1);
}
}
Collections.sort(evts);
SuffixAutomaton.State[] automaton = SuffixAutomaton.buildSuffixAutomaton(sub);
int psum = 0;
for (int i = 0; i + 1 < evts.size(); i++) {
int k = evts.get(i);
if (k % 2 == 0) psum++;
else psum--;
if (psum == 0) {
int cur = k / 2 + 1;
int nxt = evts.get(i + 1) / 2;
int node = 0;
for (int j = cur; j < nxt; j++) {
int next = automaton[node].next[all.charAt(j)];
if (next == -1) return false;
node = next;
}
}
}
return evts.get(0) / 2 == 0 && evts.get(evts.size() - 1) / 2 == n - 1;
}
}
static class ZAlgorithm {
public static int[] zAlgorithm(char[] let) {
int N = let.length;
int[] z = new int[N];
int L = 0, R = 0;
for (int i = 1; i < N; i++) {
if (i > R) {
L = R = i;
while (R < N && let[R - L] == let[R])
R++;
z[i] = R - L;
R--;
} else {
int k = i - L;
if (z[k] < R - i + 1)
z[i] = z[k];
else {
L = i;
while (R < N && let[R - L] == let[R])
R++;
z[i] = R - L;
R--;
}
}
}
z[0] = N;
return z;
}
}
static class OutputWriter {
private final PrintWriter writer;
public OutputWriter(OutputStream outputStream) {
writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(outputStream)));
}
public OutputWriter(Writer writer) {
this.writer = new PrintWriter(writer);
}
public void print(Object... objects) {
for (int i = 0; i < objects.length; i++) {
if (i != 0) {
writer.print(' ');
}
writer.print(objects[i]);
}
}
public void println(Object... objects) {
print(objects);
writer.println();
}
public void close() {
writer.close();
}
}
static class SuffixAutomaton {
public static SuffixAutomaton.State[] buildSuffixAutomaton(CharSequence s) {
int n = s.length();
SuffixAutomaton.State[] st = new SuffixAutomaton.State[Math.max(2, 2 * n - 1)];
st[0] = new SuffixAutomaton.State();
st[0].suffLink = -1;
int last = 0;
int size = 1;
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
int cur = size++;
st[cur] = new SuffixAutomaton.State();
st[cur].length = i + 1;
st[cur].firstPos = i;
int p = last;
for (; p != -1 && st[p].next[c] == -1; p = st[p].suffLink) {
st[p].next[c] = cur;
}
if (p == -1) {
st[cur].suffLink = 0;
} else {
int q = st[p].next[c];
if (st[p].length + 1 == st[q].length) {
st[cur].suffLink = q;
} else {
int clone = size++;
st[clone] = new SuffixAutomaton.State();
st[clone].length = st[p].length + 1;
System.arraycopy(st[q].next, 0, st[clone].next, 0, st[q].next.length);
st[clone].suffLink = st[q].suffLink;
for (; p != -1 && st[p].next[c] == q; p = st[p].suffLink) {
st[p].next[c] = clone;
}
st[q].suffLink = clone;
st[cur].suffLink = clone;
}
}
last = cur;
}
for (int i = 1; i < size; i++) {
st[st[i].suffLink].invSuffLinks.add(i);
}
return Arrays.copyOf(st, size);
}
public static class State {
public int length;
public int suffLink;
public List<Integer> invSuffLinks = new ArrayList<>(0);
public int firstPos = -1;
public int[] next = new int[128];
{
Arrays.fill(next, -1);
}
}
}
static class InputReader {
private InputStream stream;
private byte[] buf = new byte[1 << 16];
private int curChar;
private int numChars;
public InputReader(InputStream stream) {
this.stream = stream;
}
public int read() {
if (this.numChars == -1) {
throw new InputMismatchException();
} else {
if (this.curChar >= this.numChars) {
this.curChar = 0;
try {
this.numChars = this.stream.read(this.buf);
} catch (IOException var2) {
throw new InputMismatchException();
}
if (this.numChars <= 0) {
return -1;
}
}
return this.buf[this.curChar++];
}
}
public String next() {
int c;
while (isSpaceChar(c = this.read())) {
;
}
StringBuilder result = new StringBuilder();
result.appendCodePoint(c);
while (!isSpaceChar(c = this.read())) {
result.appendCodePoint(c);
}
return result.toString();
}
public static boolean isSpaceChar(int c) {
return c == 32 || c == 10 || c == 13 || c == 9 || c == -1;
}
}
static class SegmentTreeFast {
int[] value;
int[] delta;
public SegmentTreeFast(int n) {
value = new int[2 * n];
for (int i = 0; i < n; i++) {
value[i + n] = getInitValue();
}
for (int i = 2 * n - 1; i > 1; i -= 2) {
value[i >> 1] = queryOperation(value[i], value[i ^ 1]);
}
delta = new int[2 * n];
Arrays.fill(delta, getNeutralDelta());
}
public void clear() {
int n = value.length / 2;
for (int i = 0; i < n; i++) {
value[i + n] = getInitValue();
}
for (int i = 2 * n - 1; i > 1; i -= 2) {
value[i >> 1] = queryOperation(value[i], value[i ^ 1]);
}
Arrays.fill(delta, getNeutralDelta());
}
int modifyOperation(int x, int y) {
return Math.max(x, y);
}
int queryOperation(int leftValue, int rightValue) {
return Math.max(leftValue, rightValue);
}
int deltaEffectOnSegment(int delta, int segmentLength) {
if (delta == getNeutralDelta()) return getNeutralDelta();
// Here you must write a fast equivalent of following slow code:
// int result = delta;
// for (int i = 1; i < segmentLength; i++) result = queryOperation(result, delta);
// return result;
return delta;
// return delta * segmentLength;
}
int getNeutralDelta() {
return -(1 << 29);
}
int getInitValue() {
return -(1 << 29);
}
int joinValueWithDelta(int value, int delta) {
if (delta == getNeutralDelta()) return value;
return modifyOperation(value, delta);
}
int joinDeltas(int delta1, int delta2) {
if (delta1 == getNeutralDelta()) return delta2;
if (delta2 == getNeutralDelta()) return delta1;
return modifyOperation(delta1, delta2);
}
void pushDelta(int i) {
int d = 0;
for (; (i >> d) > 0; d++) {
}
for (d -= 2; d >= 0; d--) {
int x = i >> d;
value[x >> 1] = joinNodeValueWithDelta(x >> 1, 1 << (d + 1));
delta[x] = joinDeltas(delta[x], delta[x >> 1]);
delta[x ^ 1] = joinDeltas(delta[x ^ 1], delta[x >> 1]);
delta[x >> 1] = getNeutralDelta();
}
}
int joinNodeValueWithDelta(int i, int len) {
return joinValueWithDelta(value[i], deltaEffectOnSegment(delta[i], len));
}
public int query(int from, int to) {
to = Math.min(to, value.length / 2 - 1);
from = Math.max(from, 0);
if (to < from) return getInitValue();
from += value.length >> 1;
to += value.length >> 1;
pushDelta(from);
pushDelta(to);
int res = 0;
boolean found = false;
for (int len = 1; from <= to; from = (from + 1) >> 1, to = (to - 1) >> 1, len <<= 1) {
if ((from & 1) != 0) {
res = found ? queryOperation(res, joinNodeValueWithDelta(from, len)) : joinNodeValueWithDelta(from, len);
found = true;
}
if ((to & 1) == 0) {
res = found ? queryOperation(res, joinNodeValueWithDelta(to, len)) : joinNodeValueWithDelta(to, len);
found = true;
}
}
if (!found) throw new RuntimeException();
return res;
}
public void modify(int from, int to, int delta) {
if (from > to) return;
from += value.length >> 1;
to += value.length >> 1;
pushDelta(from);
pushDelta(to);
int a = from;
int b = to;
for (; from <= to; from = (from + 1) >> 1, to = (to - 1) >> 1) {
if ((from & 1) != 0) {
this.delta[from] = joinDeltas(this.delta[from], delta);
}
if ((to & 1) == 0) {
this.delta[to] = joinDeltas(this.delta[to], delta);
}
}
for (int i = a, len = 1; i > 1; i >>= 1, len <<= 1) {
value[i >> 1] = queryOperation(joinNodeValueWithDelta(i, len), joinNodeValueWithDelta(i ^ 1, len));
}
for (int i = b, len = 1; i > 1; i >>= 1, len <<= 1) {
value[i >> 1] = queryOperation(joinNodeValueWithDelta(i, len), joinNodeValueWithDelta(i ^ 1, len));
}
}
}
static class Pair<U extends Comparable<U>, V extends Comparable<V>> implements Comparable<Pair<U, V>> {
public final U u;
public final V v;
public Pair(U u, V v) {
this.u = u;
this.v = v;
}
public int hashCode() {
return (u == null ? 0 : u.hashCode() * 31) + (v == null ? 0 : v.hashCode());
}
public boolean equals(Object o) {
if (this == o)
return true;
if (o == null || getClass() != o.getClass())
return false;
Pair<U, V> p = (Pair<U, V>) o;
return (u == null ? p.u == null : u.equals(p.u)) && (v == null ? p.v == null : v.equals(p.v));
}
public int compareTo(Pair<U, V> b) {
int cmpU = u.compareTo(b.u);
return cmpU != 0 ? cmpU : v.compareTo(b.v);
}
public String toString() {
return String.format("[Pair = (%s, %s)", u.toString(), v.toString());
}
}
}
Be careful, it is not true in general that the set of valid k forms an interval. For example, consider this case [6, 4, 4, 6]. k = 7 works, by turning the array into [1, 3, 4, 6]. k = 9 works by turning the array into [3, 4, 5, 6]. But, k = 8 doesn't work since the middle two elements will stay the same.
Our solution will eliminate intervals of k that are bad if we choose to flip or not flip certain elements. Let F(i) be the set of intervals that is bad if we flip element i, and let T(i) be the set of intervals that is bad if we don't flip element i.
For each individual element, if we choose to flip it, and this adds the inequality xi ≤ k, so this adds the bad interval [0, xi - 1] to F(i).
For a pair of adjacent indices xi, xi + 1, we can check we can check what inequalities it imposes on k if we decide to flip or not flip certain elements (you can see the code for the exact cases).
After getting these bad intervals, it suffices to try to find some point such that this point is not in F(i) or not in T(i) for all i. This can be done with a line sweep.
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <cassert>
using namespace std;
const int N = 200500;
int B[N];
int W[N];
int bad = 0;
int getbad(int i) {
return (W[2 * i] > 0 && W[2 * i + 1] > 0) ? 1 : 0;
}
void add(int i, int w) {
bad -= getbad(i / 2);
W[i] += w;
bad += getbad(i / 2);
}
struct ev {
int t;
int i;
int d;
friend bool operator <(const ev& a, const ev& b) {
return a.t < b.t;
}
};
vector<ev> evts;
const int INF = 2e9 + 42;
void add(int l, int r, int i) {
evts.emplace_back(ev{l, i, 1});
evts.emplace_back(ev{r + 1, i, -1});
}
int A[N];
void die() {
puts("-1");
exit(0);
}
int T(int x) {
return 2 * x + 1;
}
int F(int x) {
return 2 * x;
}
int main() {
int n;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &A[i]);
}
for (int i = 0; i < n; i++) {
add(0, A[i] - 1, F(i));
}
bool f = false;
for (int i = 0; i < n - 1; i++) {
int a = A[i];
int b = A[i + 1];
int s = a + b;
if (a == b) {
add(0, s, F(i + 1));
add(0, s, T(i));
add(s, INF, F(i));
add(s, INF, T(i + 1));
} else if (a > b) {
add(0, s, T(i));
add(s, INF, T(i + 1));
} else {
add(0, s, F(i + 1));
add(s, INF, F(i));
}
}
add(0, -1, 0); // touch
sort(evts.begin(), evts.end());
int goodk = -1;
for (int l = 0, r = 0; l < (int)evts.size(); l = r) {
if (evts[l].t >= INF - 2) {
break;
}
while (r < (int)evts.size() && evts[r].t == evts[l].t) {
r++;
}
for (int i = l; i < r; i++) {
add(evts[i].i, evts[i].d);
}
if (bad == 0) {
goodk = evts[l].t;
break;
}
}
printf("%d\n", goodk);
if (goodk != -1) {
assert(W[2 * n] == 0 || W[2 * n + 1] == 0);
for (int i = 0; i < n; i++) {
assert(W[2 * i] == 0 || W[2 * i + 1] == 0);
printf("%d ", (B[i] = ((W[2 * i] > 0) ? A[i] : goodk - A[i])));
}
printf("\n");
for (int i = 0; i < n - 1; i++) {
assert(B[i] < B[i + 1]);
}
for (int i = 0; i < n; i++) {
assert(B[i] >= 0);
}
}
}
There may be some exponential time solutions, which is why bounds are set a bit low, but you can also solve this in polynomial time with the matroid intersection algorithm in O(n^4). It might also be possible to solve this with some hill climbing algorithms, the idea is to try to maximize rank(W(A, B + X)) + rank(W(R - A, C - B - X)). I'll describe the matroid intersection algorithm.
The matroids here in this case are M1 = set of columns X such W(A, X) is linearly independent, and M2 = set of columns Y such that the rank of W(R - A, C - Y) is at least |R| - |A| (here, the rank is the maximum size of a subset of rows that is linearly independent).
The algorithm is similar to bipartite matching (in fact, bipartite matching is a special case of the matroid intersection algorithm). The rough steps are as follows. Let S be some set of elements that is in  . Initially S is empty. To increase the size of S, make a directed graph as follows:
. Initially S is empty. To increase the size of S, make a directed graph as follows:
- Make a node for every column in the graph. Also make a node for a "source" and a "sink".
- For simplicity, I'll refer to a node not in S as x and a node in S as y.
- For two nodes x, y, draw a directed edge from x to y if S + x - y belongs in M1.
- For two nodes x, y, draw a directed edge from x to y if S + x - y belongs in M2.
- Connect the source to x if S + x belongs in M1.
- Connect x to the sink if S + x belongs in M2.
We then find an "augmenting" path from the source to the sink, and we can xor this with our original set to get a set with one size larger (i.e. if it was in S remove it, otherwise add it).
The proof isn't too easy though, but you can google some papers about the algorithm for proof/more details (here and here).
Of course, this only deals with the unweighted case, so to add back B into consideration, we can give columns in B weight 1 and other columns with weight 0. We can adapt the algorithm above to find the maximum weight instead, and check it contains all elements of B.
import java.io.OutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.util.Arrays;
import java.io.BufferedWriter;
import java.util.InputMismatchException;
import java.io.IOException;
import java.util.TreeSet;
import java.util.ArrayList;
import java.util.List;
import java.util.stream.Stream;
import java.io.Writer;
import java.io.OutputStreamWriter;
import java.util.Comparator;
import java.io.InputStream;
/**
* Built using CHelper plug-in
* Actual solution is at the top
*/
public class Main {
public static void main(String[] args) {
InputStream inputStream = System.in;
OutputStream outputStream = System.out;
InputReader in = new InputReader(inputStream);
OutputWriter out = new OutputWriter(outputStream);
YetAnotherBinaryMatrix solver = new YetAnotherBinaryMatrix();
solver.solve(1, in, out);
out.close();
}
static class YetAnotherBinaryMatrix {
int n;
int na;
int nb;
int[][] mat;
int[] a;
int[] b;
long[] A;
long[] nA;
boolean[] ba;
boolean[] bb;
public void solve(int testNumber, InputReader in, OutputWriter out) {
n = in.nextInt();
na = in.nextInt();
nb = in.nextInt();
a = in.readIntArray(na);
b = in.readIntArray(nb);
ba = new boolean[n];
for (int x : a) ba[x - 1] = true;
bb = new boolean[n];
for (int x : b) bb[x - 1] = true;
mat = new int[n][n];
for (int i = 0; i < n; i++) {
char[] c = in.next().toCharArray();
for (int j = 0; j < n; j++)
mat[i][j] = c[j] - '0';
}
A = new long[n];
nA = new long[n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (ba[j]) A[i] = A[i] * 2 + mat[j][i];
else nA[i] = nA[i] * 2 + mat[j][i];
}
}
Basis bs = new Basis();
for (int i = 0; i < n; i++) bs.add(nA[i]);
if (bs.size < n - na) {
out.println(-1);
return;
}
boolean[] ss = new boolean[n];
while (true) {
int[] x = findPath(ss);
if (x == null) break;
for (int j : x) {
ss[j] = !ss[j];
}
}
int count = 0;
for (boolean w : ss) if (w) count++;
if (count != na) {
out.println(-1);
return;
}
count = 0;
for (int i = 0; i < n; i++) {
if (bb[i] && !ss[i]) {
out.println(-1);
return;
} else if (ss[i] && !bb[i]) {
count++;
}
}
out.println(count);
int[] ret = new int[count];
int idx = 0;
for (int i = 0; i < n; i++) if (ss[i] && !bb[i]) ret[idx++] = i + 1;
out.println(ret);
}
public boolean ok1(boolean[] ss) {
Basis bs = new Basis();
for (int j = 0; j < n; j++) {
if (ss[j]) {
if (!bs.add(A[j]))
return false;
}
}
return true;
}
public boolean ok2(boolean[] ss) {
Basis bs = new Basis();
for (int j = 0; j < n; j++) {
if (!ss[j]) {
bs.add(nA[j]);
}
}
return bs.size >= n - na;
}
public int[] findPath(boolean[] ss) {
int nnodes = n + 2;
List<Integer>[] graph = Stream.generate(ArrayList::new).limit(nnodes).toArray(List[]::new);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (!ss[i] && ss[j]) {
ss[i] = true;
ss[j] = false;
if (ok1(ss)) graph[i].add(j);
if (ok2(ss)) graph[j].add(i);
ss[i] = false;
ss[j] = true;
}
}
}
for (int i = 0; i < n; i++) {
if (!ss[i]) {
ss[i] = true;
if (ok2(ss)) graph[nnodes - 1].add(i);
if (ok1(ss)) graph[i].add(nnodes - 2);
ss[i] = false;
}
}
int[] prev = new int[nnodes];
int[] dist = new int[nnodes];
Arrays.fill(prev, -1);
Arrays.fill(dist, 1 << 25);
TreeSet<Integer> ts = new TreeSet<>(Comparator.comparingInt(x -> dist[x] * (n + 10) + x));
dist[nnodes - 1] = 0;
ts.add(nnodes - 1);
while (ts.size() > 0) {
int f = ts.pollFirst();
for (int nxt : graph[f]) {
int weight = (nxt < n ? 100 * (bb[nxt] ? -1 : 1) * (ss[nxt] ? -1 : 1) : 0) + 1;
if (dist[f] + weight < dist[nxt]) {
ts.remove(nxt);
dist[nxt] = dist[f] + weight;
prev[nxt] = f;
ts.add(nxt);
}
}
}
if (prev[nnodes - 2] == -1) return null;
int[] p = new int[nnodes];
int cur = prev[nnodes - 2];
int id = 0;
do {
p[id++] = cur;
cur = prev[cur];
} while (cur != nnodes - 1);
return Arrays.copyOf(p, id);
}
}
static class InputReader {
private InputStream stream;
private byte[] buf = new byte[1 << 16];
private int curChar;
private int numChars;
public InputReader(InputStream stream) {
this.stream = stream;
}
public int[] readIntArray(int tokens) {
int[] ret = new int[tokens];
for (int i = 0; i < tokens; i++) {
ret[i] = nextInt();
}
return ret;
}
public int read() {
if (this.numChars == -1) {
throw new InputMismatchException();
} else {
if (this.curChar >= this.numChars) {
this.curChar = 0;
try {
this.numChars = this.stream.read(this.buf);
} catch (IOException var2) {
throw new InputMismatchException();
}
if (this.numChars <= 0) {
return -1;
}
}
return this.buf[this.curChar++];
}
}
public int nextInt() {
int c;
for (c = this.read(); isSpaceChar(c); c = this.read()) {
;
}
byte sgn = 1;
if (c == 45) {
sgn = -1;
c = this.read();
}
int res = 0;
while (c >= 48 && c <= 57) {
res *= 10;
res += c - 48;
c = this.read();
if (isSpaceChar(c)) {
return res * sgn;
}
}
throw new InputMismatchException();
}
public String next() {
int c;
while (isSpaceChar(c = this.read())) {
;
}
StringBuilder result = new StringBuilder();
result.appendCodePoint(c);
while (!isSpaceChar(c = this.read())) {
result.appendCodePoint(c);
}
return result.toString();
}
public static boolean isSpaceChar(int c) {
return c == 32 || c == 10 || c == 13 || c == 9 || c == -1;
}
}
static class OutputWriter {
private final PrintWriter writer;
public OutputWriter(OutputStream outputStream) {
writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(outputStream)));
}
public OutputWriter(Writer writer) {
this.writer = new PrintWriter(writer);
}
public void print(int[] array) {
for (int i = 0; i < array.length; i++) {
if (i != 0) {
writer.print(' ');
}
writer.print(array[i]);
}
}
public void println(int[] array) {
print(array);
writer.println();
}
public void close() {
writer.close();
}
public void println(int i) {
writer.println(i);
}
}
static class Basis {
public int size;
public long[] basis;
public Basis() {
basis = new long[100];
size = 0;
}
public boolean add(long x) {
for (int i = size - 1; i >= 0; i--) {
x = Math.min(x, x ^ basis[i]);
}
if (x == 0) return false;
basis[size++] = x;
for (int i = size - 2; i >= 0; i--) {
if (basis[i] > basis[i + 1]) {
long t = basis[i + 1];
basis[i + 1] = basis[i];
basis[i] = t;
}
}
return true;
}
}
}
Hello everybody!
On Mar 3, 10:00 Moscow time, Round 1 of Yandex.Algorithm 2018 competition will take place. I wrote the majority of the problems in this contest, with some additional help from GlebsHP.
I would like to thank GlebsHP for all his help with coordinating this round, MikeMirzayanov for polygon, and of course, everyone who took the time to test this round.
See you in the competition soon!
Editorial here: http://codeforces.net/blog/entry/58135
Hi! Topcoder SRM 730 will happen soon.
Time: 7:00am EDT Tuesday, February 20, 2018
Calendar: https://www.topcoder.com/community/events/
I'm the writer of this round. Hope to see you all participate!
Here's the editorial. Hope you have a happy new year!
Code can be found here: https://www.dropbox.com/sh/i9cxj44tvv5pqvn/AACQs7LLNyTZT-Gt_AMf7UQFa?dl=0
Let's start off a bit more abstractly. We would like to know if the statement "if P then Q" is true, where P and Q are some statements (in this case, P is "card has vowel", and Q is "card has even number"). To do determine this, we need to flip over any cards which could be counter-examples (i.e. could make the statement false).
Let's look at the truth table for if P then Q (see here: http://www.math.hawaii.edu/~ramsey/Logic/IfThen.html). The statement is only false when Q is false and P is true. Thus, it suffices to flip cards when P is true or Q is false.
To solve this problem, we need to print the count of vowels and odd digits in the string.
First solve: ksun48 at 00:01:01
Breakdown of results for submissions that passed pretests
OK 6427 (98.74%)
CHALLENGED 60 (0.92%)
WRONG_ANSWER 22 (0.34%)
TOTAL 6509
This problem is intended as an implementation problem. The bounds are small enough that a brute force works. We can iterate through all mapping of numbers to directions (i.e. using next permutation in C++ or doing some recursive DFS if there is no built in next permutation in your language), and simulate the robot's movements. We have to be careful that if the robot ever gets in an invalid state, we break out early and say the mapping is invalid.
First solve: jonathanirvings, dotorya at 00:05:16
Breakdown of results for submissions that passed pretests
OK 4192 (83.72%)
WRONG_ANSWER 652 (13.02%)
CHALLENGED 126 (2.52%)
RUNTIME_ERROR 33 (0.66%)
TIME_LIMIT_EXCEEDED 4 (0.08%)
TOTAL 5007
This is another simulation problem with some geometry. As we push a disk, we can iterate through all previous disks and see if their x-coordinates are ≤ 2r. If so, then that means these two circles can possibly touch.
If they do, we can compute the difference of heights between these two circles using pythagorean theorem. In particular, we want to know the change in y coordinate between the two touching circles. We know the hypotenuse (it is 2r since the circles are touching), and the change in x-coordinate is given, so the change in y coordinate is equal to 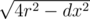 , where dx is the change in x-coordinate.
, where dx is the change in x-coordinate.
We can then take the maximum over all of these cases to get our final y-coordinate, since this is where this disk will first stop. Overall, this takes O(n2) time.
First solve: ehnryx at 00:04:05
Breakdown of results for submissions that passed pretests
OK 2694 (63.81%)
WRONG_ANSWER 1064 (25.20%)
CHALLENGED 448 (10.61%)
RUNTIME_ERROR 11 (0.26%)
TIME_LIMIT_EXCEEDED 4 (0.09%)
MEMORY_LIMIT_EXCEEDED 1 (0.02%)
TOTAL 4222
The main trickiness of this problem is that the sequence could potentially get arbitrary long, but we want an exact answer. In particular, it helps to think about how to reduce this problem to figuring out what state we need to maintain from a prefix of the sequence we've built in order to simulate our algorithm correctly. This suggests a dynamic programming approach.
For our dp state, we need to keep track of something in our prefix. First, the most obvious candidate is we need to keep track of the number of times 'ab' occurs in the prefix (this is so we know when to stop). However, using only this is not enough, as we can't distinguish between the sequences 'ab' and 'abaaaa'. So, this suggests we also need to keep track of the number of 'a's.
Let dp[i][j] be the expected answer given that there are i subsequences of the form 'a' in the prefix and j subsequences of the form 'ab' in the prefix.
Then, we have something like dp[i][j] = (pa * dp[i + 1][j] + pb * dp[i][i + j]) / (pa + pb). The first term in this sum comes from adding another 'a' to our sequence, and the second comes from adding a 'b' to our sequence. We also have dp[i][j] = j if j ≥ k as a base case. The answer should be dp[0][0].
However, if we run this as is, we'll notice there are still some issues. One is that i can get arbitrarily large here, as we can keep adding 'a's indefinitely. Instead, we can modify our base case to when i + j ≥ k. In this case, the next time we get a 'b', we will stop, so we can find a closed form for this scenario. The second is that any 'b's that we get before any occurrences of 'a' can essentially be ignored. To fix this, we can adjust our answer to be dp[1][0].
First solve: dotorya at 00:16:46
Breakdown of results for submissions that passed pretests
OK 449 (99.78%)
WRONG_ANSWER 1 (0.22%)
TOTAL 450
Let's ignore T for now, and try to characterize good sets S.
For every bit position i, consider the bitwise AND of all elements of S which have the i-th bit on (note, there is at least one element in S which has the i-th bit on, since we can always 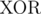 by m). We can see that this is equivalent to the smallest element of S that contains the i-th bit. Denote the resulting number as f(i).
by m). We can see that this is equivalent to the smallest element of S that contains the i-th bit. Denote the resulting number as f(i).
We can notice that this forms a partition of the bit positions, based on the final element that we get. In particular, there can't be a scenario where there is two positions x, y with 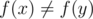 such that
such that 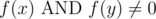 . To show this, let
. To show this, let 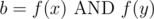 , and without loss of generality, let's assume
, and without loss of generality, let's assume 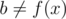 (it can't be simultaneously equal to f(x), f(y) since
(it can't be simultaneously equal to f(x), f(y) since 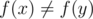 ). If the x-th bit in b is on, we get a contradiction, since b is a smaller element than f(x) that contains the x-th bit. If the x-th bit in b is off, then,
). If the x-th bit in b is on, we get a contradiction, since b is a smaller element than f(x) that contains the x-th bit. If the x-th bit in b is off, then, 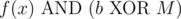 is a smaller element of S that contains the x-th bit.
is a smaller element of S that contains the x-th bit.
So, we can guess at this point that good sets S correspond to partitions of {1, 2, ..., m} one to one.
Given a partition, we can construct a valid good set as follows. We can observe that a good set S must be closed under bitwise OR also. To prove this, for any two elements 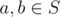 ,
, 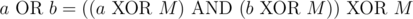 . Since the latter is some composition of XORs and ANDs, it it also in S. So, given a partition, we can take all unions of some subset of the partitions to get S.
. Since the latter is some composition of XORs and ANDs, it it also in S. So, given a partition, we can take all unions of some subset of the partitions to get S.
For an actual solution, partitions can be computed with bell numbers, which is an O(m2) dp (see this: http://mathworld.wolfram.com/BellNumber.html ).
Now, back to T, we can see that this decides some partitions beforehand. In particular, for each bit position, we can make a n-bit mask denoting what its value is in each of the n given values. The partitions are based on what these masks are. We can find what the sizes of these splits are, then multiply the ways to partition each individual split together to get the answer.
First solve: Petr at 00:26:54
Breakdown of results for submissions that passed pretests
OK 166 (100.00%)
TOTAL 166
Let's make a few simplifying observations
- It is not optimal to connect a red and blue point directly: Neither Roy or Biv will see this edge.
- If we have a sequence like red green red (or similarly blue green blue), it is not optimal to connect the outer two red nodes. We can replace the outer edge with two edges that have the same weight. This replacement will form some cycle in the red-green points, so we can remove one of these edges for a cheaper cost.
With these two observations, we can construct a solution as follows. First, split the points by the green points. Each section is now independent. There are then two cases, the outer green points are not directly connected, in which case, we must connect all the red/blue points in the line (for 2 * length of segment weight), or the outer green points are directly connected, in which case, we can omit the heaviest red and blue segment (for 3 * length of segment — heaviest red — heaviest blue). Thus, this problem can be solved in linear time.
Be careful about the case with no green points.
First solve: Petr at 00:38:32
Breakdown of results for submissions that passed pretests
OK 246 (90.44%)
WRONG_ANSWER 24 (8.82%)
RUNTIME_ERROR 2 (0.74%)
TOTAL 272
This is a digit dp problem. Let's try to solve the subproblem "How many ways can the i-th digit be at least j?". Let's fix j, and solve this with dp. We have a dp state dp[a][b][c] = number of ways given we've considered the first a digits of X, we need b more occurrences of digits at least j, and c is a boolean saying whether or not we are strictly less than X or not yet.
For a fixed digit, we can compute this dp table in O(n2) time, and then compute the answers to our subproblem for each i (i.e. by varying b in our table).
First solve: dotorya at 00:49:58
Breakdown of results for submissions that passed pretests
OK 46 (100.00%)
TOTAL 46
First, let's find connected components using only AND edges. If there are any XOR edges between two nodes in the same component, the answer is -1.
Now, we can place all components in a line. However, it may be optimal to merge some components together. It only makes sense to merge components of size 2 or more, of which there are at most k = n / 2 of them.
We can make a new graph with these k components. Two components have an edge if all of the edges between them are OR edges, otherwise, there is no edge.
We want to know what is the minimum number of cliques needed to cover all the nodes in this graph. To solve this, we can precompute which subsets of nodes forms a clique and put this into some array. Then, we can use the fast walsh hadamard transform to multiply this array onto itself until the element 2k - 1 is nonzero. Naively, this is O(2k * k2), but we can save a factor of k by noticing we only need to compute the last element, and we don't need to re-transform our input array at each iteration.
First solve: dotorya at 01:49:01
Breakdown of results for submissions that passed pretests
OK 10 (100.00%)
TOTAL 10
Hello everyone!
Another year has gone by. The last Codeforces contest of this year will be tomorrow, 29 Dec, 15:35 UTC.
The round details:
- combined div1+div2
- 8 problems
- 2.5 hours
- rated!!!
I'd like to thank the following people for helping with the round: KAN, winger, AlexFetisov, zemen, xiaowuc1, MikeMirzayanov. Without them, this round would not have been possible.
Scoring distribution will be posted later. Make sure to read ahead on the problems, since there may be some later problems that are easier for you. I hope to see you all at the contest, and good luck on the last chance to increase your rating this year!
EDIT1: The scoring distribution is 500-750-1000-1750-1750-2000-2750-3500
EDIT2: There will be a five minute delay for starting.
EDIT3: Editorial is here: http://codeforces.net/blog/entry/56713
EDIT4: Congratulations to the winners!
On Sunday, August 6th, 22:00 IST, we will hold the 2nd elimination for IndiaHacks (some more details here). The top 900 individuals who qualified through previous rounds will have the opportunity to participate in this round. The top 25 global participants and top 25 Indian participants will advance to the final round. The link to the contest is here.
After the official round is over, the next morning, on Monday, August 7th, 11:35 IST, we'll hold an unofficial unrated mirror here on Codeforces. This mirror will have ICPC rules. For participants of the official round, please hold off on discussing the problems publicly until after this mirror is over.
I was the author of the problems in this set, and I hope you will enjoy the problems. I would like to thank zemen for testing the set, Arpa for writing editorials, r3gz3n for his help on the HackerEarth side, KAN for helping us set up the mirror contest, and of course MikeMirzayanov for the great Polygon/Codeforces platform.
The round will consist of 6 problems and you will have 3 hours to complete them. Please note that the problems will be randomly arranged in both rounds, since I couldn't figure out how to sort them by difficulty. Be sure to read all the problems.
UPD1: Updated time of official round and posted link to contest.
UPD2: We should have updated the leaderboard to accept solutions that followed the first version of the first problem. We have also increased the number of finalists to 60 total (30 global + 30 indian) based on this new leaderboard.
UPD3: Here is the list of qualifiers. Congratulations to everyone.
Didn't notice a post from cgy4ever.
Topcoder SRM 718 will happen in ~4 hours.
Hello everyone!
I would like to invite you to participate in Hackerearth June Circuits 2017. It's a long contest that will start on June 16, 2017, 21:00 IST (check your timezone). The contest will run for 9 days.
The problemset consists of 7 traditional algorithmic tasks and 1 approximate problem. For traditional algorithmic tasks, you will receive points for every test case your solution passes — so you can get some points with partial solutions as well. For the approximation task, your score depends on the best solution in the contest so far. Check contest page for more details about in-contest schedule and rules.
I'm the tester of the problemset you'll have to work on — thanks to jtnydv25, saatwik27, harshil, zscoder, Arunnsit for preparing these tasks.
As usual, there will be some prizes for the top five competitors:
- $100 Amazon gift card + HE t-shirt.
- $75 Amazon gift card + HE t-shirt.
- $50 Amazon gift card + HE t-shirt.
- HE t-shirt.
- HE t-shirt.
Good luck to everyone, and I hope to see you at the contest :)
Some casework: First, let’s assume n != 0:
- If k = 0, then, a=0,b=0,
- If k = 1, then, a=n,b=2*n,
- If k = 2, then, a=0,b=n,
- If k = 3, then, a=n,b=0,
For k >= 4, we can show it is not possible.
There are two phases, one where two adjacent terms have opposite signs, and one where two adjacent terms have the same sign.
For the first phase, this kind of looks like the gcd algorithm, so we can show that the absolute value of sequence is strictly decreasing for even and odd indices separately until one of them hits zero, or two adjacent terms get the same sign.
For the second phase, we can show the absolute value increases.
A number can only appear at most once in the first phase, and at most twice in the second phase.
n=0 is a special case. We can show that it can only appear at most once, or an infinite number of times.
Make sure to watch out for the case 0 0 also.
n,k = map(int, raw_input().split())
if n != 0:
x = [n,0,n,2*n]
if k == 0:
print "Yes"
print 0,0
elif 1 <= k <= 3:
print "Yes"
print x[3-k], x[4-k]
else:
print "No"
else:
if k == 0:
print "Yes"
print 1,1
elif k == 1:
print "Yes"
print 0,1
else:
print "No"
Note that the operations are reversible, so it suffices to see if the two configurations can reach any common state.
Let’s denote the canonical state to be where we merge tokens as much as possible, and after this, move the tokens to the lowest indexed nodes that they can reach. Note we can do this, since merging tokens allows us to travel across more edges. We show how we can simulate this process in O((n+m) * c) time.
For instance, we can simulate this process c times. For each token, find the set of nodes it can reach. If two tokens or more tokens can reach the same node, merge them. We only need to do this process c times since there can only be at most c merges. This process takes O(n+m) overall for all tokens (i.e. we only visit each node/edge at most once per iteration).
Thus, checking if a sequence of moves is possible is to check whether the canonical states of both the initial and final states are identical.
import java.io.OutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.io.BufferedWriter;
import java.util.InputMismatchException;
import java.io.IOException;
import java.util.ArrayList;
import java.util.List;
import java.io.Writer;
import java.io.OutputStreamWriter;
import java.util.Collections;
import java.io.InputStream;
/**
* Built using CHelper plug-in
* Actual solution is at the top
*/
public class Main {
public static void main(String[] args) {
InputStream inputStream = System.in;
OutputStream outputStream = System.out;
InputReader in = new InputReader(inputStream);
OutputWriter out = new OutputWriter(outputStream);
RainbowRoad solver = new RainbowRoad();
int testCount = Integer.parseInt(in.next());
for (int i = 1; i <= testCount; i++)
solver.solve(i, in, out);
out.close();
}
static class RainbowRoad {
public List<RainbowRoad.Edge>[] edges;
public int[] par;
public int[] size;
public int[] mn;
public long[] ccolor;
public int n;
public int m;
public int c;
public boolean[] vis;
public void solve(int testNumber, InputReader in, OutputWriter out) {
n = in.nextInt();
m = in.nextInt();
c = in.nextInt();
edges = new List[n];
for (int i = 0; i < n; i++) edges[i] = new ArrayList<>();
for (int i = 0; i < m; i++) {
int a = in.nextInt() - 1, b = in.nextInt() - 1;
long c = in.nextLong();
edges[a].add(new RainbowRoad.Edge(a, b, c));
edges[b].add(new RainbowRoad.Edge(b, a, c));
}
int[] x = in.readIntArray(c);
int[] y = in.readIntArray(c);
for (int i = 0; i < c; i++) {
x[i]--;
y[i]--;
}
List<RainbowRoad.T> p = solve(x), q = solve(y);
out.println(p.equals(q) ? "Possible" : "Impossible");
}
public List<RainbowRoad.T> solve(int[] arr) {
par = new int[n];
size = new int[n];
mn = new int[n];
ccolor = new long[n];
for (int i = 0; i < n; i++) {
par[i] = i;
mn[i] = i;
size[i] = 1;
ccolor[i] = 0;
}
for (int j = 0; j < c; j++) {
ccolor[arr[j]] |= 1L << j;
}
for (int xx = 0; xx < c; xx++) {
vis = new boolean[n];
for (int i = 0; i < n; i++) {
if (!vis[i] && ccolor[find(i)] != 0)
dfs(i);
}
}
List<RainbowRoad.T> ret = new ArrayList<>();
for (int i = 0; i < n; i++) {
if (find(i) == i && ccolor[i] != 0) {
ret.add(new RainbowRoad.T(mn[i], ccolor[i]));
}
}
Collections.sort(ret);
return ret;
}
public void dfs(int node) {
if (vis[node]) return;
vis[node] = true;
for (RainbowRoad.Edge next : edges[node]) {
if (join(next.a, next.b, next.c)) {
dfs(next.b);
}
}
}
public int find(int x) {
return x == par[x] ? x : (par[x] = find(par[x]));
}
public boolean join(int a, int b, long c) {
int x = find(a), y = find(b);
if (x == y) return false;
if ((ccolor[x] & c) != c && (ccolor[y] & c) != c) return false;
if (size[x] < size[y]) {
int t = x;
x = y;
y = t;
}
size[x] += size[y];
mn[x] = Math.min(mn[x], mn[y]);
par[y] = x;
ccolor[x] |= ccolor[y];
return true;
}
static class Edge {
public int a;
public int b;
public long c;
public Edge(int a, int b, long c) {
this.a = a;
this.b = b;
this.c = c;
}
}
static class T implements Comparable<RainbowRoad.T> {
public long color;
public int pos;
public T(int pos, long color) {
this.pos = pos;
this.color = color;
}
public boolean equals(Object o) {
if (!(o instanceof RainbowRoad.T)) return false;
return ((RainbowRoad.T) o).pos == pos && ((RainbowRoad.T) o).color == color;
}
public int compareTo(RainbowRoad.T other) {
return pos - other.pos;
}
public String toString() {
return pos + " " + color;
}
}
}
static class InputReader {
private InputStream stream;
private byte[] buf = new byte[1024];
private int curChar;
private int numChars;
public InputReader(InputStream stream) {
this.stream = stream;
}
public int[] readIntArray(int tokens) {
int[] ret = new int[tokens];
for (int i = 0; i < tokens; i++) {
ret[i] = nextInt();
}
return ret;
}
public int read() {
if (this.numChars == -1) {
throw new InputMismatchException();
} else {
if (this.curChar >= this.numChars) {
this.curChar = 0;
try {
this.numChars = this.stream.read(this.buf);
} catch (IOException var2) {
throw new InputMismatchException();
}
if (this.numChars <= 0) {
return -1;
}
}
return this.buf[this.curChar++];
}
}
public int nextInt() {
int c;
for (c = this.read(); isSpaceChar(c); c = this.read()) {
;
}
byte sgn = 1;
if (c == 45) {
sgn = -1;
c = this.read();
}
int res = 0;
while (c >= 48 && c <= 57) {
res *= 10;
res += c - 48;
c = this.read();
if (isSpaceChar(c)) {
return res * sgn;
}
}
throw new InputMismatchException();
}
public long nextLong() {
int c;
for (c = this.read(); isSpaceChar(c); c = this.read()) {
;
}
byte sgn = 1;
if (c == 45) {
sgn = -1;
c = this.read();
}
long res = 0L;
while (c >= 48 && c <= 57) {
res *= 10L;
res += (long) (c - 48);
c = this.read();
if (isSpaceChar(c)) {
return res * (long) sgn;
}
}
throw new InputMismatchException();
}
public String next() {
int c;
while (isSpaceChar(c = this.read())) {
;
}
StringBuilder result = new StringBuilder();
result.appendCodePoint(c);
while (!isSpaceChar(c = this.read())) {
result.appendCodePoint(c);
}
return result.toString();
}
public static boolean isSpaceChar(int c) {
return c == 32 || c == 10 || c == 13 || c == 9 || c == -1;
}
}
static class OutputWriter {
private final PrintWriter writer;
public OutputWriter(OutputStream outputStream) {
writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(outputStream)));
}
public OutputWriter(Writer writer) {
this.writer = new PrintWriter(writer);
}
public void print(Object... objects) {
for (int i = 0; i < objects.length; i++) {
if (i != 0) {
writer.print(' ');
}
writer.print(objects[i]);
}
}
public void println(Object... objects) {
print(objects);
writer.println();
}
public void close() {
writer.close();
}
}
}
First, handle some special cases where the sequence doesn't start or end with '*', or contains no '*' (also, be careful when the pattern’s length is bigger than r-l+1). So, now, let's assume the sequence starts and ends with '*'.
We can proceed greedily. First, split the pattern by '*'. For each contiguous substring of letters, we can greedily take the earliest occurrence after a certain position. For each length <= 10 substring of the input, we can build a sorted vector of positions that it occurs in. The next earliest occurrence can be found using lower_bound.
import java.io.OutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.io.BufferedWriter;
import java.util.HashMap;
import java.util.InputMismatchException;
import java.io.IOException;
import java.util.ArrayList;
import java.io.Writer;
import java.io.OutputStreamWriter;
import java.util.Collections;
import java.io.InputStream;
/**
* Built using CHelper plug-in
* Actual solution is at the top
*/
public class Main {
public static void main(String[] args) {
InputStream inputStream = System.in;
OutputStream outputStream = System.out;
InputReader in = new InputReader(inputStream);
OutputWriter out = new OutputWriter(outputStream);
WildcardWords solver = new WildcardWords();
solver.solve(1, in, out);
out.close();
}
static class WildcardWords {
public HashMap<String, ArrayList<Integer>> mp;
public void solve(int testNumber, InputReader in, OutputWriter out) {
char[] s = in.next().toCharArray();
mp = new HashMap<>();
for (int i = 0; i < s.length; i++) {
String cur = "";
for (int j = i; j < i + 10 && j < s.length; j++) {
cur += s[j];
ArrayList<Integer> x = mp.get(cur);
if (x == null) {
mp.put(cur, x = new ArrayList<>());
}
x.add(i);
}
}
int q = in.nextInt();
while (q-- > 0) {
int l = in.nextInt() - 1, r = in.nextInt();
String w = in.next();
if (!w.contains("*")) {
if (r - l != w.length()) {
out.println("No");
continue;
}
String ee = "";
for (int i = l; i < r; i++) ee += s[i];
out.println(ee.equals(w) ? "Yes" : "No");
continue;
}
String[] pat = w.split("\\*");
int cur = l;
if (w.charAt(0) != '*') {
// must start with pat[0]
int d = getPos(pat[0], cur);
if (d != cur) {
cur = 1 << 29;
} else {
cur = d + pat[0].length();
}
}
for (int i = 1; i < pat.length; i++) {
if (pat[i].equals("")) continue;
cur = next(pat[i], cur);
}
int c = pat.length - 1;
out.println((w.charAt(w.length() - 1) == '*' ? cur <= r :
(cur <= r && getPos(pat[c], r - pat[c].length()) == r - pat[c].length())) ? "Yes" : "No");
}
}
public int next(String s, int start) {
if (start == 1 << 29) return 1 << 29;
int k = getPos(s, start);
if (k == 1 << 29) return k;
return k + s.length();
}
public int getPos(String s, int start) {
ArrayList<Integer> w = mp.get(s);
if (w == null) {
return 1 << 29;
}
int pos = Collections.binarySearch(w, start);
if (pos < 0) pos = -pos - 1;
if (pos == w.size()) {
return 1 << 29;
}
return w.get(pos);
}
}
static class OutputWriter {
private final PrintWriter writer;
public OutputWriter(OutputStream outputStream) {
writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(outputStream)));
}
public OutputWriter(Writer writer) {
this.writer = new PrintWriter(writer);
}
public void print(Object... objects) {
for (int i = 0; i < objects.length; i++) {
if (i != 0) {
writer.print(' ');
}
writer.print(objects[i]);
}
}
public void println(Object... objects) {
print(objects);
writer.println();
}
public void close() {
writer.close();
}
}
static class InputReader {
private InputStream stream;
private byte[] buf = new byte[1024];
private int curChar;
private int numChars;
public InputReader(InputStream stream) {
this.stream = stream;
}
public int read() {
if (this.numChars == -1) {
throw new InputMismatchException();
} else {
if (this.curChar >= this.numChars) {
this.curChar = 0;
try {
this.numChars = this.stream.read(this.buf);
} catch (IOException var2) {
throw new InputMismatchException();
}
if (this.numChars <= 0) {
return -1;
}
}
return this.buf[this.curChar++];
}
}
public int nextInt() {
int c;
for (c = this.read(); isSpaceChar(c); c = this.read()) {
;
}
byte sgn = 1;
if (c == 45) {
sgn = -1;
c = this.read();
}
int res = 0;
while (c >= 48 && c <= 57) {
res *= 10;
res += c - 48;
c = this.read();
if (isSpaceChar(c)) {
return res * sgn;
}
}
throw new InputMismatchException();
}
public String next() {
int c;
while (isSpaceChar(c = this.read())) {
;
}
StringBuilder result = new StringBuilder();
result.appendCodePoint(c);
while (!isSpaceChar(c = this.read())) {
result.appendCodePoint(c);
}
return result.toString();
}
public static boolean isSpaceChar(int c) {
return c == 32 || c == 10 || c == 13 || c == 9 || c == -1;
}
}
}
Just simulate the process.
Extension: solve this when n <= 10^5, |x_i|,|y_i| <= 10^5.
n = int(raw_input())
D = dict()
def go(x, y):
if not (x, y) in D:
D[(x, y)] = 0
D[(x, y)] = D[(x, y)] + 1
if D[(x, y)] == 5:
del D[(x, y)]
go(x + 1, y)
go(x, y + 1)
go(x - 1, y)
go(x, y - 1)
for i in range(n):
x, y = map(int, raw_input().split())
go(x, y)
print len(D)
First, we need to reduce it to a counting problem.
Let the sequence be a1, a2, ..., as Let's fix a prefix of the given sequence: x1, x2, ..., xp, where xi = ai for 1 ≤ i ≤ p. Now, fix xp + 1 < ap + 1, and xp + 1! = xp.
We can compute the frequency of the remaining colors. So, we want to solve this problem: How many ways are there to arrange balls of c colors with bi balls of the i-th color, such that the first ball in the line cannot be color 1.
We can solve this using dynamic programming by adding colors one by one, or inclusion exclusion.
For the inclusion exclusion solution, let's first ignore color 1.
We want to count the number of sequences where no two adjacent balls are the same color. Let's partition the sequence into "groups", where a group is a sequence of adjacent balls of the same color (not necessarily maximal).
Then, the final answer can be computed as cS - cS - 1 + cS - 2 - ....
Let's look at one color, let's say it's color j. We can precompute the number of ways to partition this into y groups. This is the number of ways to partition bj into y summands. This can be computed with a dp.
Now, let's consider compute ck. We need to assign yi groups into color i such that 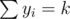 . Thus, this can be computed with a knapsack like formula. After assigning these, we can rearrange groups freely, for a total of k! ways.
. Thus, this can be computed with a knapsack like formula. After assigning these, we can rearrange groups freely, for a total of k! ways.
Now, let's add color 1 back in. Let's fix the number of other color groups k, and also the number of groups for color 1 (call it k1). Then, instead of multiplying by (k + k0)!, we can multiply by 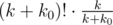 .
.
Overall, we need to solve (sum a) * (max a) counting problems, each of which takes len(a) * max(a) * sum(a) time. The overall running time is thus 15^7 (in practice, the constant is much lower, since not all counting problems will be the maximal ones).
import java.io.OutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.io.BufferedWriter;
import java.io.Writer;
import java.io.OutputStreamWriter;
import java.util.InputMismatchException;
import java.io.IOException;
import java.io.InputStream;
/**
* Built using CHelper plug-in
* Actual solution is at the top
*/
public class Main {
public static void main(String[] args) {
InputStream inputStream = System.in;
OutputStream outputStream = System.out;
InputReader in = new InputReader(inputStream);
OutputWriter out = new OutputWriter(outputStream);
AvoidingAdjacent solver = new AvoidingAdjacent();
solver.solve(1, in, out);
out.close();
}
static class AvoidingAdjacent {
public int mod = 1000000007;
public int MAXN = 16 * 16 + 1;
public int[][] w1;
public long[] fact;
public long[] ifact;
public void solve(int testNumber, InputReader in, OutputWriter out) {
int c = in.nextInt();
int[] arr = in.readIntArray(c);
int s = AUtils.sum(arr);
int[] x = in.readIntArray(s);
for (int i = 0; i < s; i++) x[i]--;
long[][] e = Factorials.getFIF(MAXN, mod);
fact = e[0];
ifact = e[1];
w1 = new int[MAXN][MAXN];
w1[0][0] = 1;
for (int i = 1; i < MAXN; i++) {
for (int j = 1; j < MAXN; j++) {
for (int k = 1; k <= i; k++) {
w1[i][j] += w1[i - k][j - 1];
if (w1[i][j] >= mod) w1[i][j] -= mod;
}
}
}
int ans = 0;
for (int i = 0; i < s; i++) {
for (int j = 0; j < x[i]; j++) {
if (i > 0 && j == x[i - 1]) continue;
if (arr[j] > 0) {
arr[j]--;
int w = solve(arr, j);
ans += w;
if (ans >= mod) ans -= mod;
arr[j]++;
}
}
arr[x[i]]--;
}
out.println((ans + 1) % mod);
}
public int solve(int[] freq, int special) {
int d = AUtils.sum(freq);
int b = AUtils.max(freq);
if (d == 0) return 1;
if (d == freq[special]) return 0;
if (b + b - 1 > d) return 0;
int[] dp = new int[1];
dp[0] = 1;
for (int j = 0; j < freq.length; j++) {
if (freq[j] == 0 || j == special) continue;
int[] nxt = new int[dp.length + freq[j]];
for (int pgr = 0; pgr < dp.length; pgr++) {
for (int cgr = 1; cgr <= freq[j]; cgr++) {
nxt[pgr + cgr] += 1L * dp[pgr] * w1[freq[j]][cgr] % mod * ifact[cgr] % mod;
if (nxt[pgr + cgr] >= mod) nxt[pgr + cgr] -= mod;
}
}
dp = nxt;
}
int res = 0;
for (int i = 0; i < dp.length; i++) {
if (freq[special] == 0) {
long x = 1L * dp[i] * fact[i] % mod;
if ((d - i) % 2 == 0) res += x;
else res -= x;
if (res >= mod) res -= mod;
if (res < 0) res += mod;
} else {
for (int j = 1; j <= freq[special]; j++) {
long x = 1L * dp[i] * w1[freq[special]][j] % mod * ifact[j] % mod;
x = x * fact[i + j - 1] % mod * i % mod;
if ((d - i - j) % 2 == 0) res += x;
else res -= x;
if (res >= mod) res -= mod;
if (res < 0) res += mod;
}
}
}
return res;
}
}
static class AUtils {
public static int max(int[] arr) {
int res = arr[0];
for (int x : arr) res = Math.max(res, x);
return res;
}
public static int sum(int[] arr) {
int sum = 0;
for (int x : arr) {
sum += x;
}
return sum;
}
}
static class OutputWriter {
private final PrintWriter writer;
public OutputWriter(OutputStream outputStream) {
writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(outputStream)));
}
public OutputWriter(Writer writer) {
this.writer = new PrintWriter(writer);
}
public void close() {
writer.close();
}
public void println(int i) {
writer.println(i);
}
}
static class InputReader {
private InputStream stream;
private byte[] buf = new byte[1024];
private int curChar;
private int numChars;
public InputReader(InputStream stream) {
this.stream = stream;
}
public int[] readIntArray(int tokens) {
int[] ret = new int[tokens];
for (int i = 0; i < tokens; i++) {
ret[i] = nextInt();
}
return ret;
}
public int read() {
if (this.numChars == -1) {
throw new InputMismatchException();
} else {
if (this.curChar >= this.numChars) {
this.curChar = 0;
try {
this.numChars = this.stream.read(this.buf);
} catch (IOException var2) {
throw new InputMismatchException();
}
if (this.numChars <= 0) {
return -1;
}
}
return this.buf[this.curChar++];
}
}
public int nextInt() {
int c;
for (c = this.read(); isSpaceChar(c); c = this.read()) {
;
}
byte sgn = 1;
if (c == 45) {
sgn = -1;
c = this.read();
}
int res = 0;
while (c >= 48 && c <= 57) {
res *= 10;
res += c - 48;
c = this.read();
if (isSpaceChar(c)) {
return res * sgn;
}
}
throw new InputMismatchException();
}
public static boolean isSpaceChar(int c) {
return c == 32 || c == 10 || c == 13 || c == 9 || c == -1;
}
}
static class Factorials {
public static long[][] getFIF(int max, int mod) {
long[] fact = new long[max];
long[] ifact = new long[max];
long[] inv = new long[max];
inv[1] = 1;
for (int i = 2; i < max; i++) {
inv[i] = (mod - mod / i) * inv[mod % i] % mod;
}
fact[0] = 1;
ifact[0] = 1;
for (int i = 1; i < max; i++) {
fact[i] = fact[i - 1] * i % mod;
ifact[i] = ifact[i - 1] * inv[i] % mod;
}
return new long[][]{fact, ifact, inv};
}
}
}
We can look at this backwards. Consider a position for which Bob can make no more moves. Then, we have a token in every node in the tree except for the special vertex. To maximize the number of tokens that Alice can place, we can push these tokens as far away as we can from the special vertex (i.e. remove this token, and place 2 tokens on one of its children).
So, after fixing a special node, and rooting the tree at the special node, the answer is the sum over nodes of 2^d, where d is longest path from node to a leaf without going up the tree.This can be computed in O(n) time for a single node.
Now, let’s look at what happens when we move the special node to an adjacent vertex. We just need to add contribution of old vertex and subtract contribution of new vertex. These can be done if we keep track of the longest and second longest path at each node.
import java.io.OutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.util.List;
import java.io.BufferedWriter;
import java.io.Writer;
import java.io.OutputStreamWriter;
import java.util.InputMismatchException;
import java.io.IOException;
import java.util.ArrayList;
import java.io.InputStream;
/**
* Built using CHelper plug-in
* Actual solution is at the top
*/
public class Main {
public static void main(String[] args) {
InputStream inputStream = System.in;
OutputStream outputStream = System.out;
InputReader in = new InputReader(inputStream);
OutputWriter out = new OutputWriter(outputStream);
TokenTree solver = new TokenTree();
solver.solve(1, in, out);
out.close();
}
static class TokenTree {
int mod = 1000000007;
int[] pow2;
List<Integer>[] graph;
int[] ans;
int[] down;
int[] up;
int[] b1;
int[] b2;
int[] id;
public void solve(int testNumber, InputReader in, OutputWriter out) {
int n = in.nextInt();
pow2 = new int[n + 1];
pow2[0] = 1;
for (int i = 1; i <= n; i++) {
pow2[i] = (pow2[i - 1] << 1) % mod;
}
graph = new List[n];
for (int i = 0; i < n; i++) graph[i] = new ArrayList<>();
for (int i = 0; i < n - 1; i++) {
int a = in.nextInt() - 1, b = in.nextInt() - 1;
graph[a].add(b);
graph[b].add(a);
}
ans = new int[n];
b1 = new int[n];
b2 = new int[n];
id = new int[n];
getFarthest();
for (int i = 1; i < n; i++) {
ans[0] += pow2[down[i]];
if (ans[0] >= mod) ans[0] -= mod;
}
dfs3(0, -1);
for (int i = 0; i < n; i++) {
out.println(ans[i]);
}
}
void dfs3(int node, int par) {
for (int next : graph[node]) {
if (next == par) continue;
ans[next] = ans[node] - pow2[down[next]];
if (ans[next] < 0) ans[next] += mod;
int add = b1[node];
if (id[node] == next) add = b2[node];
ans[next] += pow2[add];
if (ans[next] >= mod) ans[next] -= mod;
dfs3(next, node);
}
}
int[] getFarthest() {
int n = graph.length;
down = new int[n];
up = new int[n];
dfs(0, -1);
dfs2(0, -1, 0);
int[] ret = new int[n];
for (int i = 0; i < n; i++) {
ret[i] = Math.max(up[i], down[i]);
}
return ret;
}
void dfs(int node, int par) {
for (int next : graph[node]) {
if (next == par) continue;
dfs(next, node);
down[node] = Math.max(down[node], down[next] + 1);
}
}
void dfs2(int node, int par, int frompar) {
up[node] = frompar;
b1[node] = up[node];
id[node] = par;
int mx1 = 0, id1 = -1, mx2 = 0;
for (int next : graph[node]) {
if (next == par) continue;
if (down[next] + 1 > b1[node]) {
b2[node] = b1[node];
b1[node] = down[next] + 1;
id[node] = next;
} else if (down[next] + 1 > b2[node]) {
b2[node] = down[next] + 1;
}
if (down[next] + 1 > mx1) {
mx2 = mx1;
mx1 = down[next] + 1;
id1 = next;
} else if (down[next] + 1 > mx2) {
mx2 = down[next] + 1;
}
}
for (int next : graph[node]) {
if (next == par) continue;
dfs2(next, node, Math.max(up[node], next == id1 ? mx2 : mx1) + 1);
}
}
}
static class OutputWriter {
private final PrintWriter writer;
public OutputWriter(OutputStream outputStream) {
writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(outputStream)));
}
public OutputWriter(Writer writer) {
this.writer = new PrintWriter(writer);
}
public void close() {
writer.close();
}
public void println(int i) {
writer.println(i);
}
}
static class InputReader {
private InputStream stream;
private byte[] buf = new byte[1024];
private int curChar;
private int numChars;
public InputReader(InputStream stream) {
this.stream = stream;
}
public int read() {
if (this.numChars == -1) {
throw new InputMismatchException();
} else {
if (this.curChar >= this.numChars) {
this.curChar = 0;
try {
this.numChars = this.stream.read(this.buf);
} catch (IOException var2) {
throw new InputMismatchException();
}
if (this.numChars <= 0) {
return -1;
}
}
return this.buf[this.curChar++];
}
}
public int nextInt() {
int c;
for (c = this.read(); isSpaceChar(c); c = this.read()) {
;
}
byte sgn = 1;
if (c == 45) {
sgn = -1;
c = this.read();
}
int res = 0;
while (c >= 48 && c <= 57) {
res *= 10;
res += c - 48;
c = this.read();
if (isSpaceChar(c)) {
return res * sgn;
}
}
throw new InputMismatchException();
}
public static boolean isSpaceChar(int c) {
return c == 32 || c == 10 || c == 13 || c == 9 || c == -1;
}
}
}
Hello everybody!
On May 27, 23:00 Moscow time, Round 2 of Yandex.Algorithm competition will take place. I wrote the majority of the problems in this contest, with some additional help from Zlobober.
I would like to thank Zlobober for all his help with coordinating this round, MikeMirzayanov for polygon, and of course, everyone who took the time to test this round.
Please note, the problems will be randomly arranged, so make sure you read everything during the round :)
If you are using Java, please submit using Java 7 x32.
See you in the competition soon!
UPD 1: Editorial here: http://codeforces.net/blog/entry/52223
Hello everyone!
I would like to invite you to participate in Hackerearth April Circuits 2017. It's a long contest that will start on April 21, 21:00 IST (check your timezone). Contest will run for 9 days.
The problemset consists of 7 traditional algorithmic tasks and 1 approximate problem. For traditional algorithmic tasks, you will receive points for every test case your solution passes — so you can get some points with partial solutions as well. For the approximation task, your score depends on the best solution in the contest so far. Check contest page for more details about in-contest schedule and rules.
I'm the tester of the problemset you'll have to work on — thanks to jtnydv25, saatwik27, pkacprzak, r3gz3n, trytolearn for preparing these tasks.
As usual, there will be some nice prizes for the top five competitors:
- $100 Amazon gift card + HE t-shirt.
- $75 Amazon gift card + HE t-shirt.
- $50 Amazon gift card + HE t-shirt.
- HE t-shirt.
- HE t-shirt.
Good luck to everyone, and I hope to see you at the contest :)
print (lambda s: max((s[:i] + x + s[i+1:]).count("VK") for x in "VK" for i in range(len(s))))(raw_input())
print (lambda s: s.count("VK") + int(any(x*3 in "K" + s + "V" for x in "VK")))(raw_input())
x,y = raw_input(), raw_input()
print all(a>=b for a,b in zip(x,y)) * y or "-1"
#include <stdio.h>
#include <algorithm>
#include <assert.h>
using namespace std;
typedef long long ll;
typedef long double ld;
// Adjust MAXN for bounds
const ll MAXN=1e5+4;
// MAXV is the max amount of time we can take
const ld MAXV=1e18;
ll a[MAXN],b[MAXN];
ld exhaust[MAXN];
int n;
ll P;
bool f(ld imid) {
ld needsum=0;
for (int i=0;i<n;i++) {
ld need=max(0.0L, (imid-exhaust[i])*a[i]);
needsum+=need;
}
ld supply=imid*P;
return supply>=needsum;
}
int main()
{
scanf("%d%lld",&n,&P);
for (int i=0;i<n;i++) {
scanf("%lld%lld",&a[i],&b[i]);
}
ll suma=0;
for (int i=0;i<n;i++) {
suma+=a[i];
}
if (P>=suma) {
printf("-1\n");
return 0;
}
for (int i=0;i<n;i++) {
exhaust[i]=((ld)b[i])/((ld)a[i]);
}
ld imin=0,imax=MAXV;
for (ll iter=0;iter<220;iter++) {
ld imid=(imin+imax)/2;
if (f(imid)) imin=imid;
else imax=imid;
}
if (imax>MAXV-100) printf("-1\n");
else printf("%.9f\n",(double)imin);
}
#include <bits/stdc++.h>
using namespace std;
#define sim template < class c
#define ris return * this
#define dor > debug & operator <<
#define eni(x) sim > typename \
enable_if<sizeof dud<c>(0) x 1, debug&>::type operator<<(c i) {
sim > struct rge {c b, e; };
sim > rge<c> range(c i, c j) { return rge<c>{i, j}; }
sim > auto dud(c* x) -> decltype(cerr << *x, 0);
sim > char dud(...);
struct debug {
#ifdef LOCAL
~debug() { cerr << endl; }
eni(!=) cerr << boolalpha << i; ris; }
eni(==) ris << range(begin(i), end(i)); }
sim, class b dor(pair < b, c > d) {
ris << "(" << d.first << ", " << d.second << ")";
}
sim dor(rge<c> d) {
*this << "[";
for (auto it = d.b; it != d.e; ++it)
*this << ", " + 2 * (it == d.b) << *it;
ris << "]";
}
#else
sim dor(const c&) { ris; }
#endif
};
#define imie(...) " [" << #__VA_ARGS__ ": " << (__VA_ARGS__) << "] "
typedef long double ld;
typedef long double ll;
ld K(ld a) { return a * a; }
struct P {
ll x, y;
void read() { cin >> x >> y; }
P operator + (P b) { return P{x + b.x, y + b.y}; }
P operator - (P b) { return P{x - b.x, y - b.y}; }
P operator * (ld/*ll*/ mul) { return P{x * mul, y * mul}; }
ll operator * (P b) { return x * b.y - y * b.x; }
ll dot(P b) { return x * b.x + y * b.y; }
ld len() { return sqrt(K(x) + K(y)); }
P lenTo(ld to) { return *this * (to / len()); }
ld dist(P & b) { return (*this - b).len(); }
};
struct L2 {
P one, two;
ld dist(P he) {
return abs((he - one) * (he - two)) / one.dist(two);
}
};
int main() {
int n;
cin >> n;
vector<P> points(n);
for(P & p : points)
p.read();
ld answer = 1e15;
for(int i = 0; i < n; ++i)
for(int j = 0; j < 2 * n; ++j)
if(abs(i - j) <= 2)
for(int k = 0; k < 2 * n; ++k)
if(abs(i - k) <= 2 && (int) set<int>{i % n, j % n, k % n}.size() == 3)
answer = min(answer, L2{points[i%n], points[j%n]}.dist(points[k%n]));
printf("%.10lf\n", (double) answer / 2);
}
import java.io.OutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.io.BufferedWriter;
import java.io.Writer;
import java.io.OutputStreamWriter;
import java.util.InputMismatchException;
import java.io.IOException;
import java.io.InputStream;
/**
* Built using CHelper plug-in
* Actual solution is at the top
*/
public class Main {
public static void main(String[] args) {
InputStream inputStream = System.in;
OutputStream outputStream = System.out;
InputReader in = new InputReader(inputStream);
OutputWriter out = new OutputWriter(outputStream);
NonConvexPolygon solver = new NonConvexPolygon();
solver.solve(1, in, out);
out.close();
}
static class NonConvexPolygon {
public void solve(int testNumber, InputReader in, OutputWriter out) {
int n = in.nextInt();
long[][] p = new long[n][2];
for (int i = 0; i < n; i++) {
p[i][0] = in.nextInt();
p[i][1] = in.nextInt();
}
double ans = 1L << 60;
for (int i = 0; i < n; i++) {
int prev = (i + n - 1) % n, next = (i + 1) % n;
ans = Math.min(ans, PointToSegmentDistance.pointToLineThroughTwoPointsDistance(
p[i][0], p[i][1], p[prev][0], p[prev][1], p[next][0], p[next][1]
) / 2.0);
}
out.printf("%.10f\n", ans);
}
}
static class Utils {
public static double cross(Point a, Point b, Point c) {
Point ab = new Point(b.x - a.x, b.y - a.y);
Point ac = new Point(c.x - a.x, c.y - a.y);
return ab.x * ac.y - ab.y * ac.x;
}
}
static class PointToSegmentDistance {
static double fastHypot(double x, double y) {
return Math.sqrt(x * x + y * y);
}
public static double pointToLineThroughTwoPointsDistance(long x, long y, long ax, long ay, long bx, long by) {
double t = Utils.cross(new Point(ax, ay), new Point(bx, by), new Point(x, y));
return Math.abs(t / fastHypot(ax - bx, ay - by));
}
}
static class Point implements Comparable<Point> {
public double x;
public double y;
public double angle;
public int idx;
public Point(double x, double y) {
this.x = x;
this.y = y;
angle = 0;
}
public Point(double x, double y, int idx) {
this.x = x;
this.y = y;
this.idx = idx;
}
public int compareTo(Point other) {
return x == other.x ? (int) Math.signum(y - other.y) : (int) Math.signum(x - other.x);
}
}
static class OutputWriter {
private final PrintWriter writer;
public OutputWriter(OutputStream outputStream) {
writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(outputStream)));
}
public OutputWriter(Writer writer) {
this.writer = new PrintWriter(writer);
}
public void printf(String format, Object... objects) {
writer.printf(format, objects);
}
public void close() {
writer.close();
}
}
static class InputReader {
private InputStream stream;
private byte[] buf = new byte[1024];
private int curChar;
private int numChars;
public InputReader(InputStream stream) {
this.stream = stream;
}
public int read() {
if (this.numChars == -1) {
throw new InputMismatchException();
} else {
if (this.curChar >= this.numChars) {
this.curChar = 0;
try {
this.numChars = this.stream.read(this.buf);
} catch (IOException var2) {
throw new InputMismatchException();
}
if (this.numChars <= 0) {
return -1;
}
}
return this.buf[this.curChar++];
}
}
public int nextInt() {
int c;
for (c = this.read(); isSpaceChar(c); c = this.read()) {
;
}
byte sgn = 1;
if (c == 45) {
sgn = -1;
c = this.read();
}
int res = 0;
while (c >= 48 && c <= 57) {
res *= 10;
res += c - 48;
c = this.read();
if (isSpaceChar(c)) {
return res * sgn;
}
}
throw new InputMismatchException();
}
public static boolean isSpaceChar(int c) {
return c == 32 || c == 10 || c == 13 || c == 9 || c == -1;
}
}
}
#include <bits/stdc++.h>
using namespace std;
#define sim template < class c
#define ris return * this
#define dor > debug & operator <<
#define eni(x) sim > typename \
enable_if<sizeof dud<c>(0) x 1, debug&>::type operator<<(c i) {
sim > struct rge {c b, e; };
sim > rge<c> range(c i, c j) { return rge<c>{i, j}; }
sim > auto dud(c* x) -> decltype(cerr << *x, 0);
sim > char dud(...);
struct debug {
#ifdef LOCAL
~debug() { cerr << endl; }
eni(!=) cerr << boolalpha << i; ris; }
eni(==) ris << range(begin(i), end(i)); }
sim, class b dor(pair < b, c > d) {
ris << "(" << d.first << ", " << d.second << ")";
}
sim dor(rge<c> d) {
*this << "[";
for (auto it = d.b; it != d.e; ++it)
*this << ", " + 2 * (it == d.b) << *it;
ris << "]";
}
#else
sim dor(const c&) { ris; }
#endif
};
#define imie(...) " [" << #__VA_ARGS__ ": " << (__VA_ARGS__) << "] "
const int nax = 2e5 + 5;
bool forbidden[nax];
int my_gcd(int a, int b) {
if(a == 0 || b == 0) return max(a, b); // return m
return __gcd(a, b);
}
#define __gcd use____my_gcd
vector<int> which[nax];
pair<int,int> dp[nax];
int my_pow(int a, int b, int m) {
int r = 1;
while(b) {
if(b % 2) r = (long long) r * a % m;
a = (long long) a * a % m;
b /= 2;
}
return r;
}
int main() {
int n, m;
scanf("%d%d", &n, &m);
while(n--) {
int x;
scanf("%d", &x);
forbidden[x] = true;
}
#define n use_____m
for(int i = 0; i < m; ++i)
if(!forbidden[i])
which[my_gcd(i, m)].push_back(i);
if(forbidden[0])
which[m].push_back(0); // hack
for(int i = 1; i <= m; ++i)
if(!which[i].empty()) {
dp[i] = {0, 0};
for(int j = 1; j < i; ++j)
if(i % j == 0 && dp[j].first > 0)
dp[i] = max(dp[i], make_pair(dp[j].first, j));
dp[i].first += which[i].size();
}
vector<int> ans;
int x = m;
while(!which[x].empty()) {
for(int y : which[x])
ans.push_back(y);
x = dp[x].second;
}
reverse(ans.begin(), ans.end());
if(forbidden[0]) {
assert(!ans.empty());
ans.pop_back();
}
debug() << imie(ans);
int previous = 1;
printf("%d\n", (int) ans.size());
int cnt_coprime = 0;
for(int i = 2; i < m; ++i)
if(my_gcd(i, m) == 1)
++cnt_coprime;
for(int nxt : ans) {
if(nxt == 0) {
printf("0");
continue;
}
int a = previous / my_gcd(m, previous);
int b = nxt / my_gcd(m, nxt);
int print = (long long) b * my_pow(a, cnt_coprime, m) % m;
print = (long long) print * my_gcd(m, nxt) / my_gcd(m, previous) % m;
printf("%d ", print);
previous = nxt;
}
puts("");
}
import java.io.OutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.util.Arrays;
import java.io.BufferedWriter;
import java.io.Writer;
import java.io.OutputStreamWriter;
import java.util.InputMismatchException;
import java.io.IOException;
import java.util.ArrayList;
import java.io.InputStream;
/**
* Built using CHelper plug-in
* Actual solution is at the top
*/
public class Main {
public static void main(String[] args) {
InputStream inputStream = System.in;
OutputStream outputStream = System.out;
InputReader in = new InputReader(inputStream);
OutputWriter out = new OutputWriter(outputStream);
PrefixProductSequence solver = new PrefixProductSequence();
solver.solve(1, in, out);
out.close();
}
static class PrefixProductSequence {
public int[] div;
public boolean[] forbidden;
public ArrayList<Long> ans;
public int n;
public int m;
public void solve(int testNumber, InputReader in, OutputWriter out) {
n = in.nextInt();
m = in.nextInt();
forbidden = new boolean[m + 1];
for (int i = 0; i < n; i++) {
forbidden[in.nextInt()] = true;
}
int[] add = new int[m + 1];
for (int i = 0; i < m; i++) {
if (!forbidden[i]) {
int g = Utils.gcd(i, m);
add[m / g]++;
}
}
int[] arr = new int[m + 1];
div = new int[m + 1];
Arrays.fill(arr, 1);
Arrays.setAll(div, x -> x);
for (int i = 2; i <= m; i++) {
arr[i] += add[i];
for (int j = i + i; j <= m; j += i) {
if (arr[i] > arr[j]) {
arr[j] = arr[i];
div[j] = j / i;
}
}
}
ans = new ArrayList<>();
solve(1, 1);
out.println(ans.size());
boolean first = true;
for (long x : ans) {
if (!first) out.print(" ");
out.print(x);
first = false;
}
out.println();
}
public void solve(int cmult, long mm) {
if (cmult == m) {
if (!forbidden[0]) {
ans.add(0L);
}
return;
}
int prev = 1;
boolean has = false;
for (int i = 1; i < m / cmult; i++) {
if (!forbidden[i * cmult] && Utils.gcd(m / cmult, i) == 1) {
long x = Utils.inv(prev, m / cmult) * i % m;
if (!has) {
has = true;
x = x * mm % m;
}
ans.add(x);
prev = i;
}
}
long nmm = Utils.inv(prev, m / cmult) * div[m / cmult] % m;
if (!has) nmm = nmm * mm % m;
solve(cmult * div[m / cmult], nmm);
}
}
static class OutputWriter {
private final PrintWriter writer;
public OutputWriter(OutputStream outputStream) {
writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(outputStream)));
}
public OutputWriter(Writer writer) {
this.writer = new PrintWriter(writer);
}
public void print(Object... objects) {
for (int i = 0; i < objects.length; i++) {
if (i != 0) {
writer.print(' ');
}
writer.print(objects[i]);
}
}
public void println() {
writer.println();
}
public void close() {
writer.close();
}
public void print(long i) {
writer.print(i);
}
public void println(int i) {
writer.println(i);
}
}
static class InputReader {
private InputStream stream;
private byte[] buf = new byte[1024];
private int curChar;
private int numChars;
public InputReader(InputStream stream) {
this.stream = stream;
}
public int read() {
if (this.numChars == -1) {
throw new InputMismatchException();
} else {
if (this.curChar >= this.numChars) {
this.curChar = 0;
try {
this.numChars = this.stream.read(this.buf);
} catch (IOException var2) {
throw new InputMismatchException();
}
if (this.numChars <= 0) {
return -1;
}
}
return this.buf[this.curChar++];
}
}
public int nextInt() {
int c;
for (c = this.read(); isSpaceChar(c); c = this.read()) {
;
}
byte sgn = 1;
if (c == 45) {
sgn = -1;
c = this.read();
}
int res = 0;
while (c >= 48 && c <= 57) {
res *= 10;
res += c - 48;
c = this.read();
if (isSpaceChar(c)) {
return res * sgn;
}
}
throw new InputMismatchException();
}
public static boolean isSpaceChar(int c) {
return c == 32 || c == 10 || c == 13 || c == 9 || c == -1;
}
}
static class Utils {
public static long inv(long N, long M) {
long x = 0, lastx = 1, y = 1, lasty = 0, q, t, a = N, b = M;
while (b != 0) {
q = a / b;
t = a % b;
a = b;
b = t;
t = x;
x = lastx - q * x;
lastx = t;
t = y;
y = lasty - q * y;
lasty = t;
}
return (lastx + M) % M;
}
public static int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
}
}
// vvvvvvvvvvvvvvvvv Library code start
#include <array>
#define NDEBUG
NDEBUG
#include <algorithm>
#include <cassert>
#include <cstring>
#include <functional>
#include <iomanip>
#include <iostream>
#include <map>
#include <set>
#include <sstream>
#include <string>
#include <tuple>
#include <unordered_map>
#include <unordered_set>
#include <vector>
#include <memory>
#include <queue>
#include <random>
#define forn(t, i, n) for (t i = 0; i < (n); ++i)
#define rforn(t, i, n) for (t i = (n) - 1; i >= 0; --i)
#define all(c) c.begin(), c.end()
using namespace std;
/// caide keep
bool __hack = std::ios::sync_with_stdio(false);
/// caide keep
auto __hack1 = cin.tie(nullptr);
// Section with adoption of array and vector algorithms.
// 32 bit ints (sum LSB + MSB == 32)
// TODO: Section with some container algorithms
#define ENABLE_IF(e) typename enable_if<e>::type* = nullptr
namespace template_util {
template<class T>
constexpr T min(T a, T b) {
return a < b ? a : b;
}
constexpr int bytecount(uint64_t x) {
return x ? 1 + bytecount(x >> 8) : 0;
}
/// caide keep
template<int N>
struct bytetype {
typedef uint64_t type;
};
/// caide keep
template<>
struct bytetype<4> {
typedef uint32_t type;
};
/// caide keep
template<>
struct bytetype<3> {
};
/// caide keep
template<>
struct bytetype<2> {
};
/// caide keep
template<>
struct bytetype<1> {
typedef uint8_t type;
};
/// caide keep
template<>
struct bytetype<0> {
typedef uint8_t type;
};
/// caide keep
template<uint64_t N>
struct minimal_uint : bytetype<bytecount(N)> {
};
}
template<class T>
T next(istream& in) {
T ret;
in >> ret;
return ret;
}
template<class T>
vector<T> next_vector(istream& in, size_t n) {
vector<T> ret(n);
for (size_t i = 0; i < n; ++i) {
ret[i] = next<T>(in);
}
return ret;
}
#define dbg(...) ;
/*
TODOs:
cache invs
primitive root
discrete log
tests!!!
*/
namespace mod_impl {
/// caide keep
template <class T>
constexpr inline T mod(T MOD) {
return MOD;
}
/// caide keep
template <class T>
constexpr inline T mod(T* MOD) {
return *MOD;
}
/// caide keep
template <class T>
constexpr inline T max_mod(T MOD) {
return MOD - 1;
}
/// caide keep
template <class T>
constexpr inline T max_mod(T*) {
return numeric_limits<T>::max() - 1;
}
constexpr inline uint64_t combine_max_sum(uint64_t a, uint64_t b) {
return a > ~b ? 0 : a + b;
}
constexpr inline uint64_t combine_max_mul(uint64_t a, uint64_t b) {
return a > numeric_limits<uint64_t>::max() / b ? 0 : a * b;
}
/// caide keep
template <class T>
constexpr inline uint64_t next_divisible(T mod, uint64_t max) {
return max % mod == 0 ? max : combine_max_sum(max, mod - max % mod);
}
/// caide keep
template <class T>
constexpr inline uint64_t next_divisible(T*, uint64_t) {
return 0;
}
//caide keep
constexpr int IF_THRESHOLD = 2;
template <class T, T MOD_VALUE, uint64_t MAX,
class RET = typename template_util::minimal_uint<max_mod(MOD_VALUE)>::type,
ENABLE_IF(MAX <= max_mod(MOD_VALUE) && !is_pointer<T>::value)>
inline RET smart_mod(typename template_util::minimal_uint<MAX>::type value) {
return value;
}
template <class T, T MOD_VALUE, uint64_t MAX,
class RET = typename template_util::minimal_uint<max_mod(MOD_VALUE)>::type,
ENABLE_IF(max_mod(MOD_VALUE) < MAX && MAX <= IF_THRESHOLD * max_mod(MOD_VALUE) && !is_pointer<T>::value)>
inline RET smart_mod(typename template_util::minimal_uint<MAX>::type value) {
while (value >= mod(MOD_VALUE)) {
value -= mod(MOD_VALUE);
}
return (RET)value;
}
template <class T, T MOD_VALUE, uint64_t MAX,
class RET = typename template_util::minimal_uint<max_mod(MOD_VALUE)>::type,
ENABLE_IF(IF_THRESHOLD * max_mod(MOD_VALUE) < MAX || is_pointer<T>::value)>
inline RET smart_mod(typename template_util::minimal_uint<MAX>::type value) {
return (RET)(value % mod(MOD_VALUE));
}
}
#define MOD mod_impl::mod(MOD_VALUE)
#define MAX_MOD mod_impl::max_mod(MOD_VALUE)
struct DenormTag {};
template <class T, T MOD_VALUE, uint64_t MAX = MAX_MOD, ENABLE_IF(MAX_MOD >= 2)>
struct ModVal {
typedef typename template_util::minimal_uint<MAX>::type storage;
storage value;
/// caide keep
inline ModVal(): value(0) {
assert(MOD >= 2);
}
inline ModVal(storage v, DenormTag): value(v) {
assert(MOD >= 2);
assert(v <= MAX);
};
inline operator ModVal<T, MOD_VALUE>() {
return {v(), DenormTag()};
};
explicit inline operator uint64_t() const {
return v();
}
typename template_util::minimal_uint<mod_impl::max_mod(MOD_VALUE)>::type v() const {
return mod_impl::smart_mod<T, MOD_VALUE, MAX>(value);
}
};
template <class T, T MOD_VALUE, uint64_t MAX,
uint64_t NEW_MAX = mod_impl::next_divisible(MOD_VALUE, MAX),
ENABLE_IF(NEW_MAX != 0),
class Ret = ModVal<T, MOD_VALUE, NEW_MAX>>
inline Ret operator-(const ModVal<T, MOD_VALUE, MAX>& o) {
static_assert(NEW_MAX <= numeric_limits<typename Ret::storage>::max(), "bad unary minus template");
assert(NEW_MAX % MOD == 0 && o.value <= NEW_MAX);
return {typename Ret::storage(NEW_MAX - o.value), DenormTag()};
}
template <class T, T MOD_VALUE, uint64_t MAX1, uint64_t MAX2,
uint64_t NEW_MAX = mod_impl::combine_max_sum(MAX1, MAX2),
ENABLE_IF(NEW_MAX != 0), class Ret = ModVal<T, MOD_VALUE, NEW_MAX>>
inline Ret operator+(ModVal<T, MOD_VALUE, MAX1> o1, ModVal<T, MOD_VALUE, MAX2> o2) {
return {typename Ret::storage(typename Ret::storage() + o1.value + o2.value), DenormTag()};
}
template <class T, T MOD_VALUE, uint64_t MAX1, uint64_t MAX2,
uint64_t NEW_MAX = mod_impl::combine_max_mul(MAX1, MAX2),
ENABLE_IF(NEW_MAX != 0), class Ret = ModVal<T, MOD_VALUE, NEW_MAX>>
inline Ret operator*(ModVal<T, MOD_VALUE, MAX1> o1, ModVal<T, MOD_VALUE, MAX2> o2) {
return {typename Ret::storage(typename Ret::storage(1) * o1.value * o2.value), DenormTag()};
}
template <class T, T MOD_VALUE, uint64_t MAX1, uint64_t MAX2,
uint64_t NEW_MAX = mod_impl::combine_max_mul(MAX1, MAX2),
uint64_t NEW_MAX1 = mod_impl::combine_max_mul(MAX_MOD, template_util::min(MAX1, MAX2)),
ENABLE_IF(NEW_MAX == 0 && NEW_MAX1 != 0 && MAX1 <= MAX2),
class Ret = ModVal<T, MOD_VALUE, mod_impl::combine_max_mul(MAX1, MAX_MOD)>>
inline Ret operator*(const ModVal<T, MOD_VALUE, MAX1>& o1, const ModVal<T, MOD_VALUE, MAX2>& o2) {
return {typename Ret::storage(typename Ret::storage(1) * o1.value * o2.v()), DenormTag()};
}
template <class T, T MOD_VALUE, uint64_t MAX1, uint64_t MAX2,
uint64_t NEW_MAX = mod_impl::combine_max_mul(MAX1, MAX2),
uint64_t NEW_MAX1 = mod_impl::combine_max_mul(MAX_MOD, template_util::min(MAX1, MAX2)),
ENABLE_IF(NEW_MAX == 0 && NEW_MAX1 != 0 && MAX2 < MAX1),
class Ret = ModVal<T, MOD_VALUE, mod_impl::combine_max_mul(MAX_MOD, MAX2)>>
inline Ret operator*(const ModVal<T, MOD_VALUE, MAX1>& o1, const ModVal<T, MOD_VALUE, MAX2>& o2) {
return {typename Ret::storage(typename Ret::storage(1) * o1.v() * o2.value), DenormTag()};
}
template <class T, T MOD_VALUE, uint64_t MAX1, uint64_t MAX2>
inline auto operator-(const ModVal<T, MOD_VALUE, MAX1>& lhs, const ModVal<T, MOD_VALUE, MAX2>& rhs) -> decltype(lhs + (-rhs)) {
return lhs + (-rhs);
}
template <class T, T MOD_VALUE, uint64_t MAX>
inline ModVal<T, MOD_VALUE>& operator+=(ModVal<T, MOD_VALUE>& lhs, const ModVal<T, MOD_VALUE, MAX>& rhs) {
lhs = lhs + rhs;
return lhs;
}
template <class T, T MOD_VALUE, uint64_t MAX>
inline ModVal<T, MOD_VALUE>& operator-=(ModVal<T, MOD_VALUE>& lhs, const ModVal<T, MOD_VALUE, MAX>& rhs) {
lhs = lhs - rhs;
return lhs;
}
template <class T, T MOD_VALUE, uint64_t MAX1, uint64_t MAX2>
inline bool operator!=(const ModVal<T, MOD_VALUE, MAX1>& lhs, const ModVal<T, MOD_VALUE, MAX2>& rhs) {
return lhs.v() != rhs.v();
}
template <class T, T MOD_VALUE, class MOD_TYPE>
struct ModCompanion {
typedef MOD_TYPE mod_type;
typedef ModVal<mod_type, MOD_VALUE> type;
template <uint64_t C>
inline static constexpr ModVal<mod_type, MOD_VALUE, C> c() {
return {C, DenormTag()};
};
template <uint64_t MAX = numeric_limits<uint64_t>::max()>
inline static ModVal<mod_type, MOD_VALUE, MAX> wrap(uint64_t x) {
assert(x <= MAX);
return {typename ModVal<mod_type, MOD_VALUE, MAX>::storage(x), DenormTag()};
};
template <uint64_t MAX, ENABLE_IF(!is_pointer<T>::value && MAX <= MAX_MOD)>
inline static ModVal<mod_type, MOD_VALUE> inv(const ModVal<mod_type, MOD_VALUE, MAX>& x) {
if (x.value == 1) {
return c<1>();
}
return -(wrap<MAX_MOD / 2>(MOD / x.value) * inv(wrap<MAX>(MOD % x.value)));
};
};
#undef MOD
#undef MAX_MOD
template <uint64_t MOD_VALUE>
struct Mod : ModCompanion<uint64_t, MOD_VALUE, typename template_util::minimal_uint<MOD_VALUE>::type> {
template<uint64_t VAL>
static constexpr uint64_t literal_builder() {
return VAL;
}
template<uint64_t VAL, char DIGIT, char... REST>
static constexpr uint64_t literal_builder() {
return literal_builder<(10 * VAL + DIGIT - '0') % MOD_VALUE, REST...>();
}
};
#define REGISTER_MOD_LITERAL(mod, suffix) \
template <char... DIGITS> mod::type operator "" _##suffix() { \
return mod::c<mod::literal_builder<0, DIGITS...>()>(); \
}
// ^^^^^^^^^^^^^^^^^ Library code end
using md = Mod<1000000007>;
using mt = md::type;
REGISTER_MOD_LITERAL(md, mod)
using Val = tuple<int, mt, mt>;
mt pow2s[1000001], powInv2s[1000001];
mt pow2(int p) {
return p < 0 ? powInv2s[-p] : pow2s[p];
}
Val mul(Val a, Val b) {
const mt p2a = pow2(get<0>(a));
const mt p2b = pow2(get<0>(b));
return Val{get<0>(a) + get<0>(b), p2a * get<1>(b) + get<1>(a) * p2b, p2a * get<2>(b) + 2_mod * get<1>(a) * get<1>(b) + get<2>(a) * p2b};
}
Val inv(Val a) {
Val b;
get<0>(b) = -get<0>(a);
const mt p2b = pow2(get<0>(b));
get<1>(b) = -p2b * (get<1>(a) * p2b);
get<2>(b) = -p2b * (2_mod * get<1>(a) * get<1>(b) + get<2>(a) * p2b);
return b;
}
Val d[1000000][7];
mt dSum[1000000][7];
void solve(istream& in, ostream& out) {
pow2s[0] = powInv2s[0] = 1_mod;
mt inv2 = md::inv(2_mod);
forn (int, i, 1000000) {
pow2s[i + 1] = pow2s[i] * 2_mod;
powInv2s[i + 1] = powInv2s[i] * inv2;
}
int n = next<int>(in);
auto as = next_vector<int>(in, n);
sort(all(as));
uint64_t ans = 0;
int add[1 << 6];
forn (int, mask, 1 << 6) {
add[mask] = 0;
int mask1 = mask;
forn (int, it, 6) {
add[mask] = add[mask] * 10 + (mask1 & 1);
mask1 /= 2;
}
}
int asIt = n - 1;
rforn (int, x, 1000000) {
int badMask = 0;
int x1 = x;
forn (int, it, 6) {
badMask = 2 * badMask + (x1 % 10 == 9 ? 1 : 0);
x1 /= 10;
}
d[x][0] = Val{0, 0_mod, 0_mod};
dSum[x][0] = 0_mod;
forn (int, bit, 6) {
d[x][bit + 1] = d[x][bit];
dSum[x][bit + 1] = dSum[x][bit];
if (!(badMask & (1 << bit))) {
d[x][bit + 1] = mul(d[x][bit + 1], inv(d[x + add[1 << bit]][bit]));
dSum[x][bit + 1] -= dSum[x + add[1 << bit]][bit];
}
}
auto val = inv(d[x][6]);
while (asIt >= 0 && as[asIt] == x) {
--asIt;
val = mul(val, Val{1, md::wrap(x), md::wrap(1ULL * x * x)});
}
auto sum = get<2>(val) + dSum[x][6];
forn (int, bit, 6) {
d[x][bit] = mul(d[x][bit], val);
dSum[x][bit] += get<2>(val);
}
if (sum != 0_mod) {
dbg(x, sum, x * uint64_t(sum));
ans ^= x * uint64_t(sum);
}
}
out << ans << endl;
}
int main() {
solve(cin, cout);
return 0;
}
import java.io.OutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.io.BufferedWriter;
import java.io.Writer;
import java.io.OutputStreamWriter;
import java.util.InputMismatchException;
import java.io.IOException;
import java.io.InputStream;
/**
* Built using CHelper plug-in
* Actual solution is at the top
*/
public class Main {
public static void main(String[] args) {
InputStream inputStream = System.in;
OutputStream outputStream = System.out;
InputReader in = new InputReader(inputStream);
OutputWriter out = new OutputWriter(outputStream);
MinAddition solver = new MinAddition();
solver.solve(1, in, out);
out.close();
}
static class MinAddition {
public int[] pow10 = {1, 10, 100, 1000, 10000, 100000, 1000000};
public int MAXN = 1000000;
public int LOG = 6;
public int mod = 1000000007;
public void solve(int testNumber, InputReader in, OutputWriter out) {
int n = in.nextInt();
int[] freq = new int[MAXN];
int[] sum = new int[MAXN];
int[] sum2 = new int[MAXN];
int[] pow2 = new int[n + 1];
pow2[0] = 1;
for (int i = 1; i <= n; i++) pow2[i] = (pow2[i - 1] << 1) % mod;
for (int i = 0; i < n; i++) {
int a = in.nextInt();
freq[a]++;
sum[a] += a;
if (sum[a] >= mod) sum[a] -= mod;
int x = (int) (1L * a * a % mod);
sum2[a] += x;
if (sum2[a] >= mod) sum2[a] -= mod;
}
int[] mod10 = new int[MAXN];
for (int i = 0; i < 10; i++) mod10[i] = i;
for (int i = 10; i < MAXN; i++) mod10[i] = mod10[i - 10];
for (int level = LOG - 1; level >= 0; level--) {
for (int i = MAXN - 1; i >= 0; i--) {
int d = mod10[i / pow10[level]];
if (d > 0) {
int p = i - pow10[level];
freq[p] += freq[i];
sum[p] += sum[i];
if (sum[p] >= mod) sum[p] -= mod;
sum2[p] += sum2[i];
if (sum2[p] >= mod) sum2[p] -= mod;
}
}
}
for (int i = 0; i < MAXN; i++) {
int sdiff = (int) ((1L * sum[i] * sum[i] + mod - sum2[i]) % mod);
int ssame = sum2[i];
int g = 0;
if (freq[i] >= 1)
g += (int) (1L * ssame * pow2[freq[i] - 1] % mod);
if (freq[i] >= 2)
g += (int) (1L * sdiff * pow2[freq[i] - 2] % mod);
while (g >= mod) g -= mod;
freq[i] = g;
}
for (int level = 0; level < LOG; level++) {
for (int i = 0; i < MAXN; i++) {
int d = mod10[i / pow10[level]];
if (d + 1 < 10) {
int p = i + pow10[level];
freq[i] -= freq[p];
if (freq[i] < 0) freq[i] += mod;
}
}
}
long s = 0;
for (int i = 0; i < MAXN; i++) {
s ^= 1L * i * freq[i];
}
out.println(s);
}
}
static class OutputWriter {
private final PrintWriter writer;
public OutputWriter(OutputStream outputStream) {
writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(outputStream)));
}
public OutputWriter(Writer writer) {
this.writer = new PrintWriter(writer);
}
public void close() {
writer.close();
}
public void println(long i) {
writer.println(i);
}
}
static class InputReader {
private InputStream stream;
private byte[] buf = new byte[1024];
private int curChar;
private int numChars;
public InputReader(InputStream stream) {
this.stream = stream;
}
public int read() {
if (this.numChars == -1) {
throw new InputMismatchException();
} else {
if (this.curChar >= this.numChars) {
this.curChar = 0;
try {
this.numChars = this.stream.read(this.buf);
} catch (IOException var2) {
throw new InputMismatchException();
}
if (this.numChars <= 0) {
return -1;
}
}
return this.buf[this.curChar++];
}
}
public int nextInt() {
int c;
for (c = this.read(); isSpaceChar(c); c = this.read()) {
;
}
byte sgn = 1;
if (c == 45) {
sgn = -1;
c = this.read();
}
int res = 0;
while (c >= 48 && c <= 57) {
res *= 10;
res += c - 48;
c = this.read();
if (isSpaceChar(c)) {
return res * sgn;
}
}
throw new InputMismatchException();
}
public static boolean isSpaceChar(int c) {
return c == 32 || c == 10 || c == 13 || c == 9 || c == -1;
}
}
}
// vvvvvvvvvvvvvvvvv Library code start
#define NDEBUG
NDEBUG
#include <algorithm>
#include <array>
#include <cassert>
#include <cstring>
#include <functional>
#include <iomanip>
#include <iostream>
#include <map>
#include <set>
#include <sstream>
#include <string>
#include <tuple>
#include <unordered_map>
#include <unordered_set>
#include <vector>
#include <memory>
#include <queue>
#include <random>
#define forn(t, i, n) for (t i = 0; i < (n); ++i)
#define foran(t, i, a, n) for (t i = (a); i < (n); ++i)
using namespace std;
/// caide keep
bool __hack = std::ios::sync_with_stdio(false);
/// caide keep
auto __hack1 = cin.tie(nullptr);
template<class T>
inline T mn(T arg) {
return arg;
}
template<class T, class... Args>
inline bool rmx(T &to, Args... args) {
auto v = mn(args...);
if (to < v) {
to = v;
return true;
}
return false;
}
// Section with adoption of array and vector algorithms.
// 32 bit ints (sum LSB + MSB == 32)
// TODO: Section with some container algorithms
namespace template_util {
constexpr int bytecount(uint64_t x) {
return x ? 1 + bytecount(x >> 8) : 0;
}
/// caide keep
template<int N>
struct bytetype {
};
/// caide keep
template<>
struct bytetype<4> {
};
/// caide keep
template<>
struct bytetype<3> {
};
/// caide keep
template<>
struct bytetype<2> {
};
/// caide keep
template<>
struct bytetype<1> {
};
/// caide keep
template<>
struct bytetype<0> {
};
/// caide keep
template<uint64_t N>
struct minimal_uint : bytetype<bytecount(N)> {
};
}
template<class T>
T next(istream& in) {
T ret;
in >> ret;
return ret;
}
// ^^^^^^^^^^^^^^^^^ Library code end
int tr[1000][3];
int l[1000], r[1000];
bool col[1000];
int ans[2000];
tuple<int, int, int> chooseDfs(int total, int i, int p = -1) {
int size = 1, best = -1, bestSize = 1000000000, maxSize = 0;
forn (int, e, 3) {
int j = tr[i][e];
if (j != p && j >= 0 && !col[j]) {
auto r1 = chooseDfs(total, j, i);
if (get<1>(r1) < bestSize) {
best = get<0>(r1);
bestSize = get<1>(r1);
}
size += get<2>(r1);
rmx(maxSize, get<2>(r1));
}
}
rmx(maxSize, total - size);
if (maxSize < bestSize) {
best = i;
bestSize = maxSize;
}
return tuple<int, int, int>{best, bestSize, size};
}
int sizeDfs(int i, int p = -1) {
auto r = 1;
forn (int, e, 3) {
int j = tr[i][e];
if (j != p && j >= 0 && !col[j]) {
r += sizeDfs(j, i);
}
}
return r;
}
void ansDfs(int n, int i) {
forn (int, e, 2) {
if (tr[i][e] >= 0) {
ansDfs(n, tr[i][e]);
}
ans[tr[i][e] < 0 ? -2 - tr[i][e] : n + tr[i][e]] = n + i + 1;
}
}
void solve(istream& in, ostream& out) {
auto q = [&](int a, int b, int c) {
out << a + 1 << " " << b + 1 << " " << c + 1 << endl;
string s = next<string>(in);
if (s == "X") {
return 2;
} else if (s == "Y") {
return 1;
} else if (s == "Z") {
return 0;
} else {
throw 42;
}
};
int n = next<int>(in);
memset(tr, -1, sizeof(tr));
tr[0][0] = -2;
tr[0][1] = -3;
l[0] = 0;
r[0] = 1;
foran (int, i, 2, n) {
memset(col, 0, sizeof(col));
int x = 0;
while (true) {
x = get<0>(chooseDfs(sizeDfs(x), x));
int e = q(l[x], r[x], i);
if (tr[x][e] < 0 || col[tr[x][e]]) {
if (tr[x][e] >= 0) {
forn (int, e1, 3) {
if (tr[tr[x][e]][e1] == x) {
tr[tr[x][e]][e1] = i - 1;
}
}
}
tr[i - 1][e] = tr[x][e];
tr[x][e] = i - 1;
tr[i - 1][e == 0 ? 1 : 0] = -2 - i;
tr[i - 1][e == 2 ? 1 : 2] = x;
l[i - 1] = tr[i - 1][0] < 0 ? -2 - tr[i - 1][0] : l[tr[i - 1][0]];
r[i - 1] = tr[i - 1][1] < 0 ? -2 - tr[i - 1][1] : r[tr[i - 1][1]];
break;
}
col[x] = true;
x = tr[x][e];
}
}
int r = 0;
while (tr[r][2] != -1) {
r = tr[r][2];
}
ans[n + r] = -1;
ansDfs(n, r);
out << "-1\n";
forn (int, i, 2 * n - 1) {
out << ans[i] << " ";
}
out << "\n";
}
int main() {
solve(cin, cout);
return 0;
}
import java.io.OutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.io.BufferedWriter;
import java.io.Writer;
import java.io.OutputStreamWriter;
import java.util.InputMismatchException;
import java.io.IOException;
import java.io.InputStream;
/**
* Built using CHelper plug-in
* Actual solution is at the top
*/
public class Main {
public static void main(String[] args) {
InputStream inputStream = System.in;
OutputStream outputStream = System.out;
InputReader in = new InputReader(inputStream);
OutputWriter out = new OutputWriter(outputStream);
ForgottenTree solver = new ForgottenTree();
solver.solve(1, in, out);
out.close();
}
static class ForgottenTree {
public InputReader in;
public OutputWriter out;
public int nidx;
public int n;
public int[] par;
public void solve(int testNumber, InputReader in, OutputWriter out) {
this.in = in;
this.out = out;
n = in.nextInt();
nidx = n;
ForgottenTree.Node root = new ForgottenTree.Node(0);
ForgottenTree.Node.cgen = 0;
for (int i = 1; i < n; i++) {
ForgottenTree.Node.cgen++;
root.getLeaves();
root = insert(root, i);
}
out.println(-1);
par = new int[2 * n - 1];
dfs(root, -2);
out.println(par);
}
public String ask(int a, int b, int c) {
out.println((a + 1) + " " + (b + 1) + " " + (c + 1));
out.flush();
String ret = in.next();
if (ret.equals("-1")) System.exit(0);
return ret;
}
public void dfs(ForgottenTree.Node root, int p) {
par[root.label] = p + 1;
if (root.lchild != null) {
dfs(root.lchild, root.label);
dfs(root.rchild, root.label);
}
}
public ForgottenTree.Node insert(ForgottenTree.Node root, int label) {
if (!root.active()) {
return add(root, label);
}
root.dfs();
if (root.lchild == null) {
return add(root, label);
}
int curleaves = root.nleaves;
if (curleaves <= 1) {
int nnodes = 0;
ForgottenTree.Node cur = root;
while (!cur.isLeaf()) {
nnodes++;
if (cur.lchild.active()) cur = cur.lchild;
else cur = cur.rchild;
}
cur = root;
int depth = 0;
while (2 * (depth + 1) < nnodes) {
if (cur.lchild.active()) cur = cur.lchild;
else cur = cur.rchild;
depth++;
}
return process(root, cur, label);
}
ForgottenTree.Node cur = root;
while (true) {
if (cur.lchild == null) {
if (cur.par == null) {
return add(cur, label);
}
if (cur.which == 0) {
cur.par.setChild(0, add(cur, label));
return root;
} else {
cur.par.setChild(1, add(cur, label));
return root;
}
}
int x1 = cur.lchild.active() ? cur.lchild.nleaves : 0;
int x2 = cur.rchild.active() ? cur.rchild.nleaves : 0;
if (x1 * 2 > curleaves) {
cur = cur.lchild;
continue;
}
if (x2 * 2 > curleaves) {
cur = cur.rchild;
continue;
}
return process(root, cur, label);
}
}
public ForgottenTree.Node process(ForgottenTree.Node root, ForgottenTree.Node cur, int label) {
String s = ask(cur.x, cur.y, label);
switch (s) {
case "X":
if (cur.par == null) {
return add(cur, label);
}
cur.disable();
return insert(root, label);
case "Y":
cur.setChild(1, insert(cur.rchild, label));
return root;
case "Z":
cur.setChild(0, insert(cur.lchild, label));
return root;
default:
throw new RuntimeException();
}
}
public ForgottenTree.Node add(ForgottenTree.Node cnode, int label) {
ForgottenTree.Node add = new ForgottenTree.Node(nidx++);
add.setChild(0, cnode);
add.setChild(1, new ForgottenTree.Node(label));
return add;
}
static class Node {
public static int cgen;
public int x;
public int y;
public int label;
public int gen;
public int nleaves;
public int which;
public ForgottenTree.Node lchild;
public ForgottenTree.Node rchild;
public ForgottenTree.Node par;
public Node(int label) {
this.lchild = null;
this.rchild = null;
this.par = null;
this.which = 0;
this.label = label;
this.gen = 0;
this.nleaves = 1;
}
public boolean active() {
return gen < cgen;
}
public void disable() {
this.gen = cgen;
}
public boolean isLeaf() {
return lchild == null || (!lchild.active() && !rchild.active());
}
public void setChild(int which, ForgottenTree.Node x) {
if (which == 0) {
this.lchild = x;
} else {
this.rchild = x;
}
x.par = this;
x.which = which;
}
public void dfs() {
if (isLeaf()) {
this.nleaves = 1;
return;
}
this.nleaves = 0;
if (lchild.active()) {
lchild.dfs();
this.nleaves += lchild.nleaves;
}
if (rchild.active()) {
rchild.dfs();
this.nleaves += rchild.nleaves;
}
}
public void getLeaves() {
if (lchild == null) {
this.x = this.y = label;
return;
}
lchild.getLeaves();
rchild.getLeaves();
this.x = lchild.x;
this.y = rchild.x;
}
}
}
static class InputReader {
private InputStream stream;
private byte[] buf = new byte[1024];
private int curChar;
private int numChars;
public InputReader(InputStream stream) {
this.stream = stream;
}
public int read() {
if (this.numChars == -1) {
throw new InputMismatchException();
} else {
if (this.curChar >= this.numChars) {
this.curChar = 0;
try {
this.numChars = this.stream.read(this.buf);
} catch (IOException var2) {
throw new InputMismatchException();
}
if (this.numChars <= 0) {
return -1;
}
}
return this.buf[this.curChar++];
}
}
public int nextInt() {
int c;
for (c = this.read(); isSpaceChar(c); c = this.read()) {
;
}
byte sgn = 1;
if (c == 45) {
sgn = -1;
c = this.read();
}
int res = 0;
while (c >= 48 && c <= 57) {
res *= 10;
res += c - 48;
c = this.read();
if (isSpaceChar(c)) {
return res * sgn;
}
}
throw new InputMismatchException();
}
public String next() {
int c;
while (isSpaceChar(c = this.read())) {
;
}
StringBuilder result = new StringBuilder();
result.appendCodePoint(c);
while (!isSpaceChar(c = this.read())) {
result.appendCodePoint(c);
}
return result.toString();
}
public static boolean isSpaceChar(int c) {
return c == 32 || c == 10 || c == 13 || c == 9 || c == -1;
}
}
static class OutputWriter {
private final PrintWriter writer;
public OutputWriter(OutputStream outputStream) {
writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(outputStream)));
}
public OutputWriter(Writer writer) {
this.writer = new PrintWriter(writer);
}
public void print(Object... objects) {
for (int i = 0; i < objects.length; i++) {
if (i != 0) {
writer.print(' ');
}
writer.print(objects[i]);
}
}
public void print(int[] array) {
for (int i = 0; i < array.length; i++) {
if (i != 0) {
writer.print(' ');
}
writer.print(array[i]);
}
}
public void println(int[] array) {
print(array);
writer.println();
}
public void println(Object... objects) {
print(objects);
writer.println();
}
public void close() {
writer.close();
}
public void flush() {
writer.flush();
}
public void println(int i) {
writer.println(i);
}
}
}
Hello!
The round 2 of VK Cup 2017 will take place on April 16 at 18:35 MSK (check your timezone here), along with separate div1 and div2 Codeforces Round #409. The contest "VK Cup 2017 — Round 2" is for teams qualified from round 1. The top 100 teams will advance to the Round 3, while other ones will have one more chance in the Wild Card Round 2 later this month. Those who don't participate in the VK Cup can take part in the Codeforces Round #409 individually (problems will be available in English too). All three rounds last 2 hours, and all are rated.
The round would not be possible without the following people (in no particular order): KAN, Errichto, winger, AlexFetisov, LiChenKoh, xiaowuc1, MikeMirzayanov. Additionally, I thank VK company for sponsoring this contest.
As usual, the scoring distribution will be announced later.
UPD 1: The scoring distribution is as follows:
div2: 500 — 1000 — 1500 — 2000 — 2750
div1 and official round: 500 — 1000 — 1750 — 2250 — 2250
UPD 2: The tutorial is available here: http://codeforces.net/blog/entry/51598
Congratulations for the winners
Official round:
- LHiC, V--o_o--V
- I_love_Tanya_Romanova, enot110
- netman, andrew.volchek
- aid, ershov.stanislav
- MrDindows, Rubanenko
div 1:
div 2:
| Name |
|---|










