Hello Everyone.
I would like to invite you to participate in ACM Arabella 2017 which will be launched in GYM Friday 14/04/2017 14:00 UTC
You will be given 13 problem to solve in 5 hours, The contest difficulty is similar to Div2 Contests.
The problem-set were prepared by Hasan0540 , Hiasat , Motarack Reem , Az3ar abed.jaradat , Lvitsa and Ahmad Alkhaldi.
Good luck for everyone.










How do I register for this? I have never used the "Gym" function before.
It is very similar to regular Contests. Yet the registration button appears a little bit later (typically a few hours before the contest starts).
Thanks!
Any hint about problem E :\
If you are the first player then you can have this winning strategy:
You need to split the the squares into 2 groups each of the same size and whatever the other player does into a group, you are going to make a similar move into the other group till you win (similar to a nim game with 2 piles).
So if the game starts with an odd number, you can remove 3 squares in the middle to split the squares into 2 equal groups, and if the game starts with an even number you can remove 2 squares from the middle.
You will be able to use numbers 2, 3 only if the given number is greater than or equal to 4.
So the first player wins if the given number is 1 or is greater than or equal to 4, otherwise the second player will win.
Try to look for a strategy to follow that will always guarantee a player's victory.
the first player always wins when n ≥ 4.
if n is odd the first player will color 3 squares in the middle, after that the line will be separated into 2 identical lines, then any move the second player does on a line, the first will mimic it on the other line.
the same goes for when n is even, but coloring 2 squares instead.
you can manually solve the problem for n ≤ 3.
Can someone explain the approach for problem A.
Since it's require i < j < k where s[j] equals to 1 then the problem is equivalent to number of pairs where i < j and number of ones between them is odd
We also need to satisfy j-i>=2.Also we need to eliminate subarrays with exactly 1 one and which are beginning or ending with 1.
@shubhamgoyal__ What about the case "111"? There is clearly one subarray that works, "111", which begins AND ends with a "1".
EDIT: Oh, I see, it must have both those conditions satisfied for deletion from the total count...
How to solve problem L?
The amount of water could be stored between all walls is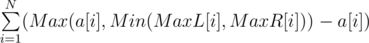 .
.
Where MaxR[i] is the maximum number of blocks in a wall comes from the right side and MaxL[i] is the maximum number of blocks in a wall comes from the left side.
So now we will have 2 arrays :
a which stores the number of blocks in each wall.
b which stores the number of blocks of each wall + the amount of water on top of each wall.
If we added the amount of water could be stored on each wall we can see that the numbers we got are sorted in an ascending order until we reach the maximum value then they become sorted in a descending order.
Queries :
if the query was of the first type then we should print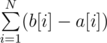 .
.
if the query was of the second type, we will have on these conditions :
1- : after increasing a[x] it is still smaller than or equal to b[x], in this case we will just update a[x].
2- : increasing the maximum value, in this case we should update b[index of the maximum value] and a[index of the maximum value].
3- : after increasing a[x] it becomes larger than the maximum value, in this case we should update all the values between x and the index of the maximum value in array b and make it equal to the maximum value, after updating we should change the maximum value into a[x] then update b[x] and make it equal to a[x].
4- :after increasing a[x] it becomes larger than b[x] but still smaller than the maximum value, in this case we should update all values smaller than a[x] in array b in the range [x,index of the maximum value] to a[x] and because we know that values between x and index of the maximum value are sorted we can find the first value larger than a[x] (starting from x) and change all the values between x and the first value larger than a[x] in array b into a[x].
To update sum and get sum value in array b we can use segment tree with lazy propagation and we can use binary search to find the first value larger than a[x] in array b
Can someone give some hint on problem G?
used principle
Inclusion — Exclusion principle
Solution
Bruteforce all Subsets and check how many ways to chose rectangle that's the chosen subset inside it you can find number of ways depend on MinY,MaxY,MinX,MaxX of current subset
Thanks!
@Hiasat I tried using TSP Complexity (K*2^K) in my submission here (29608212), but I get TLE on the first case. Did I misunderstand your method, or do I need some kind of optimization?
UPD 1: I made another optimization (in addition to precomputing multiplications), where I precompute the bits turned on in a mask. The code here still TLEs on the first case.
UPD 2: Changing all of my variables to global ones gave me AC in about 3 seconds...
I know solution with complexity like O(K * (N + KlogK)). First, how to solve this problem: given matrix N*M with 0/1 cells, we need to count number of rectangles without 1-cells. It can be solved using stack in O(N * M).
So this task is similar but we have not more than 20 1-cells. In that task we visited every column for every row, but in this task we need to visit not more than K columns for every row. When we are iterating row we need to keep sorted by y array of 1-cells with x <= row. I think it is better than exponential solution.
Can you explain how this algorithm does the counting?
Let f[i][j] — count of such (x, y) x <= i, y <= j, there is no 1-cells in subrectangle (x, y, i, j). For example we know f[i][g] (let's call it x), next 1-cell is in column j.
How to count f[i][j] and add to answer sum of all f[i][s], g < s <= j? It is obvious that f[i][s] = f[i][s — 1] + h, so sum of them is sum_of(x + h * (s — g)) = x * d + h * sum_of(s — g) = x * d + h * (d * (d + 1)) / 2, f[i][j] = x + h * d.
Any hints about F? :/
I think we need to store 1e5 dynamic segment trees, each of them corresponds to one type of joke. Node of segtree will store cnt[3] and del value, where cnt0 — count of monkeys that haven't heard joke with type corresponding to this segtree, cnt1 — count of monkeys that fell off their chairs, cnt2 — count of monkeys that have heard joke, but they are sitting in chairs, del — count of delayed updates for range of this node. To update node we just need cnt2 += cnt1, cnt1 = cnt0, cnt0 = 0, ++ del (if node's range is fully included in query).
After all queries we need to find the answer. We'll make another segtree with range assigning. Now for each dynamic segment tree push all delayed values and for each leaf if it has range [l, r] with value 1 (monkeys in [l, r] fell out of their chairs) we'll assign [l, r] in our answer array a 1. Then answer is count of 1 in result array (we could use sweep line instead of segtree). Complexity is like O(Q * log N).
Yesss, finally someone is asking about the only problem I wrote :P
This problem can be solved after realizing the following observation:
the posture of the monkey depends entirely on the last joke he hears, regardless of his previous posture.
Case 1- last joke monkey hears is new, final posture will be on floor:
- if the monkey was on the floor, he will stay on the floor
- if the monkey was sitting up in his chair, he will fall on the floor.
Case 2- last joke monkey hears is old, final posture is sitting up:
- if monkey was on the floor, he will sit up
- if monkey was sitting up, he will stay sitting up
Therefore to conclude the final posture of the monkey, you only need to know two things: the last joke he heard, and if he heard it more than once.
Both can be done using combination of sets, vectors, and cumulative sum, or with segment tree if you so prefer. Pick your favourite implementation!
Can you give me some hints on problem M. I've tried unordered_map and binary search but both failed for me :( This is my binary search code: https://ideone.com/vrkOpV.
The verdict you're getting is Time Limit Exceeded, that means your program was too slow (it could still be correct!).
Looking at your code, the thing making your program slow is probably the usage of cin and cout, it's common knowledge that they're not the fastest when reading and printing input/output.
Instead, try using scanf and printf to read and print the variables.
If you're not already familiar with them, you can read about them here:
http://www.cplusplus.com/reference/cstdio/scanf/
http://www.cplusplus.com/reference/cstdio/printf/
Yeah but we can't use scanf with string in C++
Yes we can't.
Instead we can use a character array (for the problem I think the strings are at most 10 characters), so we can do it like
char s[11];.Reading a character array using scanf and then converting it into a string (if needed) is still much faster than reading a string using cin.
Didn't know that thank you so much