I have been trying to solve this question with MO's algorithm. but My solution was getting TLE. Please somebody share an approach, if it is possible to solve with MO's algorithm . Link to problem : http://codeforces.net/contest/588/problem/E
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.12.2024 12:22:56 (i1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










Auto comment: topic has been updated by papa-ka-para (previous revision, new revision, compare).
Keeping the set of people on the current path in a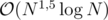 time complexity, which is unlikely to pass. In a set it is
time complexity, which is unlikely to pass. In a set it is 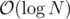 for inserting, deleting and finding the minimal a elements. However you insert and delete more often than you find the minimal elements.
for inserting, deleting and finding the minimal a elements. However you insert and delete more often than you find the minimal elements.
set<int>or similar structure will have aThere exists a data structure which lets you insert and delete elements in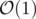 , while taking
, while taking 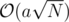 to find the minimal elements. For this, divide the range of legal values into
to find the minimal elements. For this, divide the range of legal values into  equal blocks and for each block keep a hash table containing all the added elements in that block. To insert or delete, simply access the relevant hash table, to find minimal, iterate through all possible elements while skipping the ranges where the hash table is empty. Using this, the complexity is
equal blocks and for each block keep a hash table containing all the added elements in that block. To insert or delete, simply access the relevant hash table, to find minimal, iterate through all possible elements while skipping the ranges where the hash table is empty. Using this, the complexity is 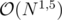
It is also worth noting that in the case of this problem, after you flatten the tree into an array, instead of dividing into blocks of cities, you should divide into blocks of
cities, you should divide into blocks of  people, otherwise Mo's algorithm won't optimize as intended.
people, otherwise Mo's algorithm won't optimize as intended.
This is still quite slow, the constant is large and hash-tables only support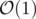 on average, not every time. I would prefer to use a method that uses
on average, not every time. I would prefer to use a method that uses 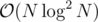 time. Centroid decomposition works really well here, HLD is not bad either.
time. Centroid decomposition works really well here, HLD is not bad either.
Hi, sorry for late reply.
I learnt something new, that you mentioned in second paragrah, and third paragraph. Thank you for your reply.
I will try it with centroid decomposition.