Hello, everyone.
I'm sorry for writing editorial too late.
I hope that you can use the commentary to solve the problem of s8pc or review the contest.
Please write comments where you do not understand, impressions, and discussions.

This is the square869120contest #4 (in AtCoder) editorial.
Writers were square1001 and E869120.

Since I think that there are also many people who have not yet seen the problem and forgotten it, I will attach a link to the problem statement.

A — Atcoder Handles

In this problem, the possible index of the handle name of Mr.X will be a "Range". (Example of "Range": {4,5,6,7}, {3,4,5,6,7,8,9,10})
Proof:

• The handle name of Mr.X doesn't include '?' — This means there is only one possibility of his name.
• If one of the others name (in the list) changes, the index of Mr.X will change no more than one.
• So, every index between "Minimum" to "Maximum" is possible.

For example:

 abcde -> zzzzz(changed)
 bbbbb
 ccccc
 ddddd
 Mr.X: cprpr 

In this example, Mr.X's index changed from 4 to 3.

Adittionally, The maximum and minimum value of Mr.X's index can find for this way:

• Minimum: When all characters of '?' in the list are 'z'.
• Maximum: When all characters of '?' in the list are 'a'.

Since possible index of the handle name of Mr.X is "Range", you can solve this problem with only minimum-value and maximum-value.

B — Buildings are Colorful

Let's consider the case of N = K.
You can solve this problem with greedy method if N = K is true. (a[i] is the height of building i)

 long long ret = 0, Y = 0;
 for (int i = 0; i < n; i++) {
  if (Y >= a[i]) { ret += ((Y + 1) — a[i]); Y++; } // When previous building (After change) is lower than this
  else { Y = a[i]; } // Else
 }
 //The answer is ret.
 

So, you can get 120 points in this way.

Let's think about "What buildings should be visible". (The number of should-visible buildings must be greater than K)
There are N buildings along the line, so you have to think only 2^N ways.

You can use greedy method to solve the following problem:

• You are given the index of buildings that should be visible.
• Find the minimum cost.

The greedy method is here:

 Let L be the maximum value of building's (that in front of this, After changed) height:
 If the building don't have to be visible, this building's height will not be increased.
 If the building have to be visible, this building's height will be max(This building's height,  L)
 

You can solve this problem (Max point) with brute-force method and greedy method.
The complexityis O(2^N).

C — Calendar 2

You can solve this problem in O(N) in BFS or DFS algorithm, but you can only get 100 points in this way.

Let's consider to split the calendar every M rows. (Because this calendar have Periodicity per M squares, if m in the problem statement is divided by 7, M will be m / 7)
"The calendar between i * M + 1-th row to (i + 1) * M-th row" and "The calendar between (i + 1) * M + 1-th row to (i + 2) * M-th row" are the same.
So, you can solve this problem following way:

 Let "number of connected white parts between small calendar between 1st row to M-th row" be A
 Let "number of connected white parts between small calendar between 1st row to M * 2-th row" be B
 The answer is (B - A) * (N / M) + (2 * A - B).
 

The complexity is O(M) + O(M) = O(M).

D — Driving on a Tree

You can use the Tree-DP method in this problem.
This is a typical problem which use "Every-Direction Tree DP Algorithm" (It says "全方位木DP" in Japanese and translated directly, actually I don't know English word of the algorithm). The similar problem is 790B.
Let's consider the rooted tree which the root is node 1.

Let dp[i] be the expected value of number of moves which only go down (= to children of the node) and starts on node i
=== This value can find with Tree-DP algorithm in O(N).
Let dp2[i] be the expected value which starts on node i and go to the parent of the node first.
=== This value can find with Tree-DP algorithm (From the root of the tree to leaves) in O(N).

• Let the parent of node i be j.
• Let the degree of node i be p.
• 

The answer of node i is average of {dp[i], dp[i], ..., dp[i], dp2[i]}. dp[i] comes p - 1 times. The complexity is O(N) + O(N) = O(N).


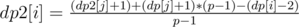
Thank you for looking this page.
I hope that you can use the commentary to solve the problem of s8pc or review the contest.

Please wait for a while for editorial between problem E to H.