I'm trying to solve 720B — Cactusophobia from Russian Code Cup 2016 Final. I read the editorial and understood the flow solution for this problem. So I find some implementation for this problem. I read dreamoon_love_AA's solution (20732895), which used Dinic flow finding algorithm and run in 373ms. But, since Dinic algorithm run in O(n2m), and the graph can have up to 30000 vertices and edges, how could this run in time? Can someone enlighten me about this? Thanks in advance.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 155 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/22/2025 20:10:22 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Sum of capacity of all edges is O(n). You can imagine an edge with capacity x as x edges with capacity 1. It'll be a unit graph, hence Dinic's algorithm will run in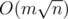 .
.
Thanks for the clear explanation.
Dinic is min(fE, V^2E), and f <= V, so it is O(VE). (As above comment mentioned, tighter bounds are possible)