coderbond007's blog

Number of path pairs from node u to any vertex having distance <= K
By coderbond007, 8 years ago, In English

How can we calculate number of node — disjoint paths pair between u and other vertex say v (such that distance of v from source vertex is K).Vertex v is not known to us. I thought of implementing BFS for every node until maximum distance from source node is <= K. But I am not getting idea for implementation. Anybody please help me? Given the number of vertices in graph can be up to than 10^5 and edges can be 6 * 10^5. In every test case, value of K will be at max 10 % of number of edges.

A path is sequence of vertices: s, v_1, .., v_m, t. Two paths s, v_1, .., v_m, t and s, u_1, ..., u_k, t are called node-disjoint if v_i != u_j for any valid i and j.

We are given a example graph shown as following. Adjacency List representation of given Directed Graph

1 - 2, 5
2 - 3, 4, 6
3 - 4
4 - 8
5 - 7
6 - 11
7 - 11
8 - 9, 10
9 - 10
10 - 11

Value of K is 6(including source node and end node). 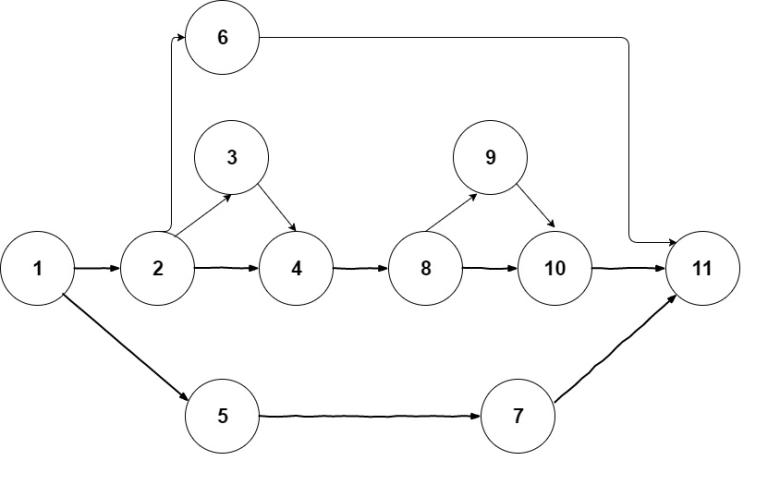Graph

Total node — disjoint path pairs possible are 3(between 1 and 11) + 1(between 2 and 4) + 1(between 8 and 10). In case of path of 1 to 11

Path 1: 1 - 6 - 11
Path 2: 1 - 2 - 4 - 8 - 10 - 11
Path 3: 1 - 5 - 7 - 11

Total combinations = Comb(3, 2) = 3

Anybody please help me out with implementation using BFS or DFS of above question. Can this question be solved using DP + DFS or DP + BFS?

UPD : In every test case, value of K will be at max 10 % of number of edges.

  • Vote: I like it
  • +4
  • Vote: I do not like it

»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

What do you mean through total combinations = comb(3, 2)? Also, is node u give to us? I see that you've counted paths that do not have either starting or ending points the same. Is the answer for that example 5?(like the sum). Ans one more thing: are you looking for the MAXIMUM number of such paths? (after trying to understand, I've assumed that, but you should still mention it in the post) Also, path 2-3-4 is not node-disjoint from path 1-2-4-8-10-11

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    No nodes are given to us. I have taken u to make the example understand-able. We have to calculate all values by itself. I am grouping paths. As we know node — disjoint paths should have initial vertex and final vertex same. So paths are 

    For all paths between 1 - 11
Path 1: 1 - 6 - 11
Path 2: 1 - 2 - 4 - 8 - 10 - 11
Path 3: 1 - 5 - 7 - 11
there combinations taking 2 at a time gives us 3 from formula (n * (n - 1) / 2).

For all paths between 2 - 4
Path 1: 2 - 3 - 4
Path 2: 2 - 4
there combinations taking 2 at a time gives us 1 from formula (n * (n - 1) / 2).

For all paths between 8 - 10
Path 1: 8 - 9 - 10
Path 2: 8 - 10
there combinations taking 2 at a time gives us 1 from formula (n * (n - 1) / 2).

All these add up to 5.

Here n is number of paths between any two nodes.

    And yes I am looking for maximum number of such paths. If you still have any doubt, feel free to ask :)

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Is the given graph acyclic? If not, then, at least theoretical, the answer could be infinity. (or you should define a path as a sequence of nodes so that you don't pass through the same node more than once). Also, do you have any restriction for K? Aaand are you sure the problem is solvable (i.e. have you got it from a reliable source)? For me, the current form, doesn't seem to have an easy polynomial solution, let alone one that could work in linear time)

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Graph can be acyclic. If graph is not acyclic than why is answer infinity? Because we are given one more constraint K. The maximum length between two nodes should not exceed K.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          Value of K will be less than N. And I am sure problem is solvable.

          → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Yeah, actually I was wrong here. Sorry. I was thinking about ignoring the K limitation to see whether I can solve it when K is large enough not to care about the length

          → Reply
          • »
            »
            »
            »
            »
            »
            8 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Can you please help me with implmentation? I was thinking to use BFS but not getting any idea of how to implement it?

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              8 years ago, # ^ |
              ← Rev. 2   Vote: I like it 0 Vote: I do not like it

              I'd help you if I could. I have no idea how to solve the problem. It seems NP to me (even though I don't have a proof yet). I don't know how BFS could be of any use in this case. It finds the shortest paths (let alone that it does this just after you fixed a starting node which already destroys your complexity) and you may have to count paths that are a little longer. Also, it's not even enough for fixed ends to compute how may paths are there between them and then take any two of them because you don't have the guarantee that any two of them are matchable

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                8 years ago, # ^ |
                  Vote: I like it 0 Vote: I do not like it

                Thanks for your reply. Can you give me idea of implementation for above graph?

                → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          You meant that it can have cycles, didn't you? Are you sure there is no other constraint? Are we asked to compute the answer modulo something? Because, if not, the answer can be really huge. Just consider N 1000 and you have edge from every i to every j. The number of pairs of path with fixed u, v is about (N-2)!*(N-2)^2 or something like that. Just printing it would take too long. And, also, could you answer the other question? That is: does that path need to contain each node at most one or not?

          → Reply
          • »
            »
            »
            »
            »
            »
            8 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Sorry for not mentioning this, if there are 400 edges for example, than value of K will be at max 40.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              8 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              And that 40 comes from where? Do you mean K<=N/10 or K<=2sqrt(N) or what? In my case, with N equal to 750 and M equal to 561750 (I took a smaller N so that M can fit in the limit), what would be the restriction of K? If K is greater than 3-4, then the answer will be huge too (not that big that you can't print it, but that big that it can't fit in long long)

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                8 years ago, # ^ |
                ← Rev. 2   Vote: I like it 0 Vote: I do not like it

                Exact number of nodes don't exceed 25000 and number of edges don't exceed 150000(approx.). And value of K is such that answer can be fit into long long.

                → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  8 years ago, # ^ |
                    Vote: I like it 0 Vote: I do not like it

                  Sorry to disappoint you, but no serious problem have this kind of constraints. Those cases that I've mentioned were just to somehow make sure that the problem doesn't specify anything else. I've tried to solve it for about 30 minutes and I couldn't find anything. But I strongly believe it's unsolvable. At least you could give a link to it...I, for one, give up

                  → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  8 years ago, # ^ |
                    Vote: I like it 0 Vote: I do not like it

                  Actually this is a part of implementation of project problem. So I cannot disclose the problem. I was trying for this part since last week and couldn't achieve solution. My solution is overestimating number of counts. That's why I posted here for help. Hope you understand.

                  → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  8 years ago, # ^ |
                    Vote: I like it 0 Vote: I do not like it

                  coderbond007 I do understand(sorry for writing here, CF didn't allow me to answer to your last comment), the only problem is that you said you're sure the problem is solvable, which you actually have no reasons to support. I honestly think the problem cannot be solved for restrictions that big. For N~16-20 some dynamic programming on configuration would work in decent time, but the initial problem that you've asked help for...well, I really believe that not even tourist could help you with that

                  → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  8 years ago, # ^ |
                  ← Rev. 2   Vote: I like it 0 Vote: I do not like it

                  Thanks for your reply. Can you give me idea of implementation for above graph? If suppose time limit is 20-30 sec, than can you implement DFS or BFS + DP?

                  → Reply