SuprDewd's blog

KTH Challenge 2017
By SuprDewd, 8 years ago, In English

KTH Challenge is an annual individual competition hosted by the KTH Royal Institute of Technology in Stockholm, Sweden. The 2017 edition starts tomorrow at 8:00 GMT, and will be 4 hours long. You can follow the local contest here, or compete at the online mirror.

For problems from previous years, see the contest website.

  • Vote: I like it
  • +63
  • Vote: I do not like it

Comments Comments (20)
| Write comment?
»
8 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Problem setters are:

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +4 Vote: I do not like it

SuprDewd Can you please, tell me something about the quality of education at KTH and the admission process for an international student. Do they get scholarships? Also, how is the faculty for Computer Science department at post-graduation level?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    I have similar question as above.I'm interested in undergraduate studies in mathematics.Are there any programs on English and what about scholarships for international students?I heard many nice things about KTH :)

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +14 Vote: I do not like it

    Neither me or SuprDewd are, or have ever been, students at KTH so we can not really answer your question, sorry.

    → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +3 Vote: I do not like it

    I am a PhD student at KTH and I can tell you that we have a nice group in algorithms and complexity, with faculty members such as Johan Håstad or Per Austrin.

    There are masters programs in English, and I think that tuition is free for students from the EU but there are fees otherwise. This page should know more than I do.

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Contest is over, so let's discuss the problems, what is the solution for EvenOdd and Global Warning? I solved Global Warning, with dynamic programming, but it's certainly not the intended solution I had to made a lot of optimizations and it passed with 1.93s.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    For Global Warming, the simplest way is probably to separate the connected components and then do the bitmask DP in O(n2n).

    For EvenOdd, given a start value x and the smallest i such that 2i ≤ x, the number of moves is i plus the number of 1s in the binary representation of 2i - x. From there you just have to figure out an efficient way (for example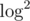 ) to compute that total number of 1s.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      My solution is O(n2 * 2n) how do you take off one of the n's of the complexity? Also how to put complexity right in the comments? Thanks in advance

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        In the bitmask loop, you always take the first non-assigned student and then try to assign it to every other non-assigned student, instead of considering every pair. Since you will always have to assign the first one at some point you don't miss possibilities.

        To insert math put dollar signs around your formula.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          How is this algorithm supposed to pass with n up to 200 ?

          → Reply
          • »
            »
            »
            »
            »
            »
            8 years ago, # ^ |
            ← Rev. 2   Vote: I like it 0 Vote: I do not like it

            There are only 250 edges, so the size of the clique will not exceed 22. (clique of 23 vertices will have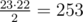 edges).

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              8 years ago, # ^ |
              ← Rev. 2   Vote: I like it 0 Vote: I do not like it

              Right, only 250 edges, but there are 200 vertices.

              For example a test case could be : 

              1 2 w1
3 4 w2
.
.
.
199 200 w100
              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                8 years ago, # ^ |
                  Vote: I like it 0 Vote: I do not like it

                You are able to process all cliques separately.

                → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +15 Vote: I do not like it

    Solution slides will be up soon on the website (http://challenge.csc.kth.se/)

    For EvenOdd, you can do the following.

    We only compute the answer for intervals [1, X] (and respond with [1, R] - [1, L - 1]).

    If X = 2Y + 1, we recurse on [1, 2Y] and add f(2Y + 1).

    If X = 2Y, we have the odd numbers 1, 3, ..., 2Y - 1 and the even numbers 2, 4, ..., 2Y. If we perform a single operation on all the even numbers we get Y + [1, Y] operations. If we perform two operations on all the odd numbers we get 2Y + [1, Y] operations. However, we should not perform operations on 1, so we remove 2 operations.

    Thus, we have [1, 2Y] = 2 * [1, Y] + 3Y - 2, so we can recurse again.

    Finally, [1, 1] = 0.

    This recursion only computes a logarithmic number of values.

    → Reply
»
8 years ago, # |
  Vote: I like it +10 Vote: I do not like it

I had the hardest time understanding the statement of Wolf and its implications. For example I'm still convinced that the only factors that matter is your number of cards and whether you own a card which is has the same suit and is bigger than one of the adversary's. In other words, I feel like it's always possible to choose and shuffle the remaining cards so that the suits are not the same when we don't want them to be. Does someone have a counterexample for that?

I did a complete search at the end so that I didn't need the hypothesis but still have WA at the moment (it might just be an implementation problem of course).

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +13 Vote: I do not like it

    I think what you're saying about always being able to shuffle is true. What we're trying to prove is that if you have a larger number of cards than your opponent, you can always perfectly match the opponent's cards to some of yours. If you examine Hall's marriage condition on the opponent's side, the only subsets that are worth checking are maximal subsets of the same suit. So the question is, can the opponent have strictly more cards of a certain suit than you have cards of the 3 different suits in total? The answer is no, because that means you would have at most 25 (L.E. actually I think this value can be 13) cards.

    As for your WA, are you checking both the case in which you win by having a greater card of the same suit and the case in which you win by making the opponent run out of cards before you?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      Oh, nice use of Hall's marriage condition, I don't know why I didn't think of that. Thanks!

      It turns out I just had an off-by-one and one of my first submissions was correct. :'(

      → Reply