21August's blog

JBOI 2015 problem Startup.
By 21August, history, 7 years ago, In English

Hi everyone. Can somebody please help me to solve this problem. Thank you very much. It is from JBOI 2015, it's called Startup.

  • Vote: I like it
  • +2
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I think it can be solved with some clever "bruteforce" approach. The first observation you should make is that for the given sequence a1, a2, ..., an we should consider sequences in form ak, ak + 1, ..., an, a1, a2, ..., ak - 1. So we should take some suffix of a and put it in front of it. Another small idea: instead of checking every prefix sum we can just check one, the minimal. So we have a correct presented sequence b1, b2, ... , bn if and only if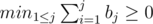 . After we conclude this we can come up with an O(N) algorithm that solves the problem by calculating the above value for prefixes and suffixes.

I hope it helps if you have more questions just ask.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thank you veru much, i will try to solve the problem after this algorithm, later and i will tell you if it worked.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Hi thanks for answering my question but i am still not able to solve it, may be you could be more specific or show me the code, but of course it would be better to explain more than to show me the code. Thank you very much.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Here is the code for the solution, it got 100 points thanks to mraron. Here is the code. Explenation: What it does is basically calculate two arrays of length n, L and R. L[i] means the smallest prefix sum of the original array till index i (you can see the recurrence in the code). R[i] means the smallest prefix sum of suffix i..n-1 (as you can see it in the code)

From then we shall see that the ith rotation meets the conditions if and only if R[i]>=0 (because i..n-1 suffix will be the new start of the array) and sum of the elements from i to n-1 plus L[i-1] is non negative because otherwise we would have some negative prefix in the middle. If you draw it, it becomes more clearer.

→ Reply