F.a.F's blog

Need help with this problem related to DP Bitmasking
By F.a.F, history, 7 years ago, In English

The problem statement is "Given a board of N(1<=N=3) rows and M(1<=M<=50) columns, place the minimum number of knights such that every cell either contains a knight or is attacked by at least one knights." 1<=T<=150 test cases

Link :- https://www.codechef.com/problems/KNICOV

I am having a hard time figuring out the states of the DP and transitions between them. Can someone please explain in detail how to go about solving this?

  • Vote: I like it
  • -3
  • Vote: I do not like it

»
7 years ago, # |
← Rev. 3   Vote: I like it +10 Vote: I do not like it

This can solve by BIT-DP. (DP with bitmasks)



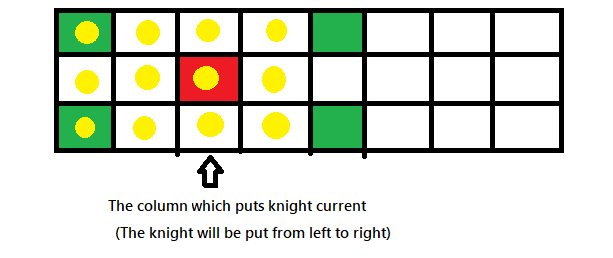
So, you should memory only 3*4=12 cells's situation in maximum.
You can solve with dp[i][j].

  • i: Current column which is putting knights.
  • j: The situation of cell (the knight was put or not) in last 2 columns, current column and next 1 column. It can be represent in bitmasks and the number of situation is 4096 (2^12) in maximum.
The complexity is O( 2M * 4 * N ).
Sorry for my poor English.
→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    somehow your time complexity seems incorrect to me.

    PS can you upload your solution?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      Maybe correct one is O(24N × M). Maybe he mistyped N and M.

      → Reply