-synx-'s blog

How to compute this GCD Sum?
By -synx-, history, 7 years ago, In English

I have been trying to solve this problem for past 2 days, but I havent come up with a formal solution.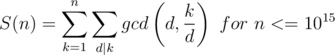

I have tried to change the order of sums and grouping by gcd but couldnt get any further than getting a bound on distinct values of gcd .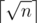
Can someone please help?
Source: PE 530

  • Vote: I like it
  • +4
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +2 Vote: I do not like it

Some hints (actually, I didn't solve problem but I'm sure this things will help for solving):

Lemma. Let d be divisor of n and GCD(n, x) = d (here x is some number). Then x = d * k for some positive integer k. Then .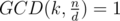

Theorem. Let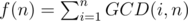 . Then 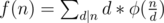. Here φ(n) is Euler function.

Bonus :) You can calculate φ(i)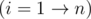 in O(nlogn) with Euler sieve.

Euler sieve code
→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    I appreciate your reply, but I already know everything you mentioned and have tried on those terms.

    And whats with the downvoting? Did I do something wrong to ask a doubt or is it glaringly easy that I have asked?

    → Reply
»
7 years ago, # |
  Vote: I like it +13 Vote: I do not like it

here is how I solved it :

let x = gcd(d,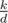) ... this means the x|d and x| 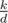which means that x2|k that means that you can compute the answer as the contribution of every x where x^2 <= 10^15

for any x with x2 ≤ 1015 notice that for any k with x2|k ... let d be any divisor such that x|d and x|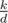 then x will be counted 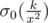times where σ0(n) is the number of divisor of n ,but there is a catch .. what if there is a y = q * x with y2|k

the way around it is to subtract y's contribution leading to a formula :

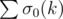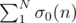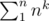but now you ask how to compute ,well there is a way to compute in O() actually it works for any power of the divisors in the same time which is O(* (time to compute )) ,I explained it briefly on the case of σ1 here ,the famous mathematician Terence Tao explained it here and you can test your understanding of it on this problem

so the answer is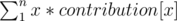 where 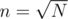and N = 1015

the time to compute all σ0 is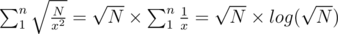

the time to compute the contribution after previous step is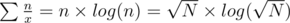 then the total time is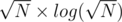

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Thanks you very much for your detailed explanation, I get the idea. And  + 1 for reference to extra problems :)

    → Reply