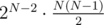Given a positive integer N, calculate the sum of inversions in every bitmask of length N.
For example, if N = 2, our masks are 00 (0 inversions), 01 (0 inversions), 10 (1 inversion), and 11 (0 inversions). We output 1.
For example, if N = 3, our masks are 000 (0 inversions), 001 (0 inversions), 010 (1 inversion), 011 (0 inversions), 100 (2 inversions), 101 (1 inversion), 110 (2 inversions), and 111 (0 inversions). We output 0+0+1+0+2+1+2+0 = 6.
How can I do this efficiently?
Please help, and thanks in advance!











You can solve it with brute force. There are 2N ways to express N bits. And you can calculate the number of inversions of N bits binary integer in O(N2). Just count the number of pair that a[i] = 1 and a[j] = 0 (i < j). So the complexity is O(2NN2).
The answer will be (average inversions) * (The number of ways).
For each pair (i, j) (i < j), if a[i] = 1 and a[j] = 0, there is an inversion in pair (i, j). So the probability is 0.52 = 0.25. There are N(N - 1) / 2 pairs, so the average value is N(N - 1) / 8.
So the answer is 2N*N(N - 1) / 8.
For each pair of indexes i < j let's calculate how many masks of length N have an inversion in this pair. It's quite easy: maski should be 1, maskj should be 0 and every other bit (there are N - 2 such bits) can be either 0 or 1. So there are 2N - 2 such masks (with an inversion on positions i, j). So each pair i < j increases the answer by 2N - 2. There are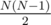 such pairs, so the total answer is
such pairs, so the total answer is