I tried to solve CEOI 2017 Day1 problem — Mousetrap today during the csacademy mirror.
My idea is a bit different than what model solution does, but in the same time complexity O(nlogn).
I'll describe it briefly. First, let's assume we can freeze the mouse for a while and prepare the way for her. Let's calculate answer for this case and call it pathOnly. This is computed by the simple formula.
Now let's unfreeze the mouse. We will do binary search on answer — how many additional operations do we need now. Let's precalculate cost[] for each vertex x, meaning: how many additional operations if mouse gets to vertex x and stays there forever. Forever means in this case: until we prepare the rest of the graph for her.
Cost is computed by a simple recursive formula : cost[onPath] = 0 and cost[x] = cost[parent[x]] + degree(x) — 1 otherwise.
Now let's move to the last step of the solution. Assume we are at some step of binsearch checking if the result can be not greater than k now. If a vertex has cost bigger than k, we should never let the mouse reach it. Otherwise, the mouse can safely get to that vertex. We compute dp[x] now -> how many operations do we need to succeed to be done before the mouse enters vertex x, dp[x] can be either 0 or 1. When a vertex is forbidden or sum of dps from its sons is greater than 1, dp[x] equals 1. Otherwise, it is 0. In the end, if dp[root] > 0, the answer for our current k does not exist and does exist otherwise.
The problem is that this solution doesn't work in at least two ways. I believe the implementation is O(nlogn) and should fit in the time limit, but it fails a lot. It gets WA twice, too. I would be very grateful if someone expressed his opinion about it.
Thanks in advance. PS. How to link the submission on csacademy?










I think one of the problem is that although pathOnly is indeed the lower bound for the answer, sometimes not all edges connected to the path from root to goal are needed to be blocked.
Like sometimes it is better for the mouse to rush to a certain node because it can gain many profit in that certain node, so for the player, she doesn't need to block any edge before that node. So pathOnly had count some extra edges.
I see what you mean. Thanks! That's probably the case. The TLE mystery is stll alive though
Hmm, I've implemented the improvement. Still, the code fails on the same testset. I don't think this was the case :/
Improved version: here
Hmm idk if this is the case, consider the path from the root to the goal, assume u is in the path, if we have to block an edge at node u, the addition(suffres) value actually get increased by now for every node v where pos[u] < pos[v] (pos is the position in the path). Which means the cost is different depend on the checking value k.
Yes, that was intented. If a mouse rushes directly to vertex x, we still have to block her those edges, because after clearing the way they will still be availbable.
I mean consider this case,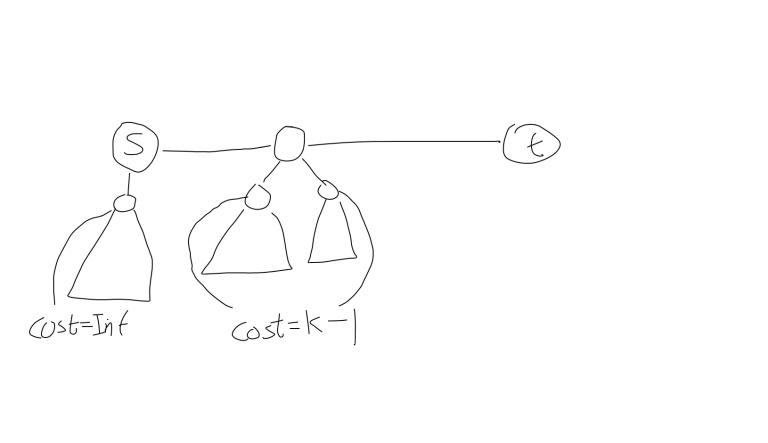
If you are in check(k), you should also consider the cost = k — 1 ones(sorry for the poor drawing...). As you have used one move before moving to the other vertex.
I've done stressteting and discovered the same testcase. Thanks! :D
Anyway, I don't care about the WA, it happens. The strangest thing is that it's O(n log n) with a relatively low constant, and it gets TLE while some solutions are O(n log n) with a relatively high constant..
"I don't care about the WA, it happens"
-Kacper Walentynowicz
I like you too.
BTW I don't know about mirror but on competition I was doing last part(of choosing which nodes to block on path) in O(n^2) and it fricking passed :D :D (But I did have everything figured out and I would have solved anyways)
Yeah, this one was pretty hard, took me a few hours and a few bad ideas to solve. I'm doing something probably similar to you, but the binsearch needs to be very careful.
For each edge x->y leading away from the path m-t, I compute cost[y]: the number of actions that need to be taken within the subtree of x (the tree is rooted at m) if the mouse uses that edge. Now, to check if the answer is ≤ c, the binsearch computes for each v on the path from m to t the number of moves available to block the mouse's path before it moves from v and the number of moves M[v] that have to be spent (strictly) above v; these 2 sequences determine if it's possible. The key difference from your algorithm is probably that I decide that the mouse can use some edge v->y only when I know the number M[v]. If cost[y] > c - M[v], then it has to be blocked before the mouse gets there. If the next vertex is w, then M[w] = M[v] + the number of such blocked edges — when they're blocked, the mouse will go to w, since there's no way it can do better than c otherwise.
Ad TLE: My code takes about the same time as you (800ms) on 2m cins and push_backs, then ~300ms on one DFS, then 0ms (+- standard timer error) on sorting a vector of size 1m and the binsearch. What kind of sorcery...
Ad tle: I'm totally out of ideas. The only n log n part is binsearch, it should run very fast, but somehow įt doesn't. Erasing one for inside it gives one sec time difference. Maybe some c++ expert will look at it and say "oh you can't into using c++ properly"
I found out that changing
dp[parent[x]] += dp[x]todp[par2[i]] += dp[x]wherepar2[i]=parent[POST[i]]is precomputed improves the time to < 2100ms. I'm guessing the former can't be optimised well and the latter can.