The recurrence
f(i, i) = 0
f(i, j) = g(f(i, j - 1), f(i + 1, j)) + cost(i, j)
for any function g and cost (minimum and (i + j), respectively, for example) generates a family of graphs that (informally) look like a complete binary tree that cuts into itself.
Has this family of graphs been named? Does it have properties that could be useful in competitive programming?
Notable things:
The graphs have no Euler path nor circuit for depths larger than 2.
Maximal independent set is taking the last depth, third last depth, etc.
Seems like Hamiltonian paths don't exist for larger depths.
Hamiltonian circuits definitely don't exist, since there are vertices with degree 1.
Odd cycles don't seem to exist, which means the graphs are bipartite
Screenshot courtesy of VisuAlgo 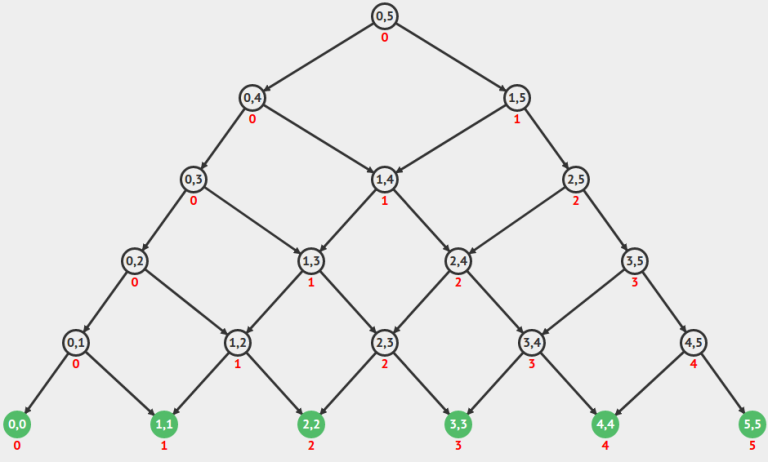











"Pascal triangle thingy"
Corners of square grid: