wish_me's blog

Non-decreasing subsequence of size k with minimum sum
By wish_me, 7 years ago, In English

Given a sequence of n integers, you have to find out the non-decreasing subsequence of length k with minimum sum. If no sequence exists output -1.

Examples:

Input : [58 12 11 12 82 30 20 77 16 86], k = 3 Output : 39 {11 + 12 + 16}

Input : [58 12 11 12 82 30 20 77 16 86], k = 4 Output : 120 {11 + 12 + 20 + 77}

Input : [58 12 11 12 82 30 20 77 16 86], k = 5 Output : 206

  • Vote: I like it
  • -10
  • Vote: I do not like it

Comments Comments (11)
| Write comment?
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If you are looking for a solution than here

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

what's your expected time complexity?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    In my article which I wrote, the time complexity is O(n^2*k).

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Looks like O(N^2*K) to me.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        let dp[i][j] represents that we pick i-th number, we get a non-decreasing subsequence which has a size of j, the minimum sum of it.

        so naively u can solve it in O(n2 × k)

        with bit/range tree you can optimize to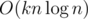 i think?

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          I know, I was talking about the code from the blog this guy linked. Still, your comment may be helpful for the one asking the question.

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
            ← Rev. 2   Vote: I like it 0 Vote: I do not like it

            gg i just realized that i replied to the wrong person..sry

            → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +8 Vote: I do not like it

          Can you explain first method please?

          → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        Can you explain please?

        → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    I am expecting knlogn? Is it possible?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 4   Vote: I like it 0 Vote: I do not like it

      Let's go with i through our array and store k Fenwick trees to find minimum of prefix. Get(bit[j], x) returns minimum sum of non-decreasing subsequence of length j which last element is not greater than x.

      Now we want to continue some sequences with our a[i]. For a certain sequence length j we can make sequence of length (j + 1) with minimum sum S = Get(bit[j], a[i]) + a[i], then minimise(bit[j + 1], a[i], S). Correct me if i'm wrong.

      → Reply