А. Ярмарка оружия [реализация, математика]

Необходимо последовательно сравнить силы наборов, если текущая сила строго больше максимальной предыдущей, то обновляем максимальную и индекс лучшего набора. Вычислить силу набора можно было в нецелых числах как (сумма s_i, j / w_i), или сохранить числитель и знаменатель дроби (sum_smax и w_max) и сравнивая с текущим набором домножить обе части на (w_max·w_i). Не стоит забывать, что суммирование 10⁵ чисел до 10⁹ приведёт к переполнению типа integer.

Асимптотика: O(n·max(w_i))

Код в нецелых числах

Код в целых числах

B. Имённо-фамильный никнейм [перебор, строки]

Любое решение сводится к тому, чтобы максимизировать подстроку в n (ведь чем больше символов мы возьмём из n, тем меньше потребуется из f).

Обозначим длину такой подстроки за k.

1) Наивное решение может проверять все подстроки строки n для поиска максимального k, после чего искать недостающий конец строки в f. Это будет работать за O(q·|n|² + q·|f|) в теории, однако лишь в худшем частном случае, когда множество раз наблюдается значительное совпадение подстроки с первой часть строки s_i (пример: n = " ", f = " ", и все s_i = " ").

Код

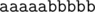2) Подсчитать все возможные подстроки для n за |n|², сложить в set[string] или бор, или подсчитать хеши (это будет работать аналогично set[string]). Теперь для каждого s_i можно последовательно искать k, после чего можно пройтись последовательно по f, узнав, есть ли там оставшиеся |s_i| - k символов. При использовании set[string] или хешей можно также искать k бинарным поиском, укорачивая или удлиняя текущую строку до длины M на каждой итерации и ища ей соответствие в подстроках n.

Асимптотики такого решения:

• Для хешей или set:
  • если искать k последовательно: O(q·k·log₂(|n|²) + q·|f|)
  • бинарным поиском: O(q·log₂(k)·log₂(|n|²) + q·|f|)
• Для бора: O(q·k + q·|f|)

Код с set[string], последовательная проверка k

Код с set[string], бинарный поиск по k

Код с бором

3) Развернём n, f, и s_i задом наперёд. Тогда нам нужно максимизировать не подстроку, а подпоследовательность в f, в этом единственное отличие от предыдущего варианта. Искать k для подпоследовательности можно только последовательно, после чего нам нужно найти в n подстроку длины |n| - k, для чего опять же следует предподсчитать все возможные подстроки для n за |n|² и сложить их в какую-нибудь структуру.

Асимптотика решения:

• Для хешей или set[string]: O(q·k + q·log₂(|n|²))
• Для бора: O(q·k + q·|n|)

C. Два великана [игры, математика]

Очевидно, что размер кучи от 1 до x является выигрышным для Тора, т.к. он может сломать её одним ударом.

А теперь давайте подумаем насчет n = x + 1. Если Тор сломает 1 кирпич, останется x кирпичей, и Арен победит, если Тор сломает x кирпичей, Арену останется 1 кирпич и он тоже выиграет.

Значит, куча размера x + 1 всегда является проигрышной для Тора. А это в свою очередь значит, что все кучи от x + 2 до 2x + 1 являются выигрышными — Тор может всегда сломать столько кирпичей, что Арену достанется куча размера x + 1 и тот проиграет.

Подобным образом рассуждаем дальше, применяя важное правило теории игр — если из состояния текущего игрока нет способа привести состояние в проигрышное (чтобы в нём оказался другой игрок, а текущий выиграл), значит для текущего игрока состояние проигрышное, и при оптимальной игре обеих сторон он всегда будет в проигрышном состоянии, а другой игрок наоборот, в выигрышном.

И получаем, что проигрышными для Тора являются только кучи кратные x + 1 (x + 1, 2x + 2, 3x + 3, ..). Тогда ответ на отрезке [1;n] можно найти как 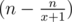, обозначим это функцией f(n), тогда ответ на отрезке [L;R] равняется f(R) - f(L - 1).

Асимптотика: O(q)

Код

D. Кровожадная функция [математика]

Итак, f(x) = a^x·(b + x)^x·c. Нам даны три значения этой функции, давайте распишем их в полном виде:

f(0) = a⁰·(b + 0)⁰·c = 1·1·c = c

f(1) = a¹·(b + 1)¹·c = a·(b + 1)·c

f(2) = a²·(b + 2)²·c

Как видим, c = f(0). Значит можно упростить два других выражения:

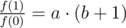
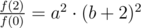
Что мешает избавиться от квадрата во втором выражении?

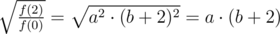
Теперь можно найти a:

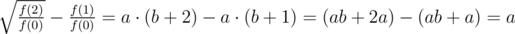
И b:

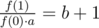
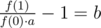
Асимптотика: O(1)

Код

E. Интересная структура [математика, реализация]

Так как x не превосходит 100, можно было хранить массив cnt[100] и прибавлять или отнимать количество чисел в явном виде. При запросе третьего типа необходимо пройтись по всем числам от 1 до 100 и умножить текущий остаток на x^cnt[x] по модулю m.

Однако cnt[x] может быть весьма большим, и каждый раз умножать в явном виде слишком долго. Здесь есть два пути оптимизации:

1) будем хранить стек значений val[x], где val[x][cnt[x]] равняется x^cnt[x] % m. Сделаем val[x][0] = 1 изначально для всех x от 1 о 100, тогда при добавлении нового числа x в структуру будем помешать в конец стека новое значение на основе предыдущего: val[x].push_back( (val[x][ cnt[x] ] * x) % m ); А при запросе второго типа нам просто нужно убрать последнее значение из стека: val[x].pop_back().

Также вместо стека можно было использовать массив val[100][100000] (т.к. очевидно что любое число будет повторяться не более q раз, т.е. не более 10⁵ раз), но это более затратно по памяти.

Асимптотика: O(q + 100·cnt_t3)

Код со стеком

Код с массивом

2) воспользуемся быстрым возведением в степень (более подробно здесь, основная идея в том, что xⁿ = x^n / 2·x^n / 2)

Асимптотика: O(q + 100·cnt_t3·log2(cnt[x]).

Код

+) можно не пересчитывать ответ каждый раз на запрос третьего типа, а лишь в тех случаях когда мы вносили изменение (т.е. это оптимизация на случай множественный запросов третьего типа).

+) можно хранить числа не в явном виде, а факторизовать их (раскладывать на простые) и считать ответ по степеням простых чисел от 1 до 100 (их 25 штук). Авторское решение использовало именно факторизацию + быстрое возведение в степень: O(q·log2(x) + 25·cnt_t3·log2(cnt[x])).

Код авторского решения

F. Статически полный граф [тролль]

Если Вы хоть немного знаете о том, что такое графы, Вы сможете решить эту задачу.

Главное — внимательно прочитать все условия и подумать что они означают.