Блог пользователя 300iq

Рандомизированный поиск пересечения полуплоскостей
Автор 300iq, история, 7 лет назад, По-русски

На контесте в ЛКШ зашел следующий алгоритм:

Шафлим полуплоскости, перебираем пару, находим точку пересечения, бежим по всем полуплоскостям, когда встречаем полуплоскость в которой эта точка не лежит -> break; Дальше строим выпуклую оболочку всех точек, которые лежат во всех полуплоскостях.

Полуплоскостей было <= 2000.

Слабые тесты или матожидание времени работы быстрее куба?

  • Проголосовать: нравится
  • +54
  • Проголосовать: не нравится

»
7 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Ну например, все 2000 прямых проходят через 0, звучит как контртест.

→ Ответить
»
7 лет назад, # |
← Rev. 2   Проголосовать: нравится +93 Проголосовать: не нравится

Пусть всего у нас n полуплоскостей. Сначала поймем, что если какую-то точку не содержат k полуплоскостей, а n - k содержат, то алгоритм потратит на нее в среднем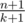 времени(ну или ровно n при k = 0, это мелочи).

Возьмем одну из данных прямых и пересечем со всеми остальными полуплоскостями. Получим набор лучей, одни идут "вправо", другие "влево", возьмем например те что "вправо". На самую правую точку из начал таких лучей мы потратим не больше n, на следующую не больше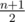 , потому что она точно не содержится в полуплоскости(-тях), которые нам дали самую правую точку, на следующую аналогично не больше 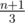, и так далее; всего точек не больше n, т.е. суммарно на все такие точки потратим не больше .

Осталось не забыть про все лучи, идущие "влево" и просуммировать наши затраты по всем прямым полуплоскостей; суммарно . Кажется, что на правильном многоугольнике это как раз и достигается.

→ Ответить
  • »
    »
    7 лет назад, # ^ |
    ← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

    Возможно, во втором абзаце правильней писать "в среднем не более" или это подразумевается.

    "Кажется, что на правильном многоугольнике это как раз и достигается." — наверно имеется в виду такой, у кот-го кол-во вершин равно n.

    Получается нужно просто брать крайние точки среди "левых" и "правых" и если они составляют не пустой отрезок, то он явл-ся ребром искомого многоуг-ка, после этого переходить на прямые, кот-е дают эти точки и получим решение за O(n^2) в худшем случае?

    → Ответить
»
7 лет назад, # |
  Проголосовать: нравится -15 Проголосовать: не нравится

подскажите пожалуйста как шафлить полуплоскости

→ Ответить
  • »
    »
    7 лет назад, # ^ |
    ← Rev. 2   Проголосовать: нравится +34 Проголосовать: не нравится 
    vector<Halfplane> halfplanes;
random_shuffle(halfplanes.begin(), halfplanes.end());
    → Ответить
    • »
      »
      »
      7 лет назад, # ^ |
      ← Rev. 3   Проголосовать: нравится +31 Проголосовать: не нравится

      Я предпочитаю

      mt19937 rnd(228);

...

vector<Halfplane> halfplanes;
shuffle(halfplanes.begin(), halfplanes.end(), rnd);
      → Ответить
      • »
        »
        »
        »
        7 лет назад, # ^ |
          Проголосовать: нравится -49 Проголосовать: не нравится

        Я предпочитаю

        int cur = 2, P = 300, Q = "iq", T = "300iq";

        int rnd() { cur = (cur * Q + T) % P; return cur; }

        ...

        vector halfplanes; shuffle(halfplanes.begin(), halfplanes.end(), rnd);

        → Ответить
        • »
          »
          »
          »
          »
          7 лет назад, # ^ |
            Проголосовать: нравится +18 Проголосовать: не нравится

          Мне кажется peltorator предпочитает CE.
          Нужны одинарные кавычки.

          → Ответить
          • »
            »
            »
            »
            »
            »
            7 лет назад, # ^ |
              Проголосовать: нравится -38 Проголосовать: не нравится

            Мне кажется, up-and-down предпочитает выкладывать в сеть приватную информацию людей, а я написал псевдокод

            → Ответить
      • »
        »
        »
        »
        7 лет назад, # ^ |
          Проголосовать: нравится 0 Проголосовать: не нравится

        спасибо, думаю это верно

        → Ответить