HolkinPV's blog

Codeforces Round #141 (Div. 2)
By HolkinPV, 12 years ago, translation, In English

Welcome, friends)

We are glad to introduce you regular Codeforces round #141 for Div.2 participants. But traditionally the others can take part out of the competition.

Problems are prepared by command of authors: Pavel Kholkin (HolkinPV), Ivan Fefer (Fefer_Ivan), Igor Kudryashov (Igor_Kudryashov) and Gerald Agapov (Gerald). Traditionally thanks to Michael Mirzayanov (MikeMirzayanov) for perfect Codeforces system and Mary Belova (Delinur) for translating problems.

Score distribution is standard.

We wish you good luck, successful hacks and high rating!

UPD: the contest is over, hope you enjoy it) Congratulations to winners:

1) AntiFate

2) alicechennan

3) honeyofsistercha

4) Fride

5) bla_bla_bla

UPD2: the editorial was already published, you can find it here

  • Vote: I like it
  • +77
  • Vote: I do not like it

Comments Comments (35)
| Write comment?
»
12 years ago, # |
  Vote: I like it +8 Vote: I do not like it

When you decide which type of score distribution to choose, what do you base your decision on?

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it -11 Vote: I do not like it

    already mentioned. "Score distribution is standard." that means in ascending order.

    → Reply
    • »
      »
      »
      12 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      I think his Question ,why he choose standard and doesn't choose dynamic ? what's the decision based on ?

      → Reply
      • »
        »
        »
        »
        12 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        sorry for that. I am still learning english....

        → Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    I am guessing it is based on how confident the authors are of the difficulty level of the problems. If they are very confident then standard score distribution otherwise dynamic.

    → Reply
»
12 years ago, # |
  Vote: I like it +10 Vote: I do not like it

First off, great problem set. Seems like many people managed to solve E (grats), I would like to know the trick!

I reduced the problem to finding a sequence of nodes (with repetition allowed) that by using XOR, and including the initial state, would yield only ones. If i'm on the right track you probably understand what I mean, if im not please ignore. Anyway, can somebody hint for the solution?

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +2 Vote: I do not like it

    Not a sequence, but a set (doesn't make sense to paint a city twice, and also the order doesn't matter). Color blue the cities you're going to paint, and the other ones red. Now an asphalted edge means the colors of the cities it connects must be equal, non-asphalted — they must be distinct. Then see 2-coloring of graphs.

    → Reply
»
12 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Lame...I totally ignored the alert that an all white fractal and an all black fractal are valid fractals.

→ Reply
»
12 years ago, # |
  Vote: I like it +15 Vote: I do not like it

Regarding the rule: "_He divides the sheet into four identical squares. A part of them is painted black according to the fractal pattern._", I think the example for C is not illustrative enough...

I thought "a part of them" means one of the 4 parts... And it takes me quite a while to understand why a "2x2 black" square is a valid fractal pattern.

→ Reply
»
12 years ago, # |
  Vote: I like it +1 Vote: I do not like it

I am bit confused about sample given for Problem E(probably I am misreading problem).

example had

4 4 1 2 1 2 4 0 4 3 1 3 2 0

if road build go to first city 2 and then to 1, it would asphalt all roads?? after it go to city 2=> 1st road would unasphalt and 2nd/4th road would asphalted after he go to city 1=> 1st road would be asphalted

hence after 2 step it should get asphalted, can someone help me where I am misinterpreting the problem

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    You are absolutely correct, 2 1 2 Is an answer, however it's not said you should print the minimal answer so 4 3 1 2 3 Is also an answer.

    → Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    When multiple solutions exist, print any.

    → Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    You are right.
    2
    2 1
    is valid answer for the first sample test.

    In this problem you can output any solution that need less than n steps.

    → Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    I'm also confused about the sample, but it says

    he asked you to make a program that determines whether you can "in some way" asphalt Berlandian roads in "at most" n days.

    you don't need to output the minimum number of days, so 4 3 1 2 3 in the sample is also a correct answer.

    → Reply
»
12 years ago, # |
  Vote: I like it +2 Vote: I do not like it

I hope editorial will be available soon.

→ Reply
»
12 years ago, # |
  Vote: I like it +6 Vote: I do not like it

My solution to task E First we notice that doing the operation (asphalting) on town X will XOR all the roads coming out of it, so it's obvious that you don't need to do the operation (asphalting) on the same town more than once. (XOR-ing a road 2 times, is the same as XOR-ing it 0 times) So as we know that, we know for every town, we either asphalted the roads coming out of it once, or we didn't at all. Now let's take a set of connected towns (you can reach each town in the set from each town in the set) , Now if we know for one town if we asphalted it, then we can find out if we asphalted for each of the towns in the set. Example : We take a random town in the set and say we didn't asphalt it, we check every town he is connected to with a road that is not asphalted, obviously the other town must be asphalted if we want the road to ever be asphalted, and we check every town he is connected to with a road that is asphalted, obviously the other town shouldn't be asphalted. This way we repeat for every new town we find and because it's connected graph, we will find out for all of them. Now if we get for a town, that it should be asphalted and at the same time not asphalted, we got impossible situation. Then we repeat the whole thing but saying we asphalted the random town we took. So if both cases return impossible, we print impossible, in other case , we stop looking at this connected graph and say we managed to do it , then we proceed and take another connected set, doing the exactly same thing. If we end up doing all the sets without problems, we print the towns we asphalted from (we memorize them). Since we said a town can be asphalted at most once, the limit, to asphalt at most n towns, doesn't really do anything (asphalting all towns will result in n asphalts).

Sorry if i didn't explain it quite well, just thought i'd share my idea with you, it worked and i got 54th place :)

→ Reply
»
12 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Nice problemset, but one question. How did you define a "fractal pattern"? naturally thinking, why a pattern with 0 or 4 blocks in black grids is vaild, with exactly 1 also works, but doesn't for exactly 3 black grids? It has just gone beyond my imagination..

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Why doesn't it work for 3 black grids?

    → Reply
    • »
      »
      »
      12 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I'm still confused... can you list out all "fractal pattern"? easy job for there will be at most 16.

      → Reply
      • »
        »
        »
        »
        12 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        There are exactly 16 fractal patterns. Every cell can be either black or white regardless on other cells.

        → Reply
        • »
          »
          »
          »
          »
          12 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Thanks. Finally I realized that "A PART OF THEM" means arbitrary instead of exactly one of them.

          → Reply
»
12 years ago, # |
  Vote: I like it +9 Vote: I do not like it

Can you update the rating please so I can sleep well ?

→ Reply
»
12 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Did anybody model the problem E with 2-SAT my solution failed in test case 43

if c == 0 then either of a or b can be taken but not both so i did this: (a or b) and (!a or !b)

if c == 1 I initially did (!a or b) and (a or !b) and (a or b)

It gave Impossible in first case

Why it did not work?

→ Reply
  • »
    »
    12 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    Intersting. I tried to solve this problem by creating a linear equations system with m equations and n variables, taking XOR (or plus %2) on everthing.

    This approuch is different from yours but I think the idea behind them are the same (you are modeling that a XOR b = NOT c like me, althogh you maybe want to remove the clause (a or b) for the case c==1, to make (!a, !b) possible).

    I also failed in test case 43, so I think it was probally for the same mistake. Does someone know why this idea could fail?

    UPD: Got AC. My code just contained bugs, not related to this ideia. It must be correct.

    → Reply
    • »
      »
      »
      12 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      You can read my comment below, I used this approach to get E passed.

      → Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think this formula is not correct: "if c == 1 I initially did (!a or b) and (a or !b) and (a or b)"

    The part (a or b) is wrong, because when (a = 0 and b = 0) it return 0, but actually in this case it should return 1.

    The correct formula should be: if c == 1 then (!a or b) and (a or !b)

    → Reply
    • »
      »
      »
      12 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank everyone. @pele yah you are right i did not handle when both of them can be 0. deleting (a or b) got AC.

      Again thanks.

      → Reply
»
12 years ago, # |
  Vote: I like it +9 Vote: I do not like it

For those who are seeking for non dfs/2SAT solutions in E:

Actually it is a system of Boolean equations with 2 variables each, the condition is to set the edge connecting i and j to be colored, with given color condition k (either 0 or 1). So we get for each edge, an equation like

and can be rewritten as

You will get m equations for n variables. Note that there is no unique solution (if it exists) since there are no two different equations with the same pair of variables with different coefficients on LHS (it's just 0 or 1 anyway). It means that if solutions exists, there is at least one slack variable, and the solution size is always less than n.

Solving the equation can be done using Gaussian Elimination in O(mn2) time. A faster approach is to utilize the property that each equation has exactly two variables. when doing elimination, the row being update always contains exactly two variables as well. Suppose we pick the equation

with i < j. Now we want to eliminate

where i < k. WLOG assume j < k. You get

Steps to consider.

(1) We saw an equation being set with (xj, xk) such that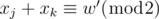

(i) if w = w', this is a redundant equation, we forget it and process next edge.

(ii) otherwise, contradiction occurs, no solution.

(2) If we haven't seen such pair (xj, xk), and there is no equation with pairs (xj, xp) with j < p, we set up this new equation (that xj relies on xk for backward substitution).

(3) If we have an equation with pairs (xj, xp) with j < p and p ≠ k, we eliminate the obtained equation with it to get a new one with pair (xp, xk) (assume p < k). Then go back to step (1).

Hence we see that step (1) to step (3) would go at most n times, so we obtain at most n - 1 equations after processing m edges, and do backward substitutions. It takes O(mn) time.

→ Reply
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone help me find the wrong in my submission?Because it's right when running on my own computer.thx.2261761

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    Make sure to fix these warnings first:

    x.cpp: In function 'int main()':
x.cpp:83:93: warning: format '%c' expects argument of type 'char*', but argument 2 has type 'int*' [-Wformat]
x.cpp:88:93: warning: format '%c' expects argument of type 'char*', but argument 2 has type 'int*' [-Wformat]
x.cpp:90:13: warning: declaration of 'x' shadows a global declaration [-Wshadow]
x.cpp:55:5: warning: shadowed declaration is here [-Wshadow]
x.cpp:91:17: warning: declaration of 'y' shadows a global declaration [-Wshadow]
x.cpp:55:8: warning: shadowed declaration is here [-Wshadow]
    → Reply
»
12 years ago, # |
  Vote: I like it +6 Vote: I do not like it

Why hasn't the editorial yet been published???

→ Reply