78A - Haiku

Count the total number of “a, e, i, o, u” in each line, and check whether they satisfy the form of “5, 7, 5”.

78B - Easter Eggs

For simplicity, we use 0, 1, 2,...,6 to denote the seven colors. The following pattern always satisties the requirement 012345634563456345634...

78C - Beaver Game

A very interesting problem!!

We use FIRST to denote the player who moves first, and SECOND to denote the other player. If n is an even number, this results in a perfectly “symmetric” situation, and SECOND always wins since he can simply “copy” what FIRST has done. As long as FIRST can succeed cutting the logs, SECOND can also make it.

When n is an odd number, it becomes a little complicated. We write m = XY, where both X and Y are divisors of m, and it also means that the original log of length m has been cut into X new logs with the same length Y. To satisfy Y ≥ k, we should have 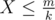. If we set X as the maximum divisor that satisfies this condition, then none of the logs of length Y can be further cut. We can prove this by contradiction. Assume that Y can be further cut, which implies that Y = pq, and q ≥ k. Thus, we can obtain a larger X' = Xp, which is impossible since we have set the maximum value to X.

Therefore, FIRST can first cut any original log so that none of the new logs can be further cut. Then, the situation is equivalent to saying that we are given n - 1 (an even number) logs while rightnow SECOND is the first one to move, and thus FIRST wins. Be careful that X cannot be 1, and thus if X = 1, FIRST still loses.

78D - Archer's Shot

A wonderful mathematical problem. We count the number of hexagons column by column. We denote the column that contains the center “A” as the first column. According to the symmetry, it is sufficient to focus on the columns to the right of “A”, inclusively. For each column, we use binary search to find the highest hexagon. Again due to the symmetry, we only need to count the hexagons above “A”.

For the hexagon with height h, we can check two points, the right upper point and the rightmost point, to see whether both of them fall inside the circle or not. If yes, this hexagon is covered by the circle; otherwise not. The left work is to compute the distance of these two points from the center, which needs some simple geometric calculation (using Pythagorean theorem) and omitted here.