A simple problem with straightforward solution. Divide the given string into 8 parts with the same length 10, and convert each of them to a decimal digit according to the provided mapping relationship.
Generate all the feasible C53 patterns, and check whether there exist any three people that are either known or unknown to each other. The mutual relationship can be represented by the connectivity of graph.
This is a horrible problem...There are a huge number of cases that should be considered. One of the cases that is likely to be ignored is shown as follows:
Suppose that m = 4, n = 100, and a = 3, b = 10. One might give 3 as the answer. However the answer should be 2, since we can first select 3, 4, 7, 8, and then select 5, 6, 9, 10.
It turns out that greedy algorithm solves this problem. Assume that we have n segment lines with the same length w, and we put them one after another, i.e., the i-th one starts from the end of the previous one. Next, we have another m segment lines with the same length 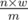 , and also put them in the same manner as mentioned above.
, and also put them in the same manner as mentioned above.
For each segment line with length w, we check whether it contains more than two segment lines with length 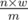 . If yes, the answer is NO; otherwise we can further calculate the “contents” in each cup by checking what are included in each of the m segment lines.
. If yes, the answer is NO; otherwise we can further calculate the “contents” in each cup by checking what are included in each of the m segment lines.
Note that if we use “float” types, we may fail obtaining sufficiently precise results, especially under some weird cases. The best choice is to replace all the division with an equivalent multiplication.
At first, I consider using DP to solve this problem. For instance, we can use dp[n] to denote the minimum number of operations to obtain the integer n. We can find out all pairs of (i, j) and coefficients k = 1, 2, 4, 8 so that n = i + k × j holds and dp[n] = dp[i] + dp[j] + 1. However, this fails since dp[i] and dp[j] are dependent under some cases. For instance n = 138, and the optimal decomposition is 138 = 2 + 8 × 17 and 17 = 1 + 8 × 2. Here dp[17] = 2 and dp[2] = 1, and thus dp[138] = 4. However the optimal answer should be 3 since after we obtain 2, the number of operations to obtain 17 is reduced to 1 instead of 2.
It turns out that this problem can be solved by using DFS with powerful branch and bound tricks. In detail, we just keep generating values by using the values that have already been calculated, and assign them to the registers that have not been consumed. When all the registers have been used or we have got the target value n, the call of DFS function should be terminated immediately to significantly reduce the comlexity.
At first we derive the recursive formula. We use f(a1, a2, ..., ak)[n] to denote the target value. Suppose that we have obtained f(a2, ..., ak)[n], and to calculate the target value, we should further delete the integers which are divisible by a1. These integers have form q × a1, but q is not divisible by any a2, a3, ..., ak, since we have chosen them in such a manner. Moreover, 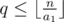 holds, and thus f(a1, a2, ..., ak)[n] = f(a2, ..., ak)[n] - f(a2, ..., ak)[n / a1], where “/” denotes the integer division.
holds, and thus f(a1, a2, ..., ak)[n] = f(a2, ..., ak)[n] - f(a2, ..., ak)[n / a1], where “/” denotes the integer division.
With the above formula, we can compute the result based on DFS. For small n, we can calculate f(a1, a2, ..., ak)[n] in previous to reduce the search complexity. Furthermore, we can sort (a1, a2, ..., ak) in a decreasing order in order to decrease “n” as fast as possible, for each call of DFS.









