Hi, Codeforces Community!
Codefest'17 — a diverse roster of high-quality programming competitions by Department of Computer Science and Engineering, IIT Varanasi is excited to present Mathmania — the mathematical puzzle contest.
The contest will take place at HackerRank (https://www.hackerrank.com/mathmania-codefest17 ). This contest will be an individual event with a duration of 3 hours, from Sep/23/2017 15:30 UTC.
It will bring a delectable collection of problems which will be an absolute delight for all the mathematics geeks. Cash prizes worth INR 50,000 will only add to the intensity.

Although mathematical insights and tricks will be crucial to cracking the challenges, programming will be your way out for the full solution. :)
Prizes -
1st (Overall) — INR 20,000
2nd (Overall) — INR 12,000
3rd (Overall) — INR 8,000
1st (India) — INR 7,000
1st (IIT Varanasi) — INR 3,000
To be eligible for the prizes you must be registered for the Mathmania event on http://codefest.tech/dashboard/events/.
Come on now, programming is a bit stale without mathematics. Accept it with enthusiasm, or accept it grudgingly — but you cannot run away from this one!










How to solve the last problem? I couldn't debug it, always getting zero determinant for some small N (N = 15).
First of all, let M(i, j) be equal to 1, if L(i, j) > 0, otherwise 0. It's clear that
Now find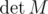 . It's almost upper-triangular matrix, so one can see that each sequence
. It's almost upper-triangular matrix, so one can see that each sequence
adds $(-1)^k$ to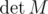 . It's easy to calculate
. It's easy to calculate
dp[parity][n]corresponding for the number of such sequences ending withnand having length with parityparity.why,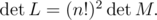
How to solve the second last problem "Alien Elimination"?
For each n let Fn be the number of permutations of {1, 2, . . . , n} with the required property; call them good. For n = 1, 2, 3 every permutation is good, so F1 = 1, F2 = 2, F3 = 6.
Take an n > 3 and consider any good permutation (a1, a2, . . . , an) of {1, 2, . . . , n}. Then n − 1 must be a divisor of the number
2(a1 + a2 + · · · + an−1)
= 2(1 + 2 + · · · + n − an )
= n(n + 1) − 2an = (n + 2)(n − 1) + (2 − 2an ).
So 2an − 2 must be divisible by n − 1, hence equal to 0 or n − 1 or 2n − 2. This means that an = 1 or an = (n + 1)/2 or an = n. Suppose that an = (n + 1)/2. Since the permutation is good, taking k = n−2 we get that n-2 has to be a divisor of
2(a1 + a2 + · · · + an−2) = 2(1 + 2 + · · · + n) − an − an−1
= n(n + 1) − (n + 1) − 2an−1 = (n + 2)(n − 2) + (3 − 2an−1).
So 2an−1 − 3 should be divisible by n − 2, hence equal to 0 or n − 2 or 2n − 4. Obviously 0 and 2n − 4 are excluded because 2an−1 − 3 is odd. The remaining possibility (2an−1 − 3 = n − 2) leads to an−1 = (n + 1)/2 = an, which also cannot hold. This eliminates (n + 1)/2 as a possible value of an. Consequently an = 1 or an = n.
If an = n then (a1, a2, . . . , an−1) is a good permutation of {1, 2, . . . , n−1}. There are Fn−1 such permutations. Attaching n to any one of them at the end creates a good permutation of {1, 2, . . . , n}.
If an = 1 then (a1−1, a2−1, . . . , an−1−1) is a permutation of {1, 2, . . . , n−1}. It is also good because the number 2(a1−1) + · · · + (ak−1) = 2(a1 + · · · + ak) − 2k is divisible by k, for any k ≤ n − 1. And again, any one of the Fn−1 good permutations (b1, b2, . . . , bn−1) of {1, 2, . . . , n−1} gives rise to a good permutation of {1, 2, . . . , n} whose last term is 1, namely (b1+1, b2+1, . . . , bn−1+1, 1).
The bijective correspondences established in both cases show that there are Fn−1 good permutations of {1, 2, . . . , n} with the last term 1 and also Fn−1 good permutations of {1, 2, . . . , n} with the last term n. Hence follows the recurrence Fn = 2Fn−1. With the base value F3 = 6 this gives the outcome formula Fn = 3 * 2n−2 for n ≥ 3.
How to solve Snuffles Trouble https://www.hackerrank.com/contests/mathmania-codefest17/challenges/snuffles-troubles the best i could think of was segmented sieve and prime factorization in O(n^1/3) for n<=10^18