wish_me's blog

Count all subsequences having product less than K
By wish_me, history, 7 years ago, In English

Given a non negative array, find the number of subsequences having product smaller than K.

k<10^2 arr.size<10^3

Examples:

Input : [1, 2, 3, 4] 

k = 10

Output :11

The subsequences are {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {1, 2, 3}, {1, 2, 4}

Input : [4, 8, 7, 2] 

k = 50

Output : 9

  • Vote: I like it
  • +6
  • Vote: I do not like it

Comments Comments (12)
| Write comment?
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I think the brute-force solution may work. Any judge to submit?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If the size is more then what to do other than brute-force?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      I don't know about the exact time complexity of brute-force solution but the solution mentioned by -Morass- is correct and works in O(n*k).

      → Reply
»
7 years ago, # |
  Vote: I like it -19 Vote: I do not like it

Here, since input size is less than or equal to 1000, we can just consider all the subsequences and find the product of each of them. For example, we fix a left point on the array, and for that keep extending the right endpoint, unless we exceed K. The number of times we can shift the right endpoint is the number of possible right endpoints if the left endpoint is fixed at the index where we had initially done. Now, just iterate over all possible left endpoints.

complexity: o(n^2).

A better solution would be to use a 2 pointer type algorithm. Here, observe that if we already have a subsegment whose product exceeds K, then if we multiply more elements, it will still always exceed K. Thus, we need to divide some previous elements first. So to do this, start the left and right endpoints at 0. Then keep moving the right endpoint and keep multiplying the new elements. Each time you are able to do so without exceeding K, increase ctr. Now, if the product exceeds K, then start shifting the left endpoint and divide the product that you had, with the element the left endpoint is processing, until the product again becomes lesser than K. Now, again start shifting the right endpoint and increasing ctr as before.

complexity: o(n) [since the right endpoint shifts at most n times and so does the left.]

→ Reply
»
7 years ago, # |
  Vote: I like it +4 Vote: I do not like it

Good day to you,

Well, since the K is pretty low, the easiest approach might (imho) be 2D Dynamic Programming, where first dimension is index of array and second is product. In each DP-state you either try to "multiply" by current number or simply go to next-number.

In recursive form, it might look like:

dyn (I k)
   if I == N: return 1
   if k >= K: return 0
   return dyn(I+1,k)+dyn(I+1,k*A[I])

I guess some memorisation + some modulo (etc.. sauce) will be necessary, yet I'm sure you'll deal with it.

Good Luck & Have Nice Day!

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    *memoization

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    can we do it by bottom up approach?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      For iterative approach, simply "reverse" what you are asking for:

      so instead of

      dyn(I+1,k)+dyn(I+1,k*A[I])

      you will iterate from back and ask for

      dp[I+1][k]+dp[I+1][k*A[I]]

      which is (as you can see) almost the same.

      The "ifs" ending the recursion can be done either by "pre-filling" of the table, yet in case of "multiplication" a would rather recommend to do them by ifs again.

      so basicaly it is same, yet instead if recursion, there is:

      for I (N → 1)
  for k (K → 1)
     dp[I+1][k]+dp[I+1][k*A[I]]
      → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +12 Vote: I do not like it

Let z be the number of zeros in the array and n be the total number of elements. There are (2z - 1)·2n - z subsequences with product 0. Remove all zeros now and operate on the remaining array.

We do something similar to what -Morass- described. Let small(i, j) denote the number of subsequences of the first i elements with product at most j. It's a simple DP, but we do this only for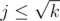 . Likewise, define large(i, j) such that the product is required to be at most . Again, we do this for .

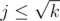It's easy to deduce the following formulas now:

The final answer large(n, 1) is obtained in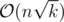 time.

I tried to implement this: Code. Just tested on your samples and only for small answers (no modulo).

→ Reply